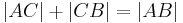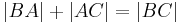Lösung von Aufgabe 5.2 S (SoSe 12): Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (→Lösung von H_2O) |
*m.g.* (Diskussion | Beiträge) (→Hinweise von M.G. zu LaTex) |
||
| (56 dazwischenliegende Versionen von 4 Benutzern werden nicht angezeigt) | |||
| Zeile 5: | Zeile 5: | ||
<br /> | <br /> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | ==Der Beweis als Video einer Studentin== | ||
| + | {{#ev:youtube|LCRLc6f2fPs}} | ||
===Hinweise von M.G. zu LaTex=== | ===Hinweise von M.G. zu LaTex=== | ||
Schön, dass Sie sich an die LaTex-Syntax herantrauen. Kleine Motivationshilfe: Sie können diese Syntax auch in den modernen Wordversionen und natürlich in Open Office verwenden. LaTex selbst ist ein Textsystem für mathematische Texte, das Freeware ist. In LaTex selbst wird der Beginn und das Ende einer mathematischen Formel durch das Dollarzeichen gekennzeichnet. Hier in der Wikiseitenbeschreibungssprache verwenden wir nicht das Dollarzeichen sondern die Tags <pre> <math> </math> </pre>. | Schön, dass Sie sich an die LaTex-Syntax herantrauen. Kleine Motivationshilfe: Sie können diese Syntax auch in den modernen Wordversionen und natürlich in Open Office verwenden. LaTex selbst ist ein Textsystem für mathematische Texte, das Freeware ist. In LaTex selbst wird der Beginn und das Ende einer mathematischen Formel durch das Dollarzeichen gekennzeichnet. Hier in der Wikiseitenbeschreibungssprache verwenden wir nicht das Dollarzeichen sondern die Tags <pre> <math> </math> </pre>. | ||
| Zeile 34: | Zeile 14: | ||
Wenn Sie irgend etwas Bestimmtes suchen können Sie auch googeln: | Wenn Sie irgend etwas Bestimmtes suchen können Sie auch googeln: | ||
| − | Nehmen wir an, Sie suchen das Zeichen für "für alle x": Geben Sie in Google die Suche "für alle x LaTex" ein und Sie sollten recht schnell fündig werden. | + | Nehmen wir an, Sie suchen das Zeichen für "für alle x": Geben Sie in Google die Suche "für alle x LaTex" ein und Sie sollten recht schnell fündig werden. |
===Hinweise von M.G. zu den Lösungsversuchen von RitterSport=== | ===Hinweise von M.G. zu den Lösungsversuchen von RitterSport=== | ||
| Zeile 143: | Zeile 123: | ||
<br />Aus <math> \operatorname{Zw} \left( A, B, C \right) </math> folgt <math> \operatorname{koll} \left( A, B, C \right)</math>.<br /> | <br />Aus <math> \operatorname{Zw} \left( A, B, C \right) </math> folgt <math> \operatorname{koll} \left( A, B, C \right)</math>.<br /> | ||
Die Entscheidende Begründung (innerhalb des realtiv kurzen Beweises) liegt im letzten Teil der Dreiecksungleichung: Zitat: "Ist umgekehrt eine dieser drei Gleichungen erfüllt, so sind A, B und C kollinear"<br />.--[[Benutzer:Buchner|Buchner]] 13:47, 24. Mai 2012 (CEST) | Die Entscheidende Begründung (innerhalb des realtiv kurzen Beweises) liegt im letzten Teil der Dreiecksungleichung: Zitat: "Ist umgekehrt eine dieser drei Gleichungen erfüllt, so sind A, B und C kollinear"<br />.--[[Benutzer:Buchner|Buchner]] 13:47, 24. Mai 2012 (CEST) | ||
| − | + | ===Lösung von H<sub>2</sub>O=== | |
| − | [[Datei:5.2.JPG]] | + | [[Datei:5.2.JPG]]<br /><br /> |
--[[Benutzer:Wurzel|H2O]] 20:06, 28. Mai 2012 (CEST) | --[[Benutzer:Wurzel|H2O]] 20:06, 28. Mai 2012 (CEST) | ||
| − | =====Kommentar M.G.===== | + | ====Kommentar M.G.==== |
| + | Wenn <math>|AB|+|BC|=|AC|</math> gilt, dann ist unmittelbar klar, dass <math>|AC|>|BC|</math> gilt. O.B.d.A. ist somit nicht angebracht. Die weiteren Beweischritte überzeugen dann allerdings nicht. | ||
| + | |||
| + | Zu zeigen ist: <math>\forall X \in \overline{AB}: X \in \overline{AC}</math>.<br /> | ||
| + | Annahme: nicht alle <math>X</math> der Strecke <math>\overline{AB}</math> gehören zu <math>\overline{AC}</math><br /> | ||
| + | also Annahme: Die Strecke <math>\overline{AB}</math> enthät einen Punkt <math>P</math>, der nicht zu <math>\overline{AC}</math>gehört:<br /> | ||
| + | <math>\exist P \in \overline{AB}: P \notin \overline{AC}</math><br /> | ||
| + | Wir übersetzen die Annahme: | ||
| + | Es gibt ein <math>P</math> auf <math>\overline{AB}</math> bedeutet: Es gibt ein <math>P</math>, für den die Gleichung<br /> | ||
| + | (I) <math>|AP|+|PB|=|AC|</math> gilt.<br /> | ||
| + | Der nicht zu <math>\overline{AC}</math> gehört:<br /> | ||
| + | (II) <math>|AP|+|PC|\not= |AC|</math> | ||
| + | |||
| + | Zusammen mit der Gleichung aus Schritt 2 Ihres Beweises sollte das Problem jetzt zu knacken sein. Viel Spaß dabei.--[[Benutzer:*m.g.*|*m.g.*]] 10:19, 29. Mai 2012 (CEST) | ||
| + | ===Lösungsversuch 2 von H<sub>2</sub>O=== | ||
| + | danke, somit zweiter Versuch<br /> | ||
| + | [[Datei:5.2.a.JPG]]<br /> | ||
| + | --[[Benutzer:Wurzel|H2O]] 19:43, 31. Mai 2012 (CEST) <br/> | ||
| + | ====Kommentar M.G.==== | ||
| + | =====Voraussetzung===== | ||
| + | <math>A \not= B \not= C \not= A</math> und <math>\operatorname{Zw}(A,B,C)</math> ist in Ordnung | ||
| + | =====Behauptung===== | ||
| + | <math>\overline{AB} \subset \overline{AC}</math> ist in Ordnung | ||
| + | =====Annahme===== | ||
| + | Es existiert <math>P \in \overline{AB}: P \not \in \overline{AC}</math> Der Beweis wird indirekt per Widerspruch geführt, ist so in Ordnung. | ||
| + | =====Beweisschritt 1===== | ||
| + | Wir berufen uns auf die Voraussetzung <math>\operatorname{Zw}(A,B,C)</math>, das dürfen wir und es ist auch sinnvoll das zu tun. | ||
| + | =====Beweisschritt 2===== | ||
| + | Aus (1) (wäre in der Begründung anzugeben) folgt entsprechend der Definition der Zwischenrelation die Gleichung <math>|AB|+|BC|=|AC|</math>. korrekt | ||
| + | =====Beweisschritt 3===== | ||
| + | Wir versuchen, die Annahme ins Spiel zu bringen. Das macht Sinn. Ich nehme an, den Schreibfehler haben Sie bereits gesehen. korrekt wäre: <math>\exist P \in \overline{AB}: P \not \in \overline{AC}</math> | ||
| + | =====Beweisschritt 4===== | ||
| + | Wenn die Annahme richtig wäre, könnte <math>P</math> nicht zwischen <math>A</math> und <math>C</math> liegen und damit würde die Gleichung <math>|AP|+|PC|=|AC|</math> nicht gelten, was, wie Sie es korrekt formuliert haben, <math>|AP|+|PC|\not=|AC|</math> bedeuten würde. | ||
| + | |||
| + | =====Beweisschritt 5===== | ||
| + | Jetzt wird es falsch. Schritt 4 lieferte uns <math>|AP|+|PC| \not= |AC|</math>. Demnach können 2 Fälle auftreten: entweder die linke Seite der Ungleichung ist größer als die rechte Seite der Ungleichung oder die linke Seite der Ungleichung ist kleiner als die rechte Seite der Ungleichung:<br /> | ||
| + | Fall 1: <math>|AP|+|PC| < |AC|</math><br /> | ||
| + | Fall 2: <math>|AP|+|PC| > |AC|</math><br /> | ||
| + | Sie betrachten nur Fall 1, diesen jedoch nicht korrekt. Wenn die Ungleichung <math>|AP|+|PC| \not= |AC|</math> gilt (und davon gehen wir bei unserem Widerspruchsbeweis ja aus) kann nicht der Fall <math>=</math> auftreten. Also einfach nur <math><</math> bzw. <math>></math>. | ||
| + | =====Beweisschritt 6===== | ||
| + | Sie untersuchen Fall 1: <math>|AP|+|PC| < |AC|</math>. <math>|AC|</math> wird entsprechend (2) durch <math>|AB|+|BC|</math> ersetzt, was uns <math>|AP|+|PB|<|AB|+|BC|</math> liefert. | ||
| + | =====Beweisschritt 7===== | ||
| + | Jetzt geht es durcheinander. Sie bringen <math>\operatorname{Zw}(A,P,B)</math> und <math>\operatorname{Zw}(A,B,C)</math> ins Spiel. Sie begründen mit der Definition der Zwischenrelation. Ich muss jetzt vermuten, warum Sie gerade jetzt auf <math>\operatorname{Zw}(A,P,B)</math> und <math>\operatorname{Zw}(A,B,C)</math> kommen. Ich habe den Verdacht, dass Sie das aus der linken und aus der rechten Seite der Ungleichung aus Schritt 7 schließen. Das wäre nicht korrekt. Allein aus der Aussageform <math>|AP|+|PB|</math> können Sie nicht auf <math>\operatorname{Zw}(A,P,B)</math> schließen. Dazu bedarf es einer Gleichung und nicht einer Ungleichung. Das Verrückte ist, dass Sie mit der Gültigkeit von <math>\operatorname{Zw}(A,P,B)</math> und <math>\operatorname{Zw}(A,B,C)</math> recht haben. <math>B</math> liegt nach Voraussetzung zwischen <math>A</math> und <math>C</math> und entsprechend unserer Annahme gehen wir davon aus, dass <math>P</math> ein Punkt der Strecke <math>\overline{AB}</math> ist und somit <math>\operatorname{Zw}(A,P,B)</math> gilt. Ich komme auf den Verdacht, dass Sie die Zwischenrelationen aus (6) ableiten, weil wir für die Gültigkeit der genannten Zwischenbeziehungen ja eigentlich keine Gleichung gebraucht hätten. Die Aussage von Schritt 7 hätten wir schon längst haben können. Es hätte nicht der Schritte (4), (5) und (6) bedurft. | ||
| + | |||
| + | =====Beweisschritt 8===== | ||
| + | Jetzt wird es definitiv falsch. Aus <math>\operatorname{Zw}(A,P,B)</math> und <math>\operatorname{Zw}(A,B,C)</math> kann auf keinen Fall <math>P=B</math> gefolgert werden. | ||
| + | =====Beweischritt 9===== | ||
| + | Wäre korrekt, wenn (8) korrekt wäre. (8) war aber leider nicht korrekt. | ||
| + | |||
| + | ===Lösung RitterSport=== | ||
| + | '''Meine Idee:<br/>''' | ||
| + | <u>Voraussetzung:</u> Zw(A,B,C), A n=B n=C n=A<br/> | ||
| + | <u>Behauptung:</u> Die Strecke AB ist eine echte Teilmenge von der Strecke AC<br/> | ||
| + | <u>Beweis:</u> | ||
| + | {| class="wikitable sortable" | ||
| + | !Nr||Beweisschritt!!Begründung | ||
| + | |- | ||
| + | | (1)|| Zw(A,B,C) || Voraussetzung | ||
| + | |- | ||
| + | | (2)|| |AB| + |BC| = |AC| || (1), Zw.-Rel. | ||
| + | |- | ||
| + | | (3)|| C Element AB+ || (1), Def. Halbgerade | ||
| + | |- | ||
| + | | (4) ||koll(A,B,C) || (2), II.3 | ||
| + | |} | ||
| + | <u>zu zeigen:</u> Alle x von <math>\overline{AB}</math> sind in <math>\overline{AC}</math> UND es existieren x in <math>\overline{AC}</math>, die nicht in <math>\overline{AB}</math> sind. <br/> | ||
| + | <br/> | ||
| + | <math>\overline{AB}</math> besteht aus den Punten A(Fall 1), B(Fall 2) und den Punten zwischen A und B(Fall 3).<br/> | ||
| + | Nun muss ich zeigen, dass alle 3 Fälle auch in <math>\overline{AC}</math> liegen. <br/> | ||
| + | <br/> | ||
| + | Fall 1: A gehört zu <math>\overline{AC}</math>(trivial), weil <math>\overline{AC}</math> definiert ist als: <math>\overline{AC}</math>={P\AB+BC=AC} (2)<br/> | ||
| + | Fall 2: B gehört zu <math>\overline{AC}</math>, da koll(A,B,C)(3) und Zw(A,B,C)(1)<br/> | ||
| + | Fall 3: Zw(A,X,B) gehört zu <math>\overline{AC}</math> weil wir das gleich im Widerspruchsbeweis zeigen.<br/> | ||
| + | |||
| + | Wir wollen zeigen, dass X nicht nur zwischen A und B liegt, sondern auch zwischen A und C. | ||
| + | Wenn wir zeigen können, dass koll(A,X,C) gilt, wissen wir, dass eine Zwischenreation gilt. | ||
| + | |||
| + | |||
| + | {| class="wikitable sortable" | ||
| + | !Überschrift 1!!Überschrift 2 | ||
| + | |- | ||
| + | | (3.1): koll(A,B,C) || (4) | ||
| + | |- | ||
| + | | (3.2): Zw(A,X,B) || Fall 3 | ||
| + | |- | ||
| + | | (3.3): X Element AB+ || (3.2) | ||
| + | |- | ||
| + | | (3.4): koll(A,X,B) || (3.2), Dreiecksungleichung | ||
| + | |- | ||
| + | | (3.5): koll(A,X,C) || (3.1), (3.4) <span style="color: red">darf man das?</span> | ||
| + | |- | ||
| + | | (3.6): Zw(A,X,C) v Zw(X,A,C) v Zw(A,C,X) || (3.5), Dreiecksungleichung | ||
| + | |- | ||
| + | |} | ||
| + | <br /> | ||
| + | Mind. eine der 3 Zwischenrelationen muss gelten. <br /> | ||
| + | Nun zeige ich noch, dass 2 der 3 Zwischenrelationen nicht gelten und weiß somit, dass die 3. gilt.<br/> | ||
| + | <span style="color: red">Da X Element von <math>\overline{AC}</math> sein muss, fallen doch Zw(X,A,C) und Zw(A,C,X) weg. Für was brauche ich dann noch die beiden Annahmen?</span> | ||
| + | |||
| + | <u>Annahme 1:</u> Zw(X,A,C)<br /> | ||
| + | Widerspruch zu (3.3 --> X Element AB+)<br /> | ||
| + | und: Dann ist X nicht mehr Element <math>\overline{AC}</math><br /> | ||
| + | <u>Annahme 2:</u> Zw(A,C,X)<br /> | ||
| + | Dann ist X nicht mehr Element <math>\overline{AC}</math><br /> | ||
| + | <br /> | ||
| + | Je länger ich über den Beweis nachdenke, desto unzufriedener werde ich.<br /> | ||
| + | Ich nehme an, dass ich Annahme 1 und 2 nicht so begründen darf.<br /> | ||
| + | Könnte mir nochmal jemand einen Tip geben?<br /> | ||
| + | <br /> | ||
| + | ===Anmerkungen von Buchner zur Lösung von RitterSport=== | ||
| + | Ihre Vorgehensweise gefällt mir sehr gut und alles ist gut nachvollziehbar und gut begründet. Gehen wir den Beweis mal Schritt für Schritt durch.<br /><br /> | ||
| + | '''Obere Tabelle''': Gute Idee- Sie schreiben alles auf, was Sie aus der Voraussetzung schonmal folgern können. (3) müssen Sie etwas anders begründen. Dass <math>C \in \ AB^{+} </math> gilt wegen (1) und der Definition von Halbgerade. Ansonsten Super!<br /><br /> | ||
| + | Sehr schön, wie sie das zu zeigende nochmal ausformuliert haben! Fallunterscheidung auch gut- aber Achtung: Bei '''Fall drei''' müssen sie nicht zeigen, dass Zw(A,X,B) gilt. Das ist ihre Annahme für Fall drei, d.h. das steht hier fest. Zu zeigen ist für Fall drei, dass <math>X \in\overline{AC}</math>, d.h. dass <math>\operatorname(Zw)(A,X,C)</math> gilt.<br /><br /> | ||
| + | Ihre Idee eines Widerspruchsbeweises ist gut. Also:<br /> | ||
| + | '''Fall drei:'''<br /> | ||
| + | Vor:<math>\operatorname(Zw)(A,X,B)</math> (und zusätzlich alles aus der obersten Tabelle)<br /> | ||
| + | Beh: <math>\operatorname(Zw)(A,X,C)</math> und somit <math>X \in\overline{AC}</math>.<br /><br /> | ||
| + | |||
| + | a) Zunächst müssen wir zeigen, dass <math>\operatorname{koll}(A, X, C) </math>, denn dann wissen wir, dass genau eine der Zwischenrealtionen gilt.<br /> | ||
| + | b) Anschließend führen wir die beiden Zwischenrealtionen <math>\operatorname(Zw)(A,C,X)</math> und <math>\operatorname(Zw)(X,A,C)</math> zum Widerspruch.<br /><br /> | ||
| + | Können Sie hier weitermachen?<br /> | ||
| + | --[[Benutzer:Buchner|Buchner]] 11:35, 11. Jun. 2012 (CEST)<br/> | ||
| + | Vielen Dank für Ihre Rückmeldung.<br/> | ||
| + | Ich versuche mein Glück und überarbeite das Fehlerhafte nochmal.<br/> | ||
| + | <blockquote style="border: 1px solid blue; padding: 2em;"> | ||
| + | |||
| + | Hier mal der Beweis auf einer Seite. Passt das?<br/> | ||
| + | [[[Datei:[Datei:<document>RitterSport_IMG_0002.pdf</document>]]]] | ||
| + | </blockquote> | ||
Aktuelle Version vom 24. Juni 2012, 20:47 Uhr
Zeigen Sie, dass für drei paarweise verschiedene Punkte  und
und  gilt:
gilt:





Tipps zu Aufgabe 5.2 (SoSe_12)
Inhaltsverzeichnis |
Der Beweis als Video einer Studentin
Hinweise von M.G. zu LaTex
Schön, dass Sie sich an die LaTex-Syntax herantrauen. Kleine Motivationshilfe: Sie können diese Syntax auch in den modernen Wordversionen und natürlich in Open Office verwenden. LaTex selbst ist ein Textsystem für mathematische Texte, das Freeware ist. In LaTex selbst wird der Beginn und das Ende einer mathematischen Formel durch das Dollarzeichen gekennzeichnet. Hier in der Wikiseitenbeschreibungssprache verwenden wir nicht das Dollarzeichen sondern die Tags<math> </math>.
Eine umfassende Hilfe zu LaTex im Rahmen des Wikis finden sie hier [1]
Wenn Sie irgend etwas Bestimmtes suchen können Sie auch googeln: Nehmen wir an, Sie suchen das Zeichen für "für alle x": Geben Sie in Google die Suche "für alle x LaTex" ein und Sie sollten recht schnell fündig werden.
Hinweise von M.G. zu den Lösungsversuchen von RitterSport
Irgendwie scheinen Sie selbst noch nicht ganz überzeugt von Ihren Beweisen. Sie müssen die im übrigen nicht so formal schreiben, sie dürfen auch textliche Sätze (o-Ton von meinem ehemaligen Chemielehrer) verwenden.
Also ich versuche es mal:
Es seien 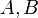 und
und  drei paarweise verschiedene Punkte, von denen der Punkt
drei paarweise verschiedene Punkte, von denen der Punkt  zwischen den beiden anderen Punkten, also
zwischen den beiden anderen Punkten, also  und
und  , liegt.
, liegt.
Zeigen sollen wir, dass nun die Strecke  eine Teilmenge der Strecke
eine Teilmenge der Strecke  ist.
ist.
Dieses hätten wir gezeigt, wenn wir nachgewiesen hätten, dass jeder Punkt von .... auch ein Punkt ..... (ergänzen Sie selbst.)
Es sei nun  ein beliebiger Punkt der Strecke
ein beliebiger Punkt der Strecke  .
.
Weil  zur Strecke
zur Strecke  gehört, liegt er entsprechend der Definition des Begriffs Strecke zwischen den beiden Punkten .... (ergänzen Sie wieder selbst)
gehört, liegt er entsprechend der Definition des Begriffs Strecke zwischen den beiden Punkten .... (ergänzen Sie wieder selbst)
Da nun der Punkt  zwischen den Punkten .... liegt, gilt entsprechend der Definition der Zwischenrelation die folgende Gleichung:
zwischen den Punkten .... liegt, gilt entsprechend der Definition der Zwischenrelation die folgende Gleichung:
....
Zeigen wollen wir, das  auch zwischen .... liegt.
auch zwischen .... liegt.
Entsprechend der Definition der Zwischenrelation wäre letzteres der Fall, wenn die Gleichung ... gelten würde.
Für den Nachweis der Gültigkeit der obigen Gleichung dürfen wir die Voraussetzung, dass  zwischen
zwischen  und
und  liegt verwenden. Als Gleichung ausgedrückt stellt sich diese Voraussetzung wie folgt dar: ....
liegt verwenden. Als Gleichung ausgedrückt stellt sich diese Voraussetzung wie folgt dar: ....
Jetzt haben Sie zwei Gleichungen, von denen Sie ausgehen dürfen und eine deren Gültigkeit Sie nachweisen müssen. Wenn Sie wissen, welche Gleichungen das sind, sollte der Beweis kein Problem mehr sein. Viel Erfolg! --*m.g.* 17:55, 20. Mai 2012 (CEST)
Lösungsvorschlag (oz44oz)
--Oz44oz 17:58, 21. Mai 2012 (CEST)
Frage zum Lösungsvorschlag von H20
--Kopernikus 18:40, 22. Mai 2012 (CEST)
Ich weiß nicht, ob deine Vorraussetzung so richtig ist
Ich glaube da geht ein Teil der Vorraussetzung frend mit der Behauptung.
Was mir noch aufgefallen ist und über was ich mir auch den Kopf zerbrochen hab ist, ob man irg. sagen kann, dass koll(ABC)
In der Aufgabe steht das nicht. Es steht da, sie sind paarweise verschieden und zw(ABC).
Ich hab das mal rausgeschrieben, was meiner Meinung nach dafür notwendig wäre. Jedoch bin ich immer wieder in die Schranken gewiesen worden. :-(
Einfach zu sagen sie sind halt koll geht glaube ich nicht.
Definition I/2: (kollinear)
- Eine Menge von Punkten heißt kollinear, wenn es eine Gerade gibt, die alle Punkte der Menge enthält.
- Schreibweise: koll(A, B, C, ...) Sollten die Punkte A, B, C einer Menge nicht kollinear sein, so schreibt man:nkoll(A, B, C)
es wird in der Def. kollinear von einer Geraden, nicht von einer Stecke gesprochen. Ich weiß leider noch zu wenig über die Strecke. Ich weiß nichtmal, dass die ein Teil einer Geraden sein könnte.
Axiom II/3: (Dreiecksungleichung)
- Für drei beliebige Punkte
 und
und  gilt:
gilt: 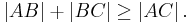
- Für drei beliebige Punkte
- Falls
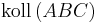 , dann ist eine der folgenden Gleichungen erfüllt:
, dann ist eine der folgenden Gleichungen erfüllt:
- Falls
- Ist umgekehrt eine dieser drei Gleichungen erfüllt, so sind
 ,
,  und
und  kollinear.
kollinear.
ich kann nicht sagen Sie sind kollinear, wenn ich nicht weis, ob
Definition II.2: (Zwischenrelation)
- Ein Punkt
 liegt zwischen zwei Punkten
liegt zwischen zwei Punkten  und
und  , wenn gilt:
, wenn gilt:
- Ein Punkt
-
 und
und
 ,
,  und
und  sind paarweise verschieden.
sind paarweise verschieden.
-
- Schreibweise:
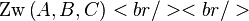 sagt nichts über kollinear
sagt nichts über kollinear
- Schreibweise:
Definition II/3 "Vorschlag Kopernikus" Def. Strecke)
- Die Strecke
 ist die Menge aller Punkte, die vereinigt mit A und B zwischen A und B liegen.--Kopernikus 15:52, 22. Mai 2012 (CEST)
ist die Menge aller Punkte, die vereinigt mit A und B zwischen A und B liegen.--Kopernikus 15:52, 22. Mai 2012 (CEST)
sagt auch nnichts über kollinear.
- Die Strecke
Ich finde deshalb oz44oz Lösung sehr gut und denke auch, dass diese so richtig ist. :-)
--Kopernikus 18:39, 22. Mai 2012 (CEST)
Anmerkungen von Buchner zu Lösungsvorschlag (oz44oz) und Diskussion
Sie führen eine sehr gute Diskussion. Zunächst dazu, ob aus 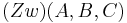 gefolgert werden kann, dass gilt
gefolgert werden kann, dass gilt 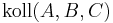 . Die Antwort ist: Ja. Sie können den Satz
. Die Antwort ist: Ja. Sie können den Satz
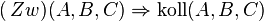 leicht beweisen. Tipp: Schauen Sie das Axiom Dreiecksungleichung nochmal genau an!
leicht beweisen. Tipp: Schauen Sie das Axiom Dreiecksungleichung nochmal genau an!
Die Lösung von oz44oz fängt sehr gut an und ist gut aufgeschrieben. Ich sehe aber ein Problem: Wie können Sie aus Schritt 5 den Schritt 6 begründen? Sie stecken hier ziemlich viel "Hintergrundwissen" rein, was Sie aus der Anschauung gewinnen, also z.B. aus einer Skizze. Für einen formalen Beweis reicht das leider nicht.
Also konkret: Sie behaupten in Schritt 5 und 6 einfach, dass 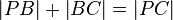 ist. Warum sollte das so sein? Wenn Sie es hier schaffen, sauber zu begründen (d.h. die fehlenden Beweis- und Begründungsschritte einzufügen), sind wir ein gutes Stück weiter.
ist. Warum sollte das so sein? Wenn Sie es hier schaffen, sauber zu begründen (d.h. die fehlenden Beweis- und Begründungsschritte einzufügen), sind wir ein gutes Stück weiter.
Frage an Fr. Buchner
"Die Antwort ist: Ja. Sie können den Satz
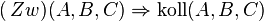 leicht beweisen.
leicht beweisen.
Vielleicht hat man mich falsch verstanden." Ich kann doch nur weil ich was vielleicht beweisen darf einfach so annehmen und mit dazu in die Vor. stecken ...oder doch??? Und wenn nicht muss ich das sagen, dass ich die wegen des Satzes weiß.--Kopernikus 17:02, 23. Mai 2012 (CEST)
Satz II.2:
- Aus
 folgt
folgt  .
.
- Aus
Ist trivial....der Leser überzeugt sich davon...
Aber ich würde es auf jedenfall vermerken, dass ich mich auf den Satz berufe....die Frage ist jedoch, darf ich was annehmen, nur weil es trivial ist? Wo ziehe ich die Grenze was trivial ist und was nicht? Zitat aus der Vorlesung von m.g. in seinem Studium war viel trivial was nicht gleich ersichtlich ist." Ich brauche ein Axiom um zu zweigen, dass für :Für zwei beliebige Punkte  und
und  gilt
gilt 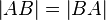 . das ist für mich auch trivial.--Kopernikus 17:29, 23. Mai 2012 (CEST)
. das ist für mich auch trivial.--Kopernikus 17:29, 23. Mai 2012 (CEST)
Antwort an Kopernikus
Ich gebe Ihnen Recht- Wenn "trivial" als Beweis für einen Satz steht, ist das nicht zufriedenstellend. Aber trivial bedeutet, dass man es ganz leicht beweisen kann- im Gegensatz zu einem Axiom. 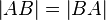 können Sie nicht beweisen, deshalb müssen wir es axiomatisch fordern.
können Sie nicht beweisen, deshalb müssen wir es axiomatisch fordern.
Sowohl Axiome als auch Sätze können leicht ersichtlich sein- der Unterschied ist, dass wir Axiome nicht beweisen können und Sätze beweisen müssen.
Ich gebe Ihnen einen Tipp für den Satz
Aus  folgt
folgt 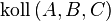 .
.
Die Entscheidende Begründung (innerhalb des realtiv kurzen Beweises) liegt im letzten Teil der Dreiecksungleichung: Zitat: "Ist umgekehrt eine dieser drei Gleichungen erfüllt, so sind A, B und C kollinear"
.--Buchner 13:47, 24. Mai 2012 (CEST)
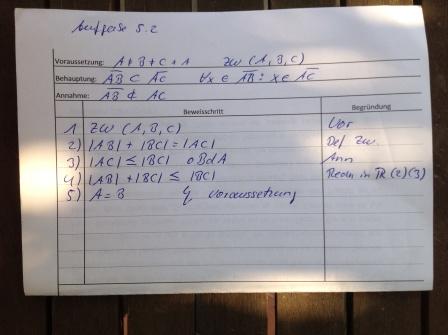
Lösung von H2O
--H2O 20:06, 28. Mai 2012 (CEST)
Kommentar M.G.
Wenn 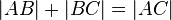 gilt, dann ist unmittelbar klar, dass
gilt, dann ist unmittelbar klar, dass 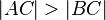 gilt. O.B.d.A. ist somit nicht angebracht. Die weiteren Beweischritte überzeugen dann allerdings nicht.
gilt. O.B.d.A. ist somit nicht angebracht. Die weiteren Beweischritte überzeugen dann allerdings nicht.
Zu zeigen ist: 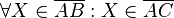 .
.
Annahme: nicht alle 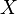 der Strecke
der Strecke  gehören zu
gehören zu 
also Annahme: Die Strecke  enthät einen Punkt
enthät einen Punkt  , der nicht zu
, der nicht zu  gehört:
gehört:
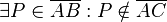
Wir übersetzen die Annahme:
Es gibt ein  auf
auf  bedeutet: Es gibt ein
bedeutet: Es gibt ein  , für den die Gleichung
, für den die Gleichung
(I) 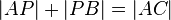 gilt.
gilt.
Der nicht zu  gehört:
gehört:
(II) 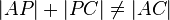
Zusammen mit der Gleichung aus Schritt 2 Ihres Beweises sollte das Problem jetzt zu knacken sein. Viel Spaß dabei.--*m.g.* 10:19, 29. Mai 2012 (CEST)
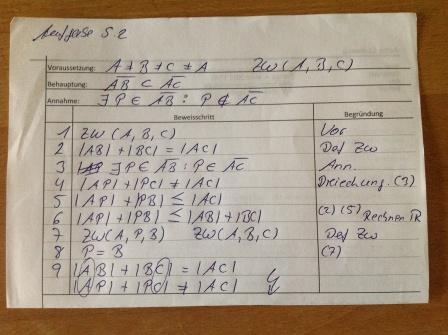
Lösungsversuch 2 von H2O
danke, somit zweiter Versuch
--H2O 19:43, 31. Mai 2012 (CEST)
Kommentar M.G.
Voraussetzung
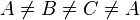 und
und 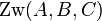 ist in Ordnung
ist in Ordnung
Behauptung
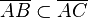 ist in Ordnung
ist in Ordnung
Annahme
Es existiert 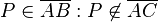 Der Beweis wird indirekt per Widerspruch geführt, ist so in Ordnung.
Der Beweis wird indirekt per Widerspruch geführt, ist so in Ordnung.
Beweisschritt 1
Wir berufen uns auf die Voraussetzung 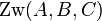 , das dürfen wir und es ist auch sinnvoll das zu tun.
, das dürfen wir und es ist auch sinnvoll das zu tun.
Beweisschritt 2
Aus (1) (wäre in der Begründung anzugeben) folgt entsprechend der Definition der Zwischenrelation die Gleichung 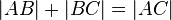 . korrekt
. korrekt
Beweisschritt 3
Wir versuchen, die Annahme ins Spiel zu bringen. Das macht Sinn. Ich nehme an, den Schreibfehler haben Sie bereits gesehen. korrekt wäre: 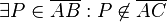
Beweisschritt 4
Wenn die Annahme richtig wäre, könnte  nicht zwischen
nicht zwischen  und
und  liegen und damit würde die Gleichung
liegen und damit würde die Gleichung 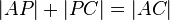 nicht gelten, was, wie Sie es korrekt formuliert haben,
nicht gelten, was, wie Sie es korrekt formuliert haben, 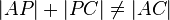 bedeuten würde.
bedeuten würde.
Beweisschritt 5
Jetzt wird es falsch. Schritt 4 lieferte uns 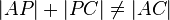 . Demnach können 2 Fälle auftreten: entweder die linke Seite der Ungleichung ist größer als die rechte Seite der Ungleichung oder die linke Seite der Ungleichung ist kleiner als die rechte Seite der Ungleichung:
. Demnach können 2 Fälle auftreten: entweder die linke Seite der Ungleichung ist größer als die rechte Seite der Ungleichung oder die linke Seite der Ungleichung ist kleiner als die rechte Seite der Ungleichung:
Fall 1: 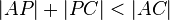
Fall 2: 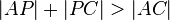
Sie betrachten nur Fall 1, diesen jedoch nicht korrekt. Wenn die Ungleichung 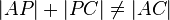 gilt (und davon gehen wir bei unserem Widerspruchsbeweis ja aus) kann nicht der Fall
gilt (und davon gehen wir bei unserem Widerspruchsbeweis ja aus) kann nicht der Fall  auftreten. Also einfach nur
auftreten. Also einfach nur 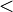 bzw.
bzw. 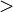 .
.
Beweisschritt 6
Sie untersuchen Fall 1: 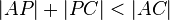 .
. 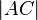 wird entsprechend (2) durch
wird entsprechend (2) durch 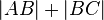 ersetzt, was uns
ersetzt, was uns 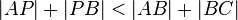 liefert.
liefert.
Beweisschritt 7
Jetzt geht es durcheinander. Sie bringen 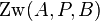 und
und 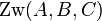 ins Spiel. Sie begründen mit der Definition der Zwischenrelation. Ich muss jetzt vermuten, warum Sie gerade jetzt auf
ins Spiel. Sie begründen mit der Definition der Zwischenrelation. Ich muss jetzt vermuten, warum Sie gerade jetzt auf 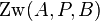 und
und 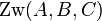 kommen. Ich habe den Verdacht, dass Sie das aus der linken und aus der rechten Seite der Ungleichung aus Schritt 7 schließen. Das wäre nicht korrekt. Allein aus der Aussageform
kommen. Ich habe den Verdacht, dass Sie das aus der linken und aus der rechten Seite der Ungleichung aus Schritt 7 schließen. Das wäre nicht korrekt. Allein aus der Aussageform 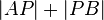 können Sie nicht auf
können Sie nicht auf 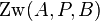 schließen. Dazu bedarf es einer Gleichung und nicht einer Ungleichung. Das Verrückte ist, dass Sie mit der Gültigkeit von
schließen. Dazu bedarf es einer Gleichung und nicht einer Ungleichung. Das Verrückte ist, dass Sie mit der Gültigkeit von 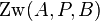 und
und 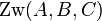 recht haben.
recht haben.  liegt nach Voraussetzung zwischen
liegt nach Voraussetzung zwischen  und
und  und entsprechend unserer Annahme gehen wir davon aus, dass
und entsprechend unserer Annahme gehen wir davon aus, dass  ein Punkt der Strecke
ein Punkt der Strecke  ist und somit
ist und somit 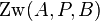 gilt. Ich komme auf den Verdacht, dass Sie die Zwischenrelationen aus (6) ableiten, weil wir für die Gültigkeit der genannten Zwischenbeziehungen ja eigentlich keine Gleichung gebraucht hätten. Die Aussage von Schritt 7 hätten wir schon längst haben können. Es hätte nicht der Schritte (4), (5) und (6) bedurft.
gilt. Ich komme auf den Verdacht, dass Sie die Zwischenrelationen aus (6) ableiten, weil wir für die Gültigkeit der genannten Zwischenbeziehungen ja eigentlich keine Gleichung gebraucht hätten. Die Aussage von Schritt 7 hätten wir schon längst haben können. Es hätte nicht der Schritte (4), (5) und (6) bedurft.
Beweisschritt 8
Jetzt wird es definitiv falsch. Aus 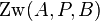 und
und 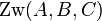 kann auf keinen Fall
kann auf keinen Fall 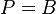 gefolgert werden.
gefolgert werden.
Beweischritt 9
Wäre korrekt, wenn (8) korrekt wäre. (8) war aber leider nicht korrekt.
Lösung RitterSport
Meine Idee:
Voraussetzung: Zw(A,B,C), A n=B n=C n=A
Behauptung: Die Strecke AB ist eine echte Teilmenge von der Strecke AC
Beweis:
| Nr | Beweisschritt | Begründung |
|---|---|---|
| (1) | Zw(A,B,C) | Voraussetzung |
| (2) | AB| + |BC| = |AC| | (1), Zw.-Rel. |
| (3) | C Element AB+ | (1), Def. Halbgerade |
| (4) | koll(A,B,C) | (2), II.3 |
zu zeigen: Alle x von  sind in
sind in  UND es existieren x in
UND es existieren x in  , die nicht in
, die nicht in  sind.
sind.
 besteht aus den Punten A(Fall 1), B(Fall 2) und den Punten zwischen A und B(Fall 3).
besteht aus den Punten A(Fall 1), B(Fall 2) und den Punten zwischen A und B(Fall 3).
Nun muss ich zeigen, dass alle 3 Fälle auch in  liegen.
liegen.
Fall 1: A gehört zu  (trivial), weil
(trivial), weil  definiert ist als:
definiert ist als:  ={P\AB+BC=AC} (2)
={P\AB+BC=AC} (2)
Fall 2: B gehört zu  , da koll(A,B,C)(3) und Zw(A,B,C)(1)
, da koll(A,B,C)(3) und Zw(A,B,C)(1)
Fall 3: Zw(A,X,B) gehört zu  weil wir das gleich im Widerspruchsbeweis zeigen.
weil wir das gleich im Widerspruchsbeweis zeigen.
Wir wollen zeigen, dass X nicht nur zwischen A und B liegt, sondern auch zwischen A und C. Wenn wir zeigen können, dass koll(A,X,C) gilt, wissen wir, dass eine Zwischenreation gilt.
| Überschrift 1 | Überschrift 2 |
|---|---|
| (3.1): koll(A,B,C) | (4) |
| (3.2): Zw(A,X,B) | Fall 3 |
| (3.3): X Element AB+ | (3.2) |
| (3.4): koll(A,X,B) | (3.2), Dreiecksungleichung |
| (3.5): koll(A,X,C) | (3.1), (3.4) darf man das? |
| (3.6): Zw(A,X,C) v Zw(X,A,C) v Zw(A,C,X) | (3.5), Dreiecksungleichung |
Mind. eine der 3 Zwischenrelationen muss gelten.
Nun zeige ich noch, dass 2 der 3 Zwischenrelationen nicht gelten und weiß somit, dass die 3. gilt.
Da X Element von  sein muss, fallen doch Zw(X,A,C) und Zw(A,C,X) weg. Für was brauche ich dann noch die beiden Annahmen?
sein muss, fallen doch Zw(X,A,C) und Zw(A,C,X) weg. Für was brauche ich dann noch die beiden Annahmen?
Annahme 1: Zw(X,A,C)
Widerspruch zu (3.3 --> X Element AB+)
und: Dann ist X nicht mehr Element 
Annahme 2: Zw(A,C,X)
Dann ist X nicht mehr Element 
Je länger ich über den Beweis nachdenke, desto unzufriedener werde ich.
Ich nehme an, dass ich Annahme 1 und 2 nicht so begründen darf.
Könnte mir nochmal jemand einen Tip geben?
Anmerkungen von Buchner zur Lösung von RitterSport
Ihre Vorgehensweise gefällt mir sehr gut und alles ist gut nachvollziehbar und gut begründet. Gehen wir den Beweis mal Schritt für Schritt durch.
Obere Tabelle: Gute Idee- Sie schreiben alles auf, was Sie aus der Voraussetzung schonmal folgern können. (3) müssen Sie etwas anders begründen. Dass 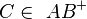 gilt wegen (1) und der Definition von Halbgerade. Ansonsten Super!
gilt wegen (1) und der Definition von Halbgerade. Ansonsten Super!
Sehr schön, wie sie das zu zeigende nochmal ausformuliert haben! Fallunterscheidung auch gut- aber Achtung: Bei Fall drei müssen sie nicht zeigen, dass Zw(A,X,B) gilt. Das ist ihre Annahme für Fall drei, d.h. das steht hier fest. Zu zeigen ist für Fall drei, dass  , d.h. dass
, d.h. dass 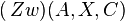 gilt.
gilt.
Ihre Idee eines Widerspruchsbeweises ist gut. Also:
Fall drei:
Vor: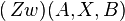 (und zusätzlich alles aus der obersten Tabelle)
(und zusätzlich alles aus der obersten Tabelle)
Beh: 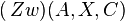 und somit
und somit  .
.
a) Zunächst müssen wir zeigen, dass 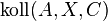 , denn dann wissen wir, dass genau eine der Zwischenrealtionen gilt.
, denn dann wissen wir, dass genau eine der Zwischenrealtionen gilt.
b) Anschließend führen wir die beiden Zwischenrealtionen 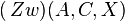 und
und 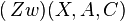 zum Widerspruch.
zum Widerspruch.
Können Sie hier weitermachen?
--Buchner 11:35, 11. Jun. 2012 (CEST)
Vielen Dank für Ihre Rückmeldung.
Ich versuche mein Glück und überarbeite das Fehlerhafte nochmal.
Hier mal der Beweis auf einer Seite. Passt das?
[[[Datei:[Datei:<document>RitterSport_IMG_0002.pdf</document>]]]]