Begriff der Strecke, verschiedene Definitionsversuche SoSe 12: Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (→Definition II.4: (Länge einer Strecke)) |
*m.g.* (Diskussion | Beiträge) (→Bemerkung M.G.) |
||
| (4 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 46: | Zeile 46: | ||
== Definition II.4: (Länge einer Strecke) == | == Definition II.4: (Länge einer Strecke) == | ||
::Es seien <math>\ A</math> und <math>\ B</math> zwei verschiedene Punkte. ... (ergänzen Sie) | ::Es seien <math>\ A</math> und <math>\ B</math> zwei verschiedene Punkte. ... (ergänzen Sie) | ||
| − | ===Version von === | + | ===Version von jaegert01=== |
| − | + | ====Vorschlag: Definition II.4: (Länge einer Strecke)==== | |
::Es seien <math>\ A</math> und <math>\ B</math> zwei verschiedene Punkte. Wenn <math>\ A</math> und <math>\ B</math> die Endpunkte der Strecke <math>\overline{AB} </math> sind, so ist ihr Abstand <math>\ d </math> zueinander die Länge <math> \left| AB \right|</math> der Strecke <math>\overline{AB} </math> . --[[Benutzer:jaegert01|jaegert01]] 12:06, 25. Mai 2012 (CEST) | ::Es seien <math>\ A</math> und <math>\ B</math> zwei verschiedene Punkte. Wenn <math>\ A</math> und <math>\ B</math> die Endpunkte der Strecke <math>\overline{AB} </math> sind, so ist ihr Abstand <math>\ d </math> zueinander die Länge <math> \left| AB \right|</math> der Strecke <math>\overline{AB} </math> . --[[Benutzer:jaegert01|jaegert01]] 12:06, 25. Mai 2012 (CEST) | ||
<br /><br /> | <br /><br /> | ||
| − | |||
| − | |||
| − | |||
===== Zum Vorschlag von jaegert01: Definition II.4: (Länge einer Strecke) ===== | ===== Zum Vorschlag von jaegert01: Definition II.4: (Länge einer Strecke) ===== | ||
Inhaltlich absolut richtig- sprachlich noch etwas zu holprig... Einfach nochmal versuchen!--[[Benutzer:Buchner|Buchner]] 16:22, 31. Mai 2012 (CEST) | Inhaltlich absolut richtig- sprachlich noch etwas zu holprig... Einfach nochmal versuchen!--[[Benutzer:Buchner|Buchner]] 16:22, 31. Mai 2012 (CEST) | ||
| + | |||
| + | ===Version von Numero6 alias Tchu Tcha Tcha=== | ||
| + | ====Vorschlag 2: Definition II.4: (Länge einer Strecke''')==== | ||
| + | ::Es seien <math>\ A</math> und <math>\ B</math> zwei verschiedene Punkte. Wenn <math>\ A</math> und <math>\ B</math> die Endpunkte der Strecke <math>\overline{AB} </math> sind, dann ist die Länge einer Strecke <math>\overline{AB}</math> die Zahl (d), die nach dem Abstandsaxiom den Punkten A und B zugeordnet werden kann.<br />d=<math>\left| AB \right|</math> <br />--[[Benutzer:Nummero6|Tchu Tcha Tcha]] 12:31, 3. Jun. 2012 (CEST) | ||
| + | ====Bemerkung M.G.==== | ||
| + | ::Das kommt ein wenig flüssiger rüber als die Version von jaegert01. Nur mit der Formulierung <blockquote style="border: 1px solid blue; padding: 2em;">Wenn <math>A</math> und <math>B</math> die Endpunkte der Strecke <math>\overline{AB} </math> sind, ...</blockquote><br /> | ||
| + | ::tue ich mich etwas schwer. Es ist doch wohl immer so, dass die Punkte <math>A</math> und <math> B</math> die Endpunkte der Strecke <math>\overline{AB}</math> sind.--[[Benutzer:*m.g.*|*m.g.*]] 16:14, 3. Jun. 2012 (CEST) | ||
<!--- Was hier drunter steht muss stehen bleiben ---> | <!--- Was hier drunter steht muss stehen bleiben ---> | ||
Aktuelle Version vom 3. Juni 2012, 15:16 Uhr
|
Der Begriff der StreckeDefinition II.3: (Strecke, Endpunkte einer Strecke)
Definition II.3 - (1. Vorschlag Kopernikus Strecke, der Endpunkte)
Anmerkung von Buchner zur Definition von Kopernikus
Definition II.3 - (Vorschlag Kopernikus zweiter Versuch)(2.1 Vorschlag Kopernikus Strecke)
(2.2 Vorschlag Kopernikus Endpunkte)
Anmerkung von Buchner zu Definition II.3 - (Vorschlag Kopernikus zweiter Versuch)Ihr letzter Vorschlag gefällt mir am besten - man würde die Endpunkte nicht seperat definieren, sondern wie Sie es hier gemacht haben zur Definition der Strecke dazuschreiben. Der erste Satz ist noch etwas ungewöhnlich formuliert (was heißt "vereinigt mit A und B zwischen A und B?). Besser: Definition II.3 (Strecke, Endpunkte einer Strecke)
Einfacher ist die formale Schreibweise:
--Buchner 17:13, 23. Mai 2012 (CEST) Definition II.4: (Länge einer Strecke)
Version von jaegert01Vorschlag: Definition II.4: (Länge einer Strecke)
Zum Vorschlag von jaegert01: Definition II.4: (Länge einer Strecke)Inhaltlich absolut richtig- sprachlich noch etwas zu holprig... Einfach nochmal versuchen!--Buchner 16:22, 31. Mai 2012 (CEST) Version von Numero6 alias Tchu Tcha TchaVorschlag 2: Definition II.4: (Länge einer Strecke)
Bemerkung M.G.
|
 und
und  zwei verschiedene Punkte. ... (ergänzen Sie)
zwei verschiedene Punkte. ... (ergänzen Sie)
 ist...")--
ist...")-- und
und  zwei verschiedene Punkte. Unter der Strecke
zwei verschiedene Punkte. Unter der Strecke 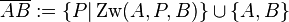 . A und B heißen Endpunkte der Strecke
. A und B heißen Endpunkte der Strecke 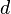 zueinander die Länge
zueinander die Länge  der Strecke
der Strecke 
