Winkelmessung SS 2012: Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (→Das Winkelmaßaxiom) |
(→Definition V.10: (senkrecht für Strecken)) |
||
| (39 dazwischenliegende Versionen von 5 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| + | <div style="margin:0; margin-right:4px; border:1px solid #27408B; padding: 1em 1em 1em 1em; background-color:#FFFF99; align:left;"> | ||
| + | {|width=90%| style="background-color:#FFFF99; padding:1em" | ||
| + | | valign="top" | | ||
| + | |||
| + | <!--- ------------------------------------------------------------------------------------------ ---> | ||
| + | |||
== Das Winkelmaß == | == Das Winkelmaß == | ||
=== Was bedeutet es, die Größe eines Winkels zu messen? === | === Was bedeutet es, die Größe eines Winkels zu messen? === | ||
| Zeile 19: | Zeile 25: | ||
=== Existenz und Eindeutigkeit des Winkelantragens === | === Existenz und Eindeutigkeit des Winkelantragens === | ||
==== Axiom IV.2: (Winkelkonstruktionsaxiom) ==== | ==== Axiom IV.2: (Winkelkonstruktionsaxiom) ==== | ||
| − | :: Es sei <math>\ g \equiv SA</math> eine Gerade in der Ebene <math>\ \varepsilon</math>. Zu jeder reellen Zahl <math>\ \omega</math> mit <math>\ 0 < \omega < 180</math> gibt es in jeder der beiden durch <math>\ g</math> bestimmten Halbebenen der Ebene <math>\ \varepsilon</math> genau einen Strahl <math>\ SB^+</math> mit <math>\ \left| \omega \right| = \left| \angle ASB \right|</math> | + | :: Es sei <math>\ g \equiv SA</math> eine Gerade in der Ebene <math>\ \varepsilon</math>. Zu jeder reellen Zahl <math>\ \omega</math> mit <math>\ 0 < \omega < 180</math> gibt es in jeder der beiden durch <math>\ g</math> bestimmten Halbebenen der Ebene <math>\ \varepsilon</math> genau einen Strahl <math>\ SB^+</math> mit <math>\ \left| \omega \right| = \left| \angle ASB \right|</math>. |
| Zeile 33: | Zeile 39: | ||
::Wenn der Punkt <math>P</math> im Inneren des Winkels <math>\angle ASB</math> und nicht auf einem der Schenkel des Winkels <math> \angle ASB</math> liegt, dann ist die Größe der beiden Teilwinkel <math>\angle ASP</math> und <math>\angle PSB</math> jeweils kleiner als die Größe des Winkels <math>\angle ASB</math>. | ::Wenn der Punkt <math>P</math> im Inneren des Winkels <math>\angle ASB</math> und nicht auf einem der Schenkel des Winkels <math> \angle ASB</math> liegt, dann ist die Größe der beiden Teilwinkel <math>\angle ASP</math> und <math>\angle PSB</math> jeweils kleiner als die Größe des Winkels <math>\angle ASB</math>. | ||
| − | ==== Beweis von Satz V.2 ==== | + | ==== Beweis von Satz V.2 ====<br /> |
| + | |||
| + | '''Lösung von Nummero6/Tchu Tcha Tcha:'''<br /> | ||
| + | |||
| + | '''Vor:''' <br /> | ||
| + | <math>\angle ASB</math>, P liegt im I von <math>\angle ASB</math>, P liegt nicht auf einem der Schenkel von <math>\angle ASB</math><br /> | ||
| + | '''Beh:'''<br /> | ||
| + | <math>\angle ASP</math><math>\le</math><math>\angle ASB</math> oder <math>\angle PSB</math><math>\le</math><math>\angle ASB</math> | ||
| + | <br /> | ||
| + | '''Ann:'''<br /> | ||
| + | oBdA: <math>\angle ASP</math><math>\ge</math> <math>\angle ASB</math> | ||
| + | <br /> | ||
| + | |||
| + | {| class="wikitable" | ||
| + | ! Nr. !! Beweisschritt!!Begründung | ||
| + | |- | ||
| + | |1)|| <math>\angle ASB</math> || Vor | ||
| + | |- | ||
| + | |2) || Es gibt einen Winkel <math>\angle ASP</math>und einen Winkel <math>\angle PSB</math> || laut Voraussetzung (oder muss man zuerst das Winkelkonstruktionsaxiom IV.2 anwenden??) | ||
| + | |- | ||
| + | |3)|| <math>\left| \angle ASP \right| + \left| \angle PSB \right| = \left| \angle ASB \right|</math> || Axiom IV.3 (Winkeladditionsaxiom), (1), (2) | ||
| + | |- | ||
| + | |4)|| Widerspruch zur Annahme || (3) | ||
| + | |- | ||
| + | |5)|| Behauptung stimmt || (4) | ||
| + | |}qed<br />--[[Benutzer:Nummero6|Tchu Tcha Tcha]] 17:01, 10. Jun. 2012 (CEST) | ||
== Rechte Winkel == | == Rechte Winkel == | ||
| Zeile 54: | Zeile 85: | ||
Nach Definition V.6 ist ein rechter Winkel ein solcher, der das selbe Maß wie einer seiner Nebenwinkel hat. | Nach Definition V.6 ist ein rechter Winkel ein solcher, der das selbe Maß wie einer seiner Nebenwinkel hat. | ||
| − | Das Supplementaxiom (Axiom IV.4) besagt, dass die Summe der Größen zweier Nebenwinkel in jedem Fall 180 beträgt. | + | Das Supplementaxiom (Axiom IV.4) besagt, dass die Summe der Größen zweier Nebenwinkel in jedem Fall 180 beträgt.<br /> |
| + | |||
| + | ----Einschub: Das Supplementaxiom besagt doch nur, dass Nebenwinkel supplementär sind..!? Nach der Def. supplementär wissen wir erst, dass" zwei Winkel genau dann supplementär heißen, wenn die Summe ihrer Größen 180 beträgt."...--[[Benutzer:Nummero6|Tchu Tcha Tcha]] 11:45, 1. Jul. 2012 (CEST)<br /> | ||
| + | ---- | ||
Wenn es denn einen rechten Winkel gäbe, so müsste dessen Maß die Hälfte von 180 sein. | Wenn es denn einen rechten Winkel gäbe, so müsste dessen Maß die Hälfte von 180 sein. | ||
| Zeile 79: | Zeile 113: | ||
Bemerkung: Testen Sie ob die Definition korrekt ist: Warum muss nicht gefordert werden, dass die beiden Geraden komplanar sind? | Bemerkung: Testen Sie ob die Definition korrekt ist: Warum muss nicht gefordert werden, dass die beiden Geraden komplanar sind? | ||
| + | |||
| + | =====Frage zur Def. V.8===== | ||
| + | Warum rede ich im Plural wenn es um die Winkel geht? Es reicht doch einer. " ....und bei diesem Schnitt ein rechter Winkel entsteht." oder? <br /> | ||
| + | --[[Benutzer:Kopernikus|Kopernikus]] 20:40, 26. Jun. 2012 (CEST) | ||
| + | |||
| + | =====Antwort M.G.===== | ||
| + | Testen Sie Ihr Verständnis für den bestimmten und den unbestimmten Artikel. | ||
| + | |||
| + | Stellen wir uns vor es gäbe einen und nur einen rechten Winkel, der beim Schnitt zweier zueinander senkrechter Geraden entsteht. Wäre es dann falsch, in der Definition zu fordern, es entstehen rechte Winkel? Sicherlich nicht. Wir könnten genauso fordern, dass rechte Winkel entstehen. Rechte Winkel zu fordern schließt ein, dass eventuell genau ein rechter Winkel existiert. Vielleicht das Ganze noch mal anders: Zwei Geraden <math>g</math> und <math>h</math> stehen senkrecht zueinander, wenn bei ihrem Schnitt ein rechter Winkel entsteht. Diese Definition ist dasselbe wie: Zwei Geraden <math>g</math> und <math>h</math> stehen senkrecht zueinander, wenn bei ihrem Schnitt rechte Winkel entstehen. Wenn mehrere entstehen, entsteht wenigstens einer. Es wäre was anderes, wenn wir fordern würden, dass genau ein rechter Winkel entsteht. Jetzt gäbe es keine zueinander senkrechten Geraden --[[Benutzer:*m.g.*|*m.g.*]] 22:22, 26. Jun. 2012 (CEST) | ||
| + | <br /> | ||
| + | |||
| + | Ja, also ist die Definition von Kopernikus 20:40, 26. Jun. 2012 (CEST) mit ".. und bei diesem Schnitt ein rechter Winkel entsteht." auch korrekt. | ||
| + | Seine Aussage ist doch, dass ein rechter Winkel entsteht.. Es ist aber nicht ausgeschlossen, dass es auch 2, 3 oder 4 sein können. | ||
| + | Das ist doch dieselbe Geschichte, wie mit der Aussage, dass ich "ein Bier" getrunken habe.. | ||
| + | Könnten ja auch mehr gewesen sein.. Ich werde mir morgen, bei einem deutschen Sieg, auch ein Bier gönnen.. :-)<br /> | ||
| + | Es wäre nur nicht korrekt, wenn man schreiben würde, dass bei dem Schnitt "genau ein rechter Winkel" entsteht. Dann gäbe es keinen "Spielraum".<br />--[[Benutzer:Nummero6|Tchu Tcha Tcha]] 17:08, 27. Jun. 2012 (CEST) | ||
===== Definition V.9: (senkrecht für Strecken und Geraden) ===== | ===== Definition V.9: (senkrecht für Strecken und Geraden) ===== | ||
:: Eine Gerade <math>g</math> und eine Strecke <math>\overline{AB}</math> stehen senkrecht zueinander, wenn ... . | :: Eine Gerade <math>g</math> und eine Strecke <math>\overline{AB}</math> stehen senkrecht zueinander, wenn ... . | ||
| + | |||
| + | '' : Eine Gerade <math>g</math> und eine Strecke <math>\overline{AB}</math> stehen senkrecht zueinander, wenn die Gerade <math>g</math> senkrecht auf der Strecke <math>\overline{AB}</math> steht. ''--[[Benutzer:Kopernikus|Kopernikus]] 20:34, 26. Jun. 2012 (CEST) | ||
| + | |||
| + | Ich meine es müsste heißen "...wenn sich die Geraden AB und g schneiden und dabei rechte Winkel entstehen." Eine Strecke kann meines Wissens nach nicht senkrecht auf einer Geraden stehen, sondern nur die Gerade, die durch die beiden Punkte der Strecke eindeutig bestimmt ist.--[[Benutzer:*osterhase*|*osterhase*]] 10:26, 1. Jul. 2012 (CEST)<br /> | ||
| + | |||
| + | ''' @ osterhase ''' | ||
| + | Glaub ich nicht. <br /> | ||
| + | 1. Senkrecht ist bereits Def.<br /> | ||
| + | 2. Schneiden müssen sie sich nicht wegen Def. V.8<br /> | ||
| + | 3. Es geht hier um eine Strecke und um eine Gerade. (Das war ja gegeben) | ||
| + | --[[Benutzer:Kopernikus|Kopernikus]] 18:15, 5. Jul. 2012 (CEST) | ||
| + | |||
===== Definition V.10: (senkrecht für Strecken)===== | ===== Definition V.10: (senkrecht für Strecken)===== | ||
:: Zwei Strecken <math>\overline{AB}</math> und <math>\overline{PQ}</math> stehen senkrecht zueinander, wenn ... . | :: Zwei Strecken <math>\overline{AB}</math> und <math>\overline{PQ}</math> stehen senkrecht zueinander, wenn ... . | ||
| + | '' : Eine Stecke <math>\overline{AB}</math> und eine Strecke <math>\overline{PQ}</math> stehen senkrecht zueinander, wenn sich die Strecke <math>\overline{AB}</math> und die Stecke <math>\overline{PQ}</math> senkrecht aufeinander stehen. ''<br /> | ||
| + | --[[Benutzer:Kopernikus|Kopernikus]] 20:56, 26. Jun. 2012 (CEST) | ||
| + | |||
| + | Same procedure: Die Gerade AB und die Gerade PQ stehen senkrecht aufeinander, wenn...--[[Benutzer:*osterhase*|*osterhase*]] 10:27, 1. Jul. 2012 (CEST) | ||
| + | <br /> | ||
| + | ''' @ osterhase ''' Genau das Gleiche.... | ||
| + | Es wir in der Def. gefordert das es sich um zwei Stecken handelt und nicht um Geraden | ||
| + | --[[Benutzer:Kopernikus|Kopernikus]] 18:18, 5. Jul. 2012 (CEST) | ||
| + | |||
===== Definition V.11: (senkrecht für Ebenen und Geraden)===== | ===== Definition V.11: (senkrecht für Ebenen und Geraden)===== | ||
::Eine Gerade <math>g</math> steht senkrecht auf einer Ebene <math>\varepsilon</math> wenn, ... . | ::Eine Gerade <math>g</math> steht senkrecht auf einer Ebene <math>\varepsilon</math> wenn, ... . | ||
| + | Eine Gerade <math>g</math> steht senkrecht auf einer Ebene <math>\varepsilon</math>, wenn die Gerade <math>g</math> die Ebene <math>\varepsilon</math> in geanu einem Punkt <math>P</math> schneidet und zu zwei nichtidentischen Geraden die durch <math>P</math> gehen und in der Ebene <math>\varepsilon</math> liegen orthogonal ist. ''<br /> | ||
| + | --[[Benutzer:Kopernikus|Kopernikus]] 20:56, 26. Jun. 2012 (CEST)+--[[Benutzer:Snooth|Snooth]] 18:07, 28. Jun. 2012 (CEST) | ||
| + | |||
===== Definition V.12: (senkrecht für Ebenen)===== | ===== Definition V.12: (senkrecht für Ebenen)===== | ||
| − | ::Eine Ebene <math>\varepsilon</math> steht senkrecht auf einer Ebene <math>\alpha</math>, wenn ... . | + | ::Eine Ebene <math>\varepsilon</math> steht senkrecht auf einer Ebene <math>\alpha</math>, wenn ... |
| + | ...die Schnittmenge der beiden Ebenen eine Gerade (g) ist, <math>S</math> <math>\in</math> Gerade (g), <math>P_1</math> <math>\in</math> <math>\varepsilon</math>, | ||
| + | <math>P_2</math> <math>\in</math> <math>\alpha</math> und <math>\left| \angle P_1SP_2 \right| = 90</math> gilt.<br />--[[Benutzer:Nummero6|Tchu Tcha Tcha]] 22:03, 26. Jun. 2012 (CEST) | ||
| + | <br /> | ||
| + | <br /> | ||
| + | ... eine Gerade <math>g</math> in <math>\varepsilon</math> liegt, eine Gerade <math>s</math> in <math>\alpha</math> liegt und <math> g\perp s</math> gilt. | ||
| + | <br /> | ||
| + | :Ist die Definition so sinnvoll? | ||
| + | :Mein Gedanke war: Wenn zwei Geraden senkrecht zueinander verlaufen, dann müssen auch die Ebenen in welchen sie liegen senkrecht zueinander sein. | ||
| + | --[[Benutzer:Snooth|Snooth]] 19:26, 28. Jun. 2012 (CEST) | ||
==== Eigenschaften der Relation senkrecht ==== | ==== Eigenschaften der Relation senkrecht ==== | ||
| Zeile 106: | Zeile 189: | ||
===== Beweis von Satz V.5 ===== | ===== Beweis von Satz V.5 ===== | ||
Aufgabe_Tutorium | Aufgabe_Tutorium | ||
| − | [[ | + | |
| + | ==Einige Lemmata zu Winkeln== | ||
| + | Die Lemmata noch mal in einer eigenen Datei: | ||
| + | [[Lemmata zu Winkeln]] | ||
| + | ===Vorbemerkungen=== | ||
| + | Unter einem Lemma versteht der Mathematiker einen Hilfssatz. Wir geben hier die folgenden Hilfssätze an, die wir im weiteren verwenden werden, ohne sie hier bewiesen zu haben. Die Beweise dieser Lemmata sind nicht wirklich schwer aber unerquicklich. | ||
| + | |||
| + | Wer sich für die Beweise interessiert findet sie hier: | ||
| + | |||
| + | [http://www.ph-heidelberg.de/wp/gieding/lehre/Geometrieeinfuehrung/pdf_07_08/V08.pdf] | ||
| + | |||
| + | ===Lemma W/1=== | ||
| + | ::Gegeben seien drei nicht kollineare Punkte <math>A, B, S</math>. Wenn <math>P</math> ein Punkt der offenen Strecke <math>\overline{AB}</math> ist, dann liegt der Strahl <math>SP^+</math> vollständig im Inneren von <math>\angle ASB</math>. | ||
| + | |||
| + | [[Datei:Lemma01.jpg]] | ||
| + | ===Lemma W/2=== | ||
| + | ::Liegt ein Punkt <math>P</math> im Inneren eines Winkels mit dem Scheitel <math>S</math>, dann liegt der gesamte Strahl <math>SP^+</math> im Inneren dieses Winkels. | ||
| + | ===Lemma W/3=== | ||
| + | ::Es seien <math>A,B,S</math> drei nichtkollineare Punkte. WEenn der Punkt <math>P</math> im Inneren des Winkels <math>\angle ASB</math> und nicht auf den Schenkeln dieses Winkels liegt, dann schneidet der Strahl <math>SP^+</math> die offene Strecke <math>\overline{AB}</math>. | ||
| + | |||
| + | <!--- Was hier drunter steht muss stehen bleiben ---> | ||
| + | |} | ||
| + | </div> | ||
| + | |||
| + | [[Kategorie:Einführung_S]] | ||
Aktuelle Version vom 5. Juli 2012, 17:20 Uhr
|
Das WinkelmaßWas bedeutet es, die Größe eines Winkels zu messen?
Das WinkelmaßaxiomAxiom IV.1 (Winkelmaßaxiom)
Definition V.5: (Größe eines Winkels)
WinkelkonstruktionExistenz und Eindeutigkeit des WinkelantragensAxiom IV.2: (Winkelkonstruktionsaxiom)
WinkeladditionAxiom IV.3: (Winkeladditionsaxiom)
Satz V.2
==== Beweis von Satz V.2 ==== Lösung von Nummero6/Tchu Tcha Tcha: Vor:
oBdA:
--Tchu Tcha Tcha 17:01, 10. Jun. 2012 (CEST) Rechte WinkelDefinition V.6 : (Rechter Winkel)
Definition V.7 : (Supplementärwinkel)
Axiom IV.4: (Supplementaxiom)
Satz V.3 : (Existenz von rechten Winkeln)
Beweis von Satz V.3 :Wir haben zu zeigen, dass wenigstens ein rechter Winkel existiert. Nach Definition V.6 ist ein rechter Winkel ein solcher, der das selbe Maß wie einer seiner Nebenwinkel hat. Das Supplementaxiom (Axiom IV.4) besagt, dass die Summe der Größen zweier Nebenwinkel in jedem Fall 180 beträgt. Einschub: Das Supplementaxiom besagt doch nur, dass Nebenwinkel supplementär sind..!? Nach der Def. supplementär wissen wir erst, dass" zwei Winkel genau dann supplementär heißen, wenn die Summe ihrer Größen 180 beträgt."...--Tchu Tcha Tcha 11:45, 1. Jul. 2012 (CEST) Wenn es denn einen rechten Winkel gäbe, so müsste dessen Maß die Hälfte von 180 sein.
In der Tat gibt es einen derartigen Winkel: Das Axiom IV.2 (Winkelkonstruktionsaxiom) besagt, dass es in jeder der beiden Halbebenen einer Ebene bezüglich etwa der Geraden Satz V.4 :
Beweis von Satz V.4 :
Die Relation Senkrecht auf verschiedenen PunktmengenDefinition V.8 : (Relation senkrecht auf der Menge der Geraden)
Bemerkung: Testen Sie ob die Definition korrekt ist: Warum muss nicht gefordert werden, dass die beiden Geraden komplanar sind? Frage zur Def. V.8Warum rede ich im Plural wenn es um die Winkel geht? Es reicht doch einer. " ....und bei diesem Schnitt ein rechter Winkel entsteht." oder? Antwort M.G.Testen Sie Ihr Verständnis für den bestimmten und den unbestimmten Artikel. Stellen wir uns vor es gäbe einen und nur einen rechten Winkel, der beim Schnitt zweier zueinander senkrechter Geraden entsteht. Wäre es dann falsch, in der Definition zu fordern, es entstehen rechte Winkel? Sicherlich nicht. Wir könnten genauso fordern, dass rechte Winkel entstehen. Rechte Winkel zu fordern schließt ein, dass eventuell genau ein rechter Winkel existiert. Vielleicht das Ganze noch mal anders: Zwei Geraden Ja, also ist die Definition von Kopernikus 20:40, 26. Jun. 2012 (CEST) mit ".. und bei diesem Schnitt ein rechter Winkel entsteht." auch korrekt.
Seine Aussage ist doch, dass ein rechter Winkel entsteht.. Es ist aber nicht ausgeschlossen, dass es auch 2, 3 oder 4 sein können.
Das ist doch dieselbe Geschichte, wie mit der Aussage, dass ich "ein Bier" getrunken habe..
Könnten ja auch mehr gewesen sein.. Ich werde mir morgen, bei einem deutschen Sieg, auch ein Bier gönnen.. :-) Definition V.9: (senkrecht für Strecken und Geraden)
: Eine Gerade Ich meine es müsste heißen "...wenn sich die Geraden AB und g schneiden und dabei rechte Winkel entstehen." Eine Strecke kann meines Wissens nach nicht senkrecht auf einer Geraden stehen, sondern nur die Gerade, die durch die beiden Punkte der Strecke eindeutig bestimmt ist.--*osterhase* 10:26, 1. Jul. 2012 (CEST) @ osterhase
Glaub ich nicht. Definition V.10: (senkrecht für Strecken)
: Eine Stecke Same procedure: Die Gerade AB und die Gerade PQ stehen senkrecht aufeinander, wenn...--*osterhase* 10:27, 1. Jul. 2012 (CEST)
Definition V.11: (senkrecht für Ebenen und Geraden)
Eine Gerade Definition V.12: (senkrecht für Ebenen)
...die Schnittmenge der beiden Ebenen eine Gerade (g) ist,
--Snooth 19:26, 28. Jun. 2012 (CEST) Eigenschaften der Relation senkrecht
Satz V.5: (Existenz und Eindeutigkeit der Senkrechten zu einer Geraden auf einem Punkt dieser Geraden)
Beweis von Satz V.5Aufgabe_Tutorium Einige Lemmata zu WinkelnDie Lemmata noch mal in einer eigenen Datei: Lemmata zu Winkeln VorbemerkungenUnter einem Lemma versteht der Mathematiker einen Hilfssatz. Wir geben hier die folgenden Hilfssätze an, die wir im weiteren verwenden werden, ohne sie hier bewiesen zu haben. Die Beweise dieser Lemmata sind nicht wirklich schwer aber unerquicklich. Wer sich für die Beweise interessiert findet sie hier: Lemma W/1
Lemma W/2
Lemma W/3
|
 gibt es genau eine reelle Zahl
gibt es genau eine reelle Zahl 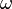 zwischen 0 und 180.
zwischen 0 und 180.
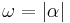 .
.
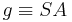 eine Gerade in der Ebene
eine Gerade in der Ebene  . Zu jeder reellen Zahl
. Zu jeder reellen Zahl 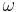 mit
mit 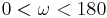 gibt es in jeder der beiden durch
gibt es in jeder der beiden durch  bestimmten Halbebenen der Ebene
bestimmten Halbebenen der Ebene 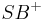 mit
mit 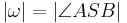 .
.
 zum Inneren des Winkels
zum Inneren des Winkels  gehört , dann gilt
gehört , dann gilt 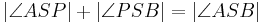 .
.
 im Inneren des Winkels
im Inneren des Winkels  und nicht auf einem der Schenkel des Winkels
und nicht auf einem der Schenkel des Winkels 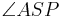 und
und 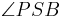 jeweils kleiner als die Größe des Winkels
jeweils kleiner als die Größe des Winkels 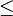
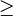
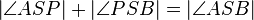
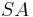 zu jeder beliebigen Zahl zwischen 0 und 180 genau einen Winkel
zu jeder beliebigen Zahl zwischen 0 und 180 genau einen Winkel 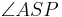 gibt, dessen Größe gerade die Zahl zwischen 0 und 180 ist. Die Zahl 90 ist größer als 0 und kleiner als 180 und demzufolge als Winkelmaß zulässig.
gibt, dessen Größe gerade die Zahl zwischen 0 und 180 ist. Die Zahl 90 ist größer als 0 und kleiner als 180 und demzufolge als Winkelmaß zulässig.
 und
und  zwei Geraden. Wenn sich
zwei Geraden. Wenn sich 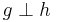 (in der Formelbeschreibungssprache Tex: \perp , läßt sich gut merken, von perpendicular)
(in der Formelbeschreibungssprache Tex: \perp , läßt sich gut merken, von perpendicular)
 stehen senkrecht zueinander, wenn ... .
stehen senkrecht zueinander, wenn ... .
 stehen senkrecht zueinander, wenn ... .
stehen senkrecht zueinander, wenn ... .
 wenn, ... .
wenn, ... .

 Gerade (g),
Gerade (g), 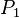
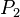
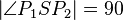 gilt.
gilt. in
in 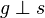 gilt.
gilt.
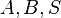 . Wenn
. Wenn 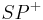 vollständig im Inneren von
vollständig im Inneren von