Lösung von Aufgabe 9.4P (SoSe 12): Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: „''m'' sei Mittelsenkrechte der Strecke <math>\overline{AB}</math>. Beweisen Sie durch Kontraposition und mit Hilfe abbildungsgeometrischer Betrachtungen: <math>\l…“) |
|||
| (6 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
''m'' sei Mittelsenkrechte der Strecke <math>\overline{AB}</math>. Beweisen Sie durch Kontraposition und mit Hilfe abbildungsgeometrischer Betrachtungen: <math>\left| AP \right| =\left| BP \right|\Rightarrow P\in m</math> | ''m'' sei Mittelsenkrechte der Strecke <math>\overline{AB}</math>. Beweisen Sie durch Kontraposition und mit Hilfe abbildungsgeometrischer Betrachtungen: <math>\left| AP \right| =\left| BP \right|\Rightarrow P\in m</math> | ||
| − | <br /> | + | <br /><br /> |
| + | Hilfreiche Sätze für den Beweis könnten sein: <math>| AP=\left| BP \|\Rightarrow P\in m </math>, Dreiecksungleichung<br /> Und eine Skizze hilft auch schon!--[[Benutzer:Tutorin Anne|Tutorin Anne]] 15:29, 26. Jun. 2012 (CEST)<br /> | ||
[[Kategorie:Einführung_P]] | [[Kategorie:Einführung_P]] | ||
| + | <br /> | ||
| + | Voraussetzung: Strecke AP = Strecke BP | ||
| + | |||
| + | Behauptung: P ist Element von m | ||
| + | |||
| + | Kontraposition: P nicht Element m | ||
| + | |||
| + | Fall 1: | ||
| + | |||
| + | P liegt in der selben HE wie B | ||
| + | |||
| + | 1.Strecke BP geschnitten mit m= leere Menge (Def. HE, Ann.) | ||
| + | |||
| + | 2. Strecke AP geschnitten mit m= S (1. Def. HE)<br /> | ||
| + | Woher weißt du, dass A in der anderen HE liegt?--[[Benutzer:Tutorin Anne|Tutorin Anne]] 15:45, 2. Jul. 2012 (CEST) | ||
| + | |||
| + | 3. S ist Element von der Strecke AP (1.2) | ||
| + | |||
| + | 4. ZW(A,S,P) (3.) | ||
| + | |||
| + | 5. Strecke AS+ Strecke SP= Strecke AP (Def. ZW) | ||
| + | |||
| + | 6. Strecke AP ist größer als Strecke BP (Widerspruch zur Vor.) | ||
| + | Wie kommst du auf Schritt 6? Was hat dieser mit den vorrigen Schritten zu tun?--[[Benutzer:Tutorin Anne|Tutorin Anne]] 15:45, 2. Jul. 2012 (CEST) | ||
| + | |||
| + | Fall 2: | ||
| + | |||
| + | P liegt in der selben HE wie A | ||
| + | |||
| + | analog--[[Benutzer:Geogeogeo|Geogeogeo]] 12:45, 30. Jun. 2012 (CEST)<br /> | ||
| + | |||
| + | Danke für dein Beitrag Geogeogeo - die Beweisidee stimmt und die Schritte hast du meist begründet. An zwei Stellen konnte ich nicht folgen oder habe die Begründung nicht verstenden. Wie kann man das noch verbessern oder verändern? - Das ist eine Frage an alle!--[[Benutzer:Tutorin Anne|Tutorin Anne]] 15:45, 2. Jul. 2012 (CEST) | ||
Aktuelle Version vom 2. Juli 2012, 14:45 Uhr
m sei Mittelsenkrechte der Strecke 
. Beweisen Sie durch Kontraposition und mit Hilfe abbildungsgeometrischer Betrachtungen: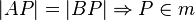 
Hilfreiche Sätze für den Beweis könnten sein: Fehler beim Parsen(Syntaxfehler): | AP=\left| BP \|\Rightarrow P\in m
, Dreiecksungleichung
Und eine Skizze hilft auch schon!--Tutorin Anne 15:29, 26. Jun. 2012 (CEST)
Voraussetzung: Strecke AP = Strecke BP
Behauptung: P ist Element von m
Kontraposition: P nicht Element m
Fall 1:
P liegt in der selben HE wie B
1.Strecke BP geschnitten mit m= leere Menge (Def. HE, Ann.)
2. Strecke AP geschnitten mit m= S (1. Def. HE)
Woher weißt du, dass A in der anderen HE liegt?--Tutorin Anne 15:45, 2. Jul. 2012 (CEST)
3. S ist Element von der Strecke AP (1.2)
4. ZW(A,S,P) (3.)
5. Strecke AS+ Strecke SP= Strecke AP (Def. ZW)
6. Strecke AP ist größer als Strecke BP (Widerspruch zur Vor.)
Wie kommst du auf Schritt 6? Was hat dieser mit den vorrigen Schritten zu tun?--Tutorin Anne 15:45, 2. Jul. 2012 (CEST)
Fall 2:
P liegt in der selben HE wie A
analog--Geogeogeo 12:45, 30. Jun. 2012 (CEST)
Danke für dein Beitrag Geogeogeo - die Beweisidee stimmt und die Schritte hast du meist begründet. An zwei Stellen konnte ich nicht folgen oder habe die Begründung nicht verstenden. Wie kann man das noch verbessern oder verändern? - Das ist eine Frage an alle!--Tutorin Anne 15:45, 2. Jul. 2012 (CEST)
