Lösung von Aufgabe 11.4P (SoSe 12): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(Die Seite wurde neu angelegt: „Zeigen Sie, dass die Verkettung einer Drehung <math>D_{\left( S,\alpha \right) } </math> mit einer Verschiebung wieder eine Drehung <math>D_{\left( P,\alpha \righ…“) |
|||
| (2 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
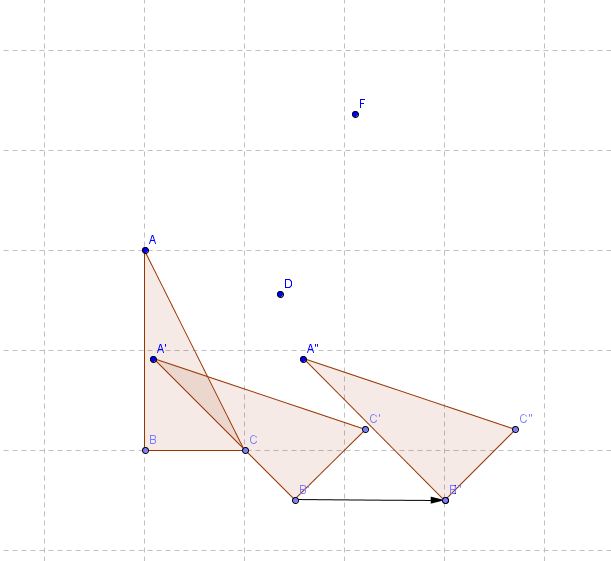
Zeigen Sie, dass die Verkettung einer Drehung <math>D_{\left( S,\alpha \right) } </math> mit einer Verschiebung wieder eine Drehung <math>D_{\left( P,\alpha \right) } </math> ergibt. Wo liegt das neue Drehzentrum ''P''? | Zeigen Sie, dass die Verkettung einer Drehung <math>D_{\left( S,\alpha \right) } </math> mit einer Verschiebung wieder eine Drehung <math>D_{\left( P,\alpha \right) } </math> ergibt. Wo liegt das neue Drehzentrum ''P''? | ||
| − | <br /> | + | <br /><br />[[Datei:11.4.JPG]]<br />--[[Benutzer:Studentin|Studentin]] 22:53, 1. Jul. 2012 (CEST)<br /> |
| + | hier noch die konstruktion von punkt p nachgeliefert :<br /> | ||
| + | <ggb_applet width="1281" height="493" version="4.0" ggbBase64="UEsDBBQACAgIACEI5EAAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAgIACEI5EAAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s5VvbbuM2Gr6ePgWhi71YjGWeJFmzzhTjFMUOkHaCZlos9mZBS7SjRpa8kuzERR9qn2GfbH+SkizZimM7h3GyRlMd+JM/+X3/ibRn+P3dLEZLmeVRmpxZxMYWkkmQhlEyPbMWxaQ3sL7/+N1wKtOpHGcCTdJsJooziyvJKDyzBhMvwM540BOYhz3uD9yeP/Fpb0z8MfFYICj2LITu8uhDkv4sZjKfi0BeBddyJi7SQBRa8XVRzD/0+7e3t3alyk6zaX86Hdt3eWghmGaSn1nlzQcYrtXplmlxijHp/+OnCzN8L0ryQiSBtJBawiL6+N274W2UhOktuo3C4hoWTH2Y3bWMptewKJfBovpKag6IzGVQREuZQ9/Go150MZtbWkwkqv2duUNxvR4LhdEyCmV2ZmGbeJj5jBKHEOL5LncslGaRTIpSmJRK+9Vww2Ukb8246k6r5BYq0jQeCzUk+vNPRDHF6L26EHOhcHFd04TNO8zMhZoLNxfHyHDTnRtRbmS4keHMQssoj8axPLMmIs4BwyiZZMBf/ZwXq1jq+ZQv1ssn72FNefQHCDMMmBrQ4T3G79WfC38cl2A3FkkaWotscaDSSiWhA7K/TvqolbJKKaUdOqlzzzrdHUrNwvdaqNPAFlTp//Tflka2a5mbGs3z4xS6/EWWOOxXvjIs3QPl10q2NJ9CznLlMMxHjq/sniAHnMP1wMwdRHy4eBSBOyDiIO7AIxkgV109xDxo4IihAVJyhCHtHc4A/sc9PZiLHBhMvfXAKREBRRw5DBHtVByBKyHtmOCklIGE4yAHOin1hKohmIu4C09sgDjMUfmkR0CQQUd4BvUUMYKY6kw8RF3kqvEIV77uDtTUYUiKXIxcogYEtwaXNu4M8gPE1GrcEq4omS+KFkTBLKxui3RecwHSEJDWcc8EqFZYfDeMxVjGkCquFJMILUWsPEIrmqRJgWqHNO+mmZhfR0F+JYsCeuXod7EUF6KQdz+CdF7p1rJBmuSXWVqcp/FiluQIBWmM6zmnMWnc03rW8MAaDbzZ4DQa3Ma916k3hRa0yCXoT7O8Ehdh+FlJrEMDIPkliVejTIqbeRq1lzHs66wzlIsgjsJIJL+BsSotChe0TkIqXlVJiPu0mkmahVerHEwY3f1TZilgy12bNT8WWpkW6vs2aXzA3fNAxDow2bTxIb7q1N1GCTeq5bKmSNzJ9WqnmXLtxsPnfJTG61cagHMxLxaZLiBAVaZW9SmZxlIbiXZtyM7BzTi9uzLWwcxYX1dzeMJmBuOpBh5BcKAOJMxpeR2bq5ZRU6ulsJbBWgJX5haFdTsBWJWEvo7NVUuB/ZqplUsl1TIJrtREuQ5p2CodpwpXyvpVrl8kUXFRPRRRcLNequrw82I2lrUNtcckTzXmsL9hZMMbmSUyLm0ayFyki9y4aMPcQxlEM3g0DSUkQtH1K0zAvA3lNJPVxGNdnBnAdCtuWuvWaz3Uj1k6+5wsv4ItbExg2K9mOcyDLJorm0NjyAM3cm1VYZQLSCNhs59yQlh6oNIFwFMoaMA9F8V1munyC6IKXJXvxXIGtRYqtHlpC61h/qSrOIUnSse/Q2Crc59pXxMGzZ2mpo1SxPNroSq9ctGxWMmsBYMe76c03AQHsNcrACefG27nUhqzMPOFmzkMp72pFaUA7RzdnVk9ZmNItSvIjjZY9h+miDdFrFqr8rFWYDZvN4gC6zEwPQDY6A0ARivAmK3qsGdG7Pz1I8Zs19WAcdt9GhML0tlMJCFKdDV4mcaraZpY6/pEYOWbSBBlcUhQBaPBaFFU7RDlYkgjxIgFRkzABQqAsVFYqulgyCisOKiHaueDAmqVG9iR5XqTUJTpSd/8PQpDqevU/m56G4A2+SUO0ww7pExYa4LJIQTfb4W5nKqneiLBA3Z4+EQPtMS1PdUOqI8bjDlh4vjrz2AzNe9Phfx3YrrkJl9Gs3kcBVFR20+sLP1zUkD2lDp9bCfFGynnqhr5knzNRJKrMw8j00i2e8IuTgf2HrG5W2YKT+Peo9j2fczfDNrjE0Ib284ANz9EY99zS/AZJG7Pfb2W3k5zV0eluaq0N4mOYPptE532C53nON+Z55yj8twvaQFVaXea8/Ff//sfk8OutlLdp7+IeZr/7aGk1qpsyy7ftPhYI8ttn/nNj2OcgdvsGQqKTqBHewA9Ohzo0WkB7dqQPDW07OWgPd8D2vPDoT0/LWgd26GtgG5smNq89RbvDh1PWiKXAJlCuX6gLbQ7i+Zmx6DZUdQPqozej7PuYrpB3lstqfeyz2ee7kaFh0ubxC2jJMYkme2RpgmzV1t8bJXZJ0dFVUuUVbcq+CAJvuJ6b6vWPjXI3QrxzcrbWH+PQQDfPvR9Nfi3c+MP27i3T5Bf+FxJ8XZ4wU2wzWl5Fuc9R978DZBJs81ypZn9ftjKkYvd+W5phqxwXhznAE+482lW2QO/o8omNmsX375Geq3oCGdoHPeX7hCIrJB5JJIyfxfwfKnYQvJuvlH/3UeXdoq4Y5PUZGxx3/7o6F3SadWZvj0wx2M9CgnjGZziPpRHu1EeHYvy6BRRJsQeeBtOYdL1i2J+vhvz82MxPz9JzJ873O/cJnVsljq2THttnDq2Tx2bqI6t1OM3VP8326pTKy+bmyu2nU2JA/Fk8HaO0sWJstDcVznbNLhQAzn87dAwPk0a7t1rVZst17Ndzl/TbredSa5KHjoPOneninB3eN9kODyOVdz6TZTi9vH5GW+WRKYmArLdcgvNwele0xZ6H1JHXSXBJqnyMFLlU5D6ZOfWxBRdhNk+abI7KFlltsPpa4qZ+9BafrG2tTds0To5jNbJcbQq71wH4CeidaB/vaRopds7GUUrpyABm5nXSusFTHkU5V0nOOEWkbOoKCRoTW4yGVwX8l9kN7MKj5q2js7H75iOCMlfJpNcFrq88UxepXQ/I+iZ2Lzqjt1gBVz5/DNF7KOokw9S9wjinoC2Q7yzwRstv9D29t1MdMTiVRWrVR3r2Jzwxj7jhCicPOx99DHeR4+i8fggu6aRljs8vi+LHaF3VYVm85WP61Dv27FYB+cNCjsins6WXb7YYvrykEOoyxf+UdCayPKreWfPcynYrVCXe+6g/mJUJ1bXt7HD3PJAkFKbucTtPK7a9wdB/ebv1vW/Dyn/tePH/wFQSwcIVNU+RUoJAACKOQAAUEsBAhQAFAAICAgAIQjkQNY3vbkZAAAAFwAAABYAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhX2phdmFzY3JpcHQuanNQSwECFAAUAAgICAAhCORAVNU+RUoJAACKOQAADAAAAAAAAAAAAAAAAABdAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAACAAIAfgAAAOEJAAAAAA==" showResetIcon = "false" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" />--[[Benutzer:Studentin|Studentin]] 01:02, 4. Jul. 2012 (CEST)<br /> | ||
| + | sehr gutes Beispiel!--[[Benutzer:Tutorin Anne|Tutorin Anne]] 20:16, 5. Jul. 2012 (CEST)<br /> | ||
| + | Du hast das jetzt an einem Beispiel gezeigt, dass gibt aber noch keine allgemeine Erklärung oder Begründung, dass aus einer | ||
| + | Verkettung der zwei Bewegungen wirklich immer eine Drehung entsteht. Und wo liegt dann das Drehzentrum in Abhängigkeit der | ||
| + | Spiegelachsen?--[[Benutzer:Tutorin Anne|Tutorin Anne]] 09:08, 10. Jul. 2012 (CEST) | ||
[[Kategorie:Einführung_P]] | [[Kategorie:Einführung_P]] | ||
Aktuelle Version vom 10. Juli 2012, 08:08 Uhr
Zeigen Sie, dass die Verkettung einer Drehung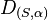 
mit einer Verschiebung wieder eine Drehung 
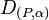ergibt. Wo liegt das neue Drehzentrum P?
--Studentin 22:53, 1. Jul. 2012 (CEST)
hier noch die konstruktion von punkt p nachgeliefert :
sehr gutes Beispiel!--Tutorin Anne 20:16, 5. Jul. 2012 (CEST)
Du hast das jetzt an einem Beispiel gezeigt, dass gibt aber noch keine allgemeine Erklärung oder Begründung, dass aus einer Verkettung der zwei Bewegungen wirklich immer eine Drehung entsteht. Und wo liegt dann das Drehzentrum in Abhängigkeit der Spiegelachsen?--Tutorin Anne 09:08, 10. Jul. 2012 (CEST)
