04.07.2012: Streckung - Drehung: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
HecklF (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „=Original oder Fälschung?= ==Welche der beiden Kurven ist eine Asteroidenkurve?== <ggb_applet width="1000" height="750" version="4.0" ggbBase64="UEsDBBQACAAIAPV…“) |
HecklF (Diskussion | Beiträge) (→Wie gehen wir vor?) |
||
| (2 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 4: | Zeile 4: | ||
<br />--[[Benutzer:HecklF|Flo60]] 14:16, 4. Jul. 2012 (CEST) | <br />--[[Benutzer:HecklF|Flo60]] 14:16, 4. Jul. 2012 (CEST) | ||
| + | ===Begründung=== | ||
| + | <br /> | ||
| + | |||
| + | |||
| + | |||
| + | <br /> | ||
==Berechne Punkt F== | ==Berechne Punkt F== | ||
<br /> | <br /> | ||
| Zeile 11: | Zeile 17: | ||
<br /> | <br /> | ||
| + | |||
| + | =Man schätze die Fläche der Asteroide= | ||
| + | ==Folgende Applikation kann behilflich sein:== | ||
| + | <ggb_applet width="800" height="700" version="4.0" ggbBase64="UEsDBBQACAAIADtz5EAAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiu5QIAUEsHCEXM3l0aAAAAGAAAAFBLAwQUAAgACAA7c+RAAAAAAAAAAAAAAAAADAAAAGdlb2dlYnJhLnhtbO1a627bOBb+3XkKQr+6i9omqYvlwunAyUzaAp0LkO5isT+2oCRa5kQWtSLt2MU81D7DPtkekpJ8S9LGaYokWKAub0fn8HznKjvjH1fzAi15rYQsTzzSxx7iZSozUeYn3kJPe7H345sfxjmXOU9qhqaynjN94gWGUmQnXpZkAfaHo142JUkvCFPci2k67LEkjdI4oQnhQw+hlRKvS/krm3NVsZRfpDM+Zx9kyrQVPNO6ej0YXF1d9VtRfVnngzxP+iuVeQiuWaoTr5m8BnY7D135lpxiTAb/+OWDY98TpdKsTLmHjAoL8eaHF+MrUWbyCl2JTM9AYRqDHjMu8hkoNYoDDw0MVQWIVDzVYskVPLu1tErreeVZMlaa8xduhopOHw9lYikyXp94uO+HHpK14KVuTkkjZdA+P14KfuUYmZmVAVfRUhYJMzzQn38iiilGr8xA3EBhiCJ3hN0e9t1A3RC4IXQ0gXs8cKSBowkcTeB7aCmUSAp+4k1ZoQA0UU5rMFi3VnpdcHufZmOjL3kFOinxGYh9DIg6lGEf41fmE8EnMAeDXSXJllRdL+4otBVJaBR8vUx6L039VmgQxIcyaXiDntEtQp3iX6VouIUtiLL/7OdAon+bmvsS3fp+Ao0JvoOK40EbK+MmPJCaGdrGfTSfKxMw/giFI+P3BIUQHNEQ3DxEZATDkCIIB0RCFISwJDGKzDhE/hAOAuSjGBk64iMbHWEM/wVDyyxCITAzu0MISkRAUIBCHxEbVAGCUEI2MCFIqQ8UYYhCeMiIJ9Sw8CMURLDyYxTAHU1MDgkQ+vAgrEE8RT5BvnmYDBGNUGT4kcDEehSbqwNLiiKMImIYQlhDSLtwBvoY+UabqIFLlNVC70CUzrN2qmXV2QKoISFtEp1LUDt58MW4YAkvoDZcGEsitGSFiQgraCpLjbqAdHt5zaqZSNUF1xqeUugPtmQfmOarc6BWrWxLm8pS/V5LfSaLxbxUCKWywN2dZUG25rS7NSz8rYNg+yDcOoi25sNr5Uo4QQvFQb6sVUvOsuy9odikBkDyt7JYn9acXVZS7KoxHtgyM+aLtBCZYOXfwVmNFIML2lQdEyxt1YnJqL2JrLOLtQIXRqt/8lpCrhpGfcgrhASUxsN4NIJSsnZH/iju0yCIKI5GISHUB4urlJnoIzHtxyM8ijAdjXBIAqjA6+vPGkPxZWcituKd9nktsu35e3Uqi6zDwqp/xiq9qG2/ALmxNjpNyrzg1kVstoVinF4mcnXhfMN3vD6uK1hhJz/JLewIUgMNQce8GRM3WhpzsY4KWxpsKXDrbCLrzsmIWgo7Jm60VOC97mqNoqTVkuBWjFA2oWFvJ2ys65vKviiF/tAutEgvG02Jo/91MU9450C7LMk3Yjke7DnY+JLXJS8afwZDLuRCufDccvWMp2IOS3fQAMKMsf4GF3C7Gc9r3t67sJ2Yg8ue4m1PPdi2rM5rOX9fLj+CJ+xdYDxobzlWaS0q428ogRpwyTc+lQnFoIRk28+ZAATVU1MqAB5toIHQXOiZrG2vBRkFRks5n7MyQ6WtOmeLesnPWK25AqS8TTpkkFhSqV5CcvoLMILUokTZriC5wAwmvvUBBjnFj/Bf//sfp6Rc6JYFc1o1Qk3YF3wObR7S1rdTIz7txLfmZvYixq5IJn9Act2UQ0ewZTEguMHlESuqGTPtZQN+wda83jGHZfeLzHaNtAkADan5EhpQZaNUN/FoJ+9ElnFblp23Ob2OA/hfL/09kJudrwc6OQro5BDonbh7QjiLOi34Hr4v8SuEG2TJAWTpFyCTpUg7JNInhhQULJHzEoyuoVbD2yVu3l3X2MlHn9udFaDTs1tr0mx9biaWEbzN1mKFJi39pKWagHv23MxvmE6CltckbGbuMv8u3f2VS9umZRJTke4bddcEtnp2EE++YIJNNbnJArZgHmsDVkJlsPkV2o/KVZ6Kc1ez3H1hUgE7W+l3+ieoBQqtWgu0IG9hbDU11X+nYXS7e0Xk5hj43cK1GwLJgduf3u72u5ifHoU5oa5BseNjwB0/KO7X5p6JSzunB/hnd0k72f/TzrVp55qsQ7qsQ75l1jl7+lmn963Tzm14/fSM8Op9D8B+fvqAfXO89utasc7lfvN85hLsT65N/tk1yZODdAtvfwW8XBNHnX4ijj6zE3iCu7aafSJfqovuEq1ZOr7HJso7J3US+q6qmvHA7OQuZr/ZNxXPzWrT934ix5Wg2297RyfduBptXA03nkb796lVe/VBzKtCpEJ3TlQYp39fal4rbt+tD78xuOS8Ml/U/FZ+rFmpzK8/jmbrm4ivxDp7ZFi3XRN9hljzR4V07zm7NXukbt17mn795Xe+9NPhlx3nd3nrO38eb31dH4cfqC05hD67Bvq3d4H+7fOAHj9sR9iF077nuy4vcz0ePTDFu7uY4t1RpjC/W+VuSNxw/4z10H58XXt96qA8d1C+dc3yu5vaa+qok7a9njr63DXXs6Naa/r9Wmt88HvagzfWybFV8ba73tvDDuP1SdTE26GePkKgnyPO+SPC+ebvvJ4B0LPHCPQTTR2D7Z/O7Z+nNH9d+eZ/UEsHCC03NyWUBwAA+ikAAFBLAQIUABQACAAIADtz5EBFzN5dGgAAABgAAAAWAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYV9qYXZhc2NyaXB0LmpzUEsBAhQAFAAIAAgAO3PkQC03NyWUBwAA+ikAAAwAAAAAAAAAAAAAAAAAXgAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAgACAH4AAAAsCAAAAAA=" showResetIcon = "false" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" /> | ||
| + | <br /> | ||
| + | --[[Benutzer:HecklF|Flo60]] 14:36, 4. Jul. 2012 (CEST) | ||
| + | |||
| + | ==Wie gehen wir vor?== | ||
| + | Das Verhältnis des Kreises mit dem Mittelpunkt (O|0) zum Quadrat <math>\overline{ACDE}</math> beträgt <math>\pi \ : \ 4</math> oder einfacher: <math>\frac{3} {4}</math> zu 1.<br /><br /> | ||
| + | Gleiches gilt für ein gleich großes Segment der beiden, also für ein viertel des Kreises und einem Viertel des Quadrates (man überzeuge sich durch Rechnung mit Variablen)<br /><br /> | ||
| + | ----- | ||
| + | Jetzt liegt die Fläche irgendwo zwischen den 2 Flächeneinheiten des hellblauen Quadrats (Seitenlänge nach Pythagoras <math>\sqrt{2}</math> und der Differenz aus den 4 FE des großen Quadrats und den 3 FE des Kreises, also 1.<br /><br /> | ||
| + | Offensichtlich sind wir näher an der 1, als an der Fläche 2 FE. | ||
| + | |||
| + | =Drehen - Strecken - etc.= | ||
| + | ==Wir wollen folgendermaße abbilden:== | ||
| + | <ggb_applet width="1000" height="647" version="4.0" ggbBase64="UEsDBBQACAAIADB25EAAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiu5QIAUEsHCEXM3l0aAAAAGAAAAFBLAwQUAAgACAAwduRAAAAAAAAAAAAAAAAADAAAAGdlb2dlYnJhLnhtbO1a63LbNhb+nT4FRj920k5s4U4yK6djO/FsZtyms+7u7OzObgciIQk1RaokJcuZPtT2FfoAfaYeACRFXRxbtpN4d6qJAxA4uJzvnPMdgNLg6+U0RQtdlCbPjnrkEPeQzuI8Mdn4qDevRgdh7+tXXwzGOh/rYaHQKC+mqjrqcStpEqjI4YiyUXwwlDw64CMqDyKlhgeKhwFVcSTDUPQQWpbmZZZ/q6a6nKlYX8QTPVXneawqt/CkqmYv+/2rq6vDZqnDvBj3x+Ph4bJMegi2mZVHvbryEqZbG3TFnDjFmPT/8c25n/7AZGWlslj3kFVhbl598WxwZbIkv0JXJqkmoDANQY+JNuMJKBWFvIf6VmoGiMx0XJmFLmFs59EpXU1nPSemMtv/zNdQ2urTQ4lZmEQXRz18SJkgQlKAIS+MzqpahtRr9ZtZBgujr/x0tubh7aEqz9OhsjOhn39GFFOMXtiC+IJCIaXvwr4NM19QX3BfCC/D/XDuRbmX4V6Gsx5amNIMU33UG6m0BOhMNirAbO1zWV2n2u2nblhpTV6ATqV5D8IMA64ea2jH+IX9k/DHbUd/XUnSWbUq5nsu2ixJqOR3X5M+SFO20pNsr0nFDXrKDyzqFb+ToqKDLSzl/rm/rRXZh9TcXNE/P2xBa4JPoOKg38TKoA4PVE6sbO0+lZ6WNmBYhERk/Z4gAcEhA3BzgUgERUARhAMiAnEBjyRE0pYBYgF0cMRQiKwcYchFhwjhPx64ySQSMJltDSAoEYGFOBIMERdUHEEoIReYEKSUgYQQSMAguzyhdgomEZfwxELEYY82JgMCggwGwjMsTxEjiNnBJEBUImnnI9zGugzt1mFKiiRGktgJIawhpH04g3yImNVG1nCZbDav1iCKp0lTrfJZawuQBkJa0Z0nqDU2fDZI1VCnkCEurCURWqjURoRbaJRnFWoD0reNCzWbmLi80FUFo0r0o1qoc1Xp5RlIl83aTjbOs/K7Iq9O83Q+zUqE4jzF7Z7zlHTqtN01PLBOB+92iE6H7NSDnevm0IPmpYb186JsxFWSvLUSK2oAJN9l6fVJodXlLDfragz6LtkM9DxOTWJU9ndwVruKxQWtco8Nlib3hCRqdpIXycV1CS6Mlv/URQ7YsuCQYEaDCBieyDCAcdd1F5WHJCJMRmHEqZAMskwZKxt9VJJDGQUkkjRgNgHZUbv7AlybTy9aI6mlbvUfFybp1t+WJ3matGg4AE7VrJoX7twA7FhYrY6zcaqdkzi+haQcXw7z5YX3Dubn+v56Bk/Yrz8cO+ARkAMVoMq4Loe+dDJ2Y60UdjLYSeDG3UzS9pOIOglXDn3ppMB//dZqRUmjJcHNMqZ0lIZ7a4HjnN9m+HlmqvPmoTLxZa0p8fLfzqdD3brQ+pTkkaYc9DdcbHCpi0yntUeDIef5vPQB2nH2RMdmCo++owZEWWP9DTbgWxM9LnSz79SdyDxcrhd3fXWr2U11VuTTt9nie/CEjQ0M+s0uB2VcmJn1NzSELHCpVz6VmFJBEkm642wIguqxTRYAT2WhgeCcV5O8cGcu4BQoneR0qrIEZS7vnM6LhT5VRaVLQKq3IkQF1BLn5fPqy/88Z1/CVEAvpclWz0AxFRTMeYECXmESf/Xrf72a+bxqJlFer3pZG/qpnsJRD1XOu2O7gbjdQGNw5bZiLYvy4Y9AsBsO0TEZ9N/g80ils4my58wa/VRd62LNHm66b/Jk3UqrCKiAnS/hDFq6MK3qgHSVv5gk0S4ze3fzam0paOdqtz38rGqpDHzbeQhQ6MzHzkxrH3WtbjOYznHVWg4Aby7R8qh34C5C1/WF6H13F3uDBqT6U+aHlD6a9XKWmthUH4bUkWqL2fEtmK5I5iZIHY9+RFDJbaDiDUxJswmnqU0KaycJ37rBLXeF62Qbruaw+T+El03m103lERBbZ8VzcOUTUwI4ebHBiceeCk+2eC7+MM+t0UB8mw0+Lg90ormDpPRI2qYggOvE6iMfL8DNdHeAb+O/gfuJx/14C/dkD9yTJ4S79LgftC7sKp8Y6LdZBacmAGID7cSjHW+hffphtNep5vR+VGPP/mNfDH3xcMBhaCRYwKP2IxsCkUEYNBYQXDwijZyaIk43Hfn0JgLRtxyU8szELXL683ryvTzUjHW2cJwKl9clrtPdNa7z3/umZUlcWNg+0uRE0qF4SB+FWaLjRv64kTqmzqAdI8MnhHZWL3HM3cwkWBeBDuFjcrNjZ2jZC78Zmfj+xmeoj0L0FXpt/FvYfx2/QCf/3vKI0T4eMfrDI27yCI4jiaM2+kP2mVziO8eO6x4x2rL6630o9vX9KJZQ/wbBlU/jRMdhLwGVNAgiIjghvObnkAQEmgXFIhShDedHP+7tsstwyy5n+9jl7F6XkoeY5d1oVOrKYmlfH9nLBNnHaBAC9zyISxkxTKIQ0yiUq2P5ZvOjW+02guVdgj19gc62CXa8D8GO/yDYGwmWYBmGnEpMGNRp8JkIdse9oXaIsy3bT/a4N0yeyr0BAouEDEsIKxIFFu063khIuvEmm6scCULGpcBRhAmPGP3kV7mbbhhjb5eJf5NIt8zzZh+2ffOULhqMQL6KAslDQSmznu4sxJnsNgcf4UWPe7nc6vzbLw4VGDivh9PDMIgC6wUiiLDkzX2zTO338WhqMmf7qQI95CENwdcEwwEJIhGCR6lhmafzSl/EhdbZ6hcKPrHVX90E1PGJ/fq3fqklXGVklp1X2JO8MO/zrFJrtrnne1GCtyOM3NF+5P7xoIq4Y7Ab0yoG5hOMRlSQKOJQEXd863pzTP01r1S1SXRvfECB1V1EnW5H1J/ULC//vFdc1UOeUHQRLIgknEsa8sg6ch1eEceh5BH4goRcJORHOHDshP3sNtjP9of97CGwP+rRfu0FSkjCkERACwFkE0po88qaRhxOeBwSeSBC/DjEdhfka5Qc/gfP7XHvt1/qb6Y6vr7LGPc2ydM0DJFBwDCkfSYlDiltDuERJH4iMPAPRA0N2Md4U57H83K3YbrmgfDYNMW7ooK8kxlNbjmIuRUaaDujHpAxBHm4BR72HeGjo0jvhSL9f0LxtUlv5GfieWH764Ma5h9u8cKdbPDDDif8rEzwKS/j/e5PDtwPe+pfp776HVBLBwg71LDRNgkAADorAABQSwECFAAUAAgACAAwduRARczeXRoAAAAYAAAAFgAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc1BLAQIUABQACAAIADB25EA71LDRNgkAADorAAAMAAAAAAAAAAAAAAAAAF4AAABnZW9nZWJyYS54bWxQSwUGAAAAAAIAAgB+AAAAzgkAAAAA" showResetIcon = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" /> | ||
| + | |||
| + | ==Hier kann man sich versuchen, den Streckfaktor und den Drehwinkel zu berechnen== | ||
| + | <ggb_applet width="1000" height="700" version="4.0" ggbBase64="UEsDBBQACAAIAG925EAAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiu5QIAUEsHCEXM3l0aAAAAGAAAAFBLAwQUAAgACABvduRAAAAAAAAAAAAAAAAADAAAAGdlb2dlYnJhLnhtbO1a/XIbtxH/23kKDP/oJBlLxDfuXMoZSbamnnHiTJV2Ou20GfAOJBEd75i7I0V58lDNK/QB8kxdAHfkkZQsUZJttROOZeCAxcf+dve3wJGDb5bTDC1MWdkiP+qRQ9xDJk+K1Objo968Hh1EvW9efjEYm2JshqVGo6Kc6vqox52kTaEihyPKRsnBUPL4gI+oPIi1Hh5oHimqk1hGkeghtKzsi7z4Tk9NNdOJOU8mZqrfFomu/cKTup696PcvLy8P26UOi3LcH4+Hh8sq7SHYZl4d9ZrKC5huY9Al8+IUY9L/27dvw/QHNq9qnSemh5wKc/vyi2eDS5unxSW6tGk9AYVpBHpMjB1PQKk44j3Ud1IzQGRmktouTAVjO49e6Xo663kxnbv+Z6GGspU+PZTahU1NedTDh5QJIiQFGIrSmrxuZEizVr+dZbCw5jJM52oB3h6qiyIbajcT+uUXRDHF6LkrSCgoFFKGLhzaMAsFDQUPhQgyPAznQZQHGR5kOOuhha3sMDNHvZHOKoDO5qMSzLZ6ruqrzPj9NA1rrclz0Kmy70GYYcA1YA3tGD93fxL+uOvobypJOqvW5XzPRdslCZX87mvSB2nK1nqS3TWpuEFP+YFFg+J3UlR0sIWl/D//t7Mi+5Ca2yuG54ct6EzwCVQc9NtYGTThgaqJk23cpzbTygUMi5GInd8TJCA4pAI3F4jEUCiKIBwQEYgLeCQRkq5UiCno4IihCDk5wpCPDhHBf1z5ySQSMJlrVRCUiMBCHAmGiA8qjiCUkA9MCFLKQEIIJGCQW55QNwWTiEt4YhHisEcXk4qAIIOB8AzLU8QIYm4wUYhKJN18hLtYl5HbOkxJkcRIEjchhDWEdAhnkI8Qc9rIBi6bz+b1BkTJNG2rdTFb2QKkgZDWdBcIaoMNnw0yPTQZZIhzZ0mEFjpzEeEXGhV5jVYBGdrGpZ5NbFKdm7qGURX6SS/0W12b5RlIV+3aXjYp8ur7sqhPi2w+zSuEkiLDqz0XGenU6WrX8MA6HbzbITodslNX165bQA+aVwbWL8qqFddp+sZJrKkBkHyXZ1cnpdEXs8JuqjHo+2QzMPMks6nV+V/BWd0qDhe0zj0uWNrcE5G43UlRpudXFbgwWv7dlAVgy9QhwYyqGBieyEjBuKumi8pDEhMm4yjmVEgGWaZKtIs+KsmhjBWJJVXMJSA36vo+hRvzmcXKSHppVvqPS5t262+qkyJLV2h4AE71rJ6X/twA7Fg6rY7zcWa8k3i+haScXAyL5XnwDhbm+uFqBk84rD8ce+ARkAMVoMq4KYeh9DJuYysp7GWwl8Ctu9l01U9i6iV8OQyllwL/DVtrFCWtlgS3y9jKUxrubQSOd36X4ee5rd+2D7VNLhpNSZD/bj4dmpULbU5JHmnKQX/LxQYXpsxN1ng0GHJezKsQoB1nT01ip/AYOhpAtDPWX2ADoTU149K0+878iSzA5Xtx11d3mv1UZ2UxfZMvfgBP2NrAoN/uclAlpZ05f0NDyAIXZu1Tqa00JJG0O86FIKieuGQB8NQOGgjOeT0pSn/mAk6B0ktOpzpPUe7zzum8XJhTXdamAqR6a0LUQC1JUX1Zf/WvL9lXMBXQS2Xz9TNQTA0F816ggVeYxF//599BzWJet5PooFezrAv9zEzhqIdq792J20Cy2kBrcO234iyLiuFPQLBbDtExGfTf4PNIZ7OJdufMBv1MX5lywx5+um+LdNNK6wiogZ0v4Axa+TCtm4D0lT/ZNDU+Mwd3C2rtKOjmWm17+FnV0jn4tvcQoNBZiJ2ZMSHqVrrNYDrPVRs5ALy5Qsuj3oG/CF01F6L33V3sDRqQ6s95GFKFaDbLWWYTW38YUk+qK8yOb8F0TTI3Qep59COCSm4DFW9hStpNeE1dUtg4SYTWLW65K1wnu3C1h83/IbxcMr9qK4+A2CYrvgVXPrEVgFOUW5x4HKjwZIfnkg/z3AYNJLfZ4OPyQCeaO0jKgKRrUgquE+uPfLwAt9PrA3wX/y3cTwLuxzu4p3vgnj4h3GXA/WDlwr7yiYF+k9dwagIgttBOA9rJDtqnH0Z7k2pO70c17uw/DsUwFA8HHIbGgikerz6yJRCpItVaQHDxiDRyassk23bk05sIxNxyUCpym6yQM5/Xk+/loXZs8oXnVLi8LnGT7q5wk//ety1L4sPC9ZE2J5IOxUP6KO0SHbfyx63UMfUG7RgZPhG0s2aJY+5nJmpTBDpEiMntjmtDy1347cgm9zc+Q30Uoa/RKxvewv7j+Dk6+eeOR4z28YjR7x5xk0dwHEscr6I/Yp/JJb737LjpEaMdq7/ah2Jf3Y9iCQ1vEHz5NE50HPaiqKRKxURwQnjDzxFRBJoFxSISkQvnRz/uXWeX4Y5dzvaxy9m9LiUPMcu70agytcPSvT5ylwmyj9EgBO55EJcyZpjEEaZxJNfH8u3mR7fabQTLuwR7+hyd7RLseB+CHf9OsDcSLMEyijiVmDCoU/WZCPaae0PjEGc7tp/scW+YPJV7AwQWiRiWEFYkVg7tJt5IRLrxJturHFER41LgOMaEx4x+8qvcTTeMcbDLJLxJpDvmeb0P275+ShcNRiBfxUrySFDKnKd7C3Emu83qI7zo8S+XVzr/9qtHBQbOm+H0MFKxcl4gVIwlb++bVea+j0dTm3vbTzXoIQ9pBL4mGFZExSICj9LDqsjmtTlPSmPy9S8UQmJrvrpR1POJ+/q3eaklfGVkl51X2JOitO+LvNYbtrlvgBG8G2LkjgYk9w8IXSYdi92YVzFQn2A0poLEMYeKuONr15uD6s9FrettpnsdIgrM7kPqdDek/qBnRfXHvQKrGfKEwotgQSThXNKIx86Tm/iKOY4kj8EXJCQjIT/CieNa2M9ug/1sf9jPHgL7o57tN96gRCSKSAy8oCCdUELbd9Y05nDE45DJlYjw4zDbXZBvUPL4H3zpznu//dp8NdXx9euMcW+TPE3DEKkUw5D3mZQ4orQ9hceQ+YnAwD8QNVSxj/GqvEjm1fWG6ZoHwmPbFO/KGhJPbg255STmV2ih7Yx6SMoQ5OEmeNi3hI8OI70XjPT/CsZXNruRoUlght1vEBqcf7zFD6/lgx9vdcNPzAWf8j7e7/7qwP+2p/mB6sv/AlBLBwgV/lFONgkAAD0rAABQSwECFAAUAAgACABvduRARczeXRoAAAAYAAAAFgAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc1BLAQIUABQACAAIAG925EAV/lFONgkAAD0rAAAMAAAAAAAAAAAAAAAAAF4AAABnZW9nZWJyYS54bWxQSwUGAAAAAAIAAgB+AAAAzgkAAAAA" showResetIcon = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "true" showToolBarHelp = "false" showAlgebraInput = "true" useBrowserForJS = "true" allowRescaling = "true" /> | ||
| + | |||
| + | ==Wie kommen wir auf die Lösung?== | ||
| + | [[Lösung 04.07.2012: Streckung - Drehung]] | ||
=Zurück zur Übersichtsseite= | =Zurück zur Übersichtsseite= | ||
Aktuelle Version vom 4. Juli 2012, 13:52 Uhr
Inhaltsverzeichnis |
Original oder Fälschung?
Welche der beiden Kurven ist eine Asteroidenkurve?
--Flo60 14:16, 4. Jul. 2012 (CEST)
Begründung
Berechne Punkt F
Man schätze die Fläche der Asteroide
Folgende Applikation kann behilflich sein:
--Flo60 14:36, 4. Jul. 2012 (CEST)
Wie gehen wir vor?
Das Verhältnis des Kreises mit dem Mittelpunkt (O|0) zum Quadrat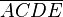 
beträgt 
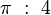oder einfacher: 
zu 1.
Gleiches gilt für ein gleich großes Segment der beiden, also für ein viertel des Kreises und einem Viertel des Quadrates (man überzeuge sich durch Rechnung mit Variablen)
Jetzt liegt die Fläche irgendwo zwischen den 2 Flächeneinheiten des hellblauen Quadrats (Seitenlänge nach Pythagoras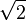 
und der Differenz aus den 4 FE des großen Quadrats und den 3 FE des Kreises, also 1.
Offensichtlich sind wir näher an der 1, als an der Fläche 2 FE.
Drehen - Strecken - etc.
Wir wollen folgendermaße abbilden:
Hier kann man sich versuchen, den Streckfaktor und den Drehwinkel zu berechnen
Wie kommen wir auf die Lösung?
Lösung 04.07.2012: Streckung - Drehung
