Lösung von Aufg. 11.1 S: Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
 
(19 dazwischenliegende Versionen von 5 Benutzern werden nicht angezeigt)
Zeile 1: Zeile 1:
−
Definitionsversuch 1<br />
+
== Aufgabe 11.1 ==
 +
Definieren Sie die Begriffe ''Innenwinkel eines Dreiecks'' und ''Außenwinkel eines Dreiecks''.<br /><br />
 +
 
 +
 
 +
 
 +
==Definitionsversuch 1, Tchu Tcha Tcha==
 
(Innenwinkel eines Dreiecks):<br />
 
(Innenwinkel eines Dreiecks):<br />
 
Es sei <math>\overline{ABC}</math> ein Dreieck. Die Winkel <math>\angle ABC , \angle BCA  und \angle CAB</math> sind die Innenwinkel des Dreiecks <math>\overline{ABC}</math>.<br />
 
Es sei <math>\overline{ABC}</math> ein Dreieck. Die Winkel <math>\angle ABC , \angle BCA  und \angle CAB</math> sind die Innenwinkel des Dreiecks <math>\overline{ABC}</math>.<br />
 
<br />
 
<br />
 
(Außenwinkel eines Dreiecks):<br />
 
(Außenwinkel eines Dreiecks):<br />
−
Ein Winkel, dessen Nebenwinkel ein Innenwinkel eines Dreiecks ist, nennt man Außenwinkel dieses Dreiecks.<br />--[[Benutzer:Nummero6|Tchu Tcha Tcha]] 12:35, 5. Jul. 2012 (CEST)
+
Ein Winkel, dessen Nebenwinkel ein Innenwinkel eines Dreiecks ist, nennt man Außenwinkel dieses Dreiecks.<br />--[[Benutzer:Nummero6|Tchu Tcha Tcha]] 12:35, 5. Jul. 2012 (CEST)<br />
 +
==Definitionsversuch 2, Wurzel==
 +
 
 +
 
 +
 
 +
ABC sei Dreieck.die Strahlen AC+ und AB+ bilden zusammen mit dem Scheitelpunkt S denn Innenwinkel  Alpha. Bei innenenwinkel ist der Betrag < 180. Der nebenwinkel von Alpha heißt Außenwinkel Alpha '. Als gemeinsamen Schenkel hat der Außenwinkel den Strahl CA- oder AB-.
 +
--[[Benutzer:Wurzel|H2O]] 13:47, 8. Jul. 2012 (CEST)
 +
 
 +
===M.G.===
 +
Warum so kompliziert? Wenn Sie das Dreieck durch seine Eckpunkte bereits gekennzeichnet haben, dann können Sie doch die Innenwinkel in der Form <math>\angle Punkt_1, Scheitelpunkt, Punkt_2</math> kennzeichnen. Die Angabe zu den Größen hat in der Definition nichts verloren. Zu jedem Innenwinkel gehören zwei Außenwinkel. Wenn Sie über den Begriff des Nebenwinkels Außenwinkel definiert haben, dann hat die Angabe der gemeinsamen Schenkel in der Definition nichts mehr verloren.--[[Benutzer:*m.g.*|*m.g.*]] 19:46, 8. Jul. 2012 (CEST)
 +
 
 +
== Definitionsversuch Michael==
 +
es liegt ein Dreieck mit schulüblichen Bezeichnungen (ABC) vor:
 +
Die Winkel <ABC, <ACB, <BAC nennt man Innenwinkel eines Dreiecks.
 +
Die Winkel die <ABC, <ACB, <BAC jeweils zu 360° ergänzen nennt man Außenwinkel eines Dreiecks.
 +
 
 +
--[[Benutzer:Michael|Michael]] 21:33, 10. Jul. 2012 (CEST)
 +
===Bemerkungen M.G.===
 +
====Innenwinkel====
 +
# Die schulüblichen Bezeichnungen brauchen Sie hier nicht wirklich: Es sei <math>\overline{ABC}</math> ein Dreieck.
 +
# Korrekt ist: Die Winkel <math>\angle ABC, \angle ACB, \angle BAC</math> nennt man Innenwinkel ...
 +
# Jetzt geht es nicht ganz korrekt weiter: ... '''eines''' Dreiecks. Nachdem eine beliebiges aber festes Dreieck <math>\overline{ABC}</math> ausgewählt wurde, sind unsere Winkel <math>\angle ABC, \angle ACB, \angle BAC</math> die Innenwinkel gerade dieses ausgewählten Dreiecks <math>\overline{ABC}</math> und nicht irgendeines beliebigen weiteren Dreiecks. Also korrekt muss es heißen: ... nennt man Innenwinkel '''des''' Dreiecks. (<math>\overline{ABC}</math>) Hier muss also der ''bestimmte'' Artikel verwendet werden und nicht der unbestimmte.
 +
====Außenwinkel====
 +
Sie schreiben: ''Die Winkel die <ABC, <ACB, <BAC jeweils zu 360° ergänzen nennt man Außenwinkel eines Dreiecks.''
 +
Die Definition ist so nicht korrekt. Ich übergebe Ihre Definition mal der allgemeinen Diskussion.
 +
==Diskussion zur Außenwinkeldefinition von Michael==
 +
===Die Definition===
 +
User Michael definierte (Korrektur der Wahl des Artikels vor Dreieck bereits durch M.G. durchgeführt):<br /><br />
 +
:::Die Winkel die <math>\angle ABC, \angle ACB, \angle BAC</math> jeweils zu 360° ergänzen nennt man Außenwinkel des Dreiecks <math>\overline{ABC}</math>
 +
===M.G.===
 +
 
 +
Diskutieren Sie die Definition von Michael. Was meint User Michael eigentlich? Warum liefert die Idee von User Michael keine korrekte Definition des Begriffs Außenwinkel eines Dreiecks?
 +
--[[Benutzer:*m.g.*|*m.g.*]] 22:37, 10. Jul. 2012 (CEST)
 +
 
 +
===Sissy66===
 +
Es kann nur der Nebenwinkel, von Alpha gesehen, nach unten liegende Winkel sein und der links davon.
 +
Der Winkel der ihn schließlich zu 360 Grad als Vollwinkel schließt, wäre der Scheitelwinkel zum Innenwinkel Alpha.--[[Benutzer:Sissy66|Sissy66]] 23:02, 10. Jul. 2012 (CEST)
 +
 
 +
====M.G.====
 +
Das Wort ''jeweils'' könnte darauf hin deuten, dass User Michael meint, jeder Winkel, der etwa den Innenwinkel <math>\alpha</math> zu 360° ergänzt ist Außenwinkel. Das wären dann zusammen die beiden Nebenwinkel von <math>\alpha</math> und der Scheitelwinkel von <math>\alpha</math>. Meinen Sie diese drei Winkel?
 +
 
 +
Rechts, links, unten, oben sind nur bedingt tauglich die Dinge zu beschreiben.--[[Benutzer:*m.g.*|*m.g.*]] 07:02, 11. Jul. 2012 (CEST)
 +
 
 +
<br/>
 +
Wahrscheinlich meint Michael das richtige. Aber ich würde es so verstehen, dass er die Vereinigung (?) der beiden Außenwinkel (von Alpha)+ dem Scheitelwinkel (von Alpha) als ein Winkel bezeichnet und dieser der Außenwinkel von Alpha sein soll. Das wäre dann nicht korrekt :)--[[Benutzer:RitterSport|RitterSport]] 12:15, 11. Jul. 2012 (CEST)
 +
 
 +
 
 +
 
 +
 
 +
 
 +
 
 +
[[Kategorie:Einführung_S]]

Aktuelle Version vom 11. Juli 2012, 11:15 Uhr

Inhaltsverzeichnis

Aufgabe 11.1

Definieren Sie die Begriffe Innenwinkel eines Dreiecks und Außenwinkel eines Dreiecks.


Definitionsversuch 1, Tchu Tcha Tcha

(Innenwinkel eines Dreiecks):
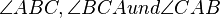Es sei \overline{ABC} ein Dreieck. Die Winkel \angle ABC , \angle BCA und \angle CAB sind die Innenwinkel des Dreiecks \overline{ABC}.

(Außenwinkel eines Dreiecks):
Ein Winkel, dessen Nebenwinkel ein Innenwinkel eines Dreiecks ist, nennt man Außenwinkel dieses Dreiecks.
--Tchu Tcha Tcha 12:35, 5. Jul. 2012 (CEST)

Definitionsversuch 2, Wurzel

ABC sei Dreieck.die Strahlen AC+ und AB+ bilden zusammen mit dem Scheitelpunkt S denn Innenwinkel Alpha. Bei innenenwinkel ist der Betrag < 180. Der nebenwinkel von Alpha heißt Außenwinkel Alpha '. Als gemeinsamen Schenkel hat der Außenwinkel den Strahl CA- oder AB-. --H2O 13:47, 8. Jul. 2012 (CEST)

M.G.

Warum so kompliziert? Wenn Sie das Dreieck durch seine Eckpunkte bereits gekennzeichnet haben, dann können Sie doch die Innenwinkel in der Form 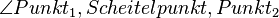\angle Punkt_1, Scheitelpunkt, Punkt_2 kennzeichnen. Die Angabe zu den Größen hat in der Definition nichts verloren. Zu jedem Innenwinkel gehören zwei Außenwinkel. Wenn Sie über den Begriff des Nebenwinkels Außenwinkel definiert haben, dann hat die Angabe der gemeinsamen Schenkel in der Definition nichts mehr verloren.--*m.g.* 19:46, 8. Jul. 2012 (CEST)

Definitionsversuch Michael

es liegt ein Dreieck mit schulüblichen Bezeichnungen (ABC) vor: Die Winkel <ABC, <ACB, <BAC nennt man Innenwinkel eines Dreiecks. Die Winkel die <ABC, <ACB, <BAC jeweils zu 360° ergänzen nennt man Außenwinkel eines Dreiecks.

--Michael 21:33, 10. Jul. 2012 (CEST)

Bemerkungen M.G.

Innenwinkel

  1. Die schulüblichen Bezeichnungen brauchen Sie hier nicht wirklich: Es sei \overline{ABC} ein Dreieck.
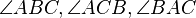  2. Korrekt ist: Die Winkel \angle ABC, \angle ACB, \angle BAC nennt man Innenwinkel ...
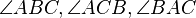  3. Jetzt geht es nicht ganz korrekt weiter: ... eines Dreiecks. Nachdem eine beliebiges aber festes Dreieck \overline{ABC} ausgewählt wurde, sind unsere Winkel \angle ABC, \angle ACB, \angle BAC die Innenwinkel gerade dieses ausgewählten Dreiecks \overline{ABC} und nicht irgendeines beliebigen weiteren Dreiecks. Also korrekt muss es heißen: ... nennt man Innenwinkel des Dreiecks. (\overline{ABC}) Hier muss also der bestimmte Artikel verwendet werden und nicht der unbestimmte.

Außenwinkel

Sie schreiben: Die Winkel die <ABC, <ACB, <BAC jeweils zu 360° ergänzen nennt man Außenwinkel eines Dreiecks. Die Definition ist so nicht korrekt. Ich übergebe Ihre Definition mal der allgemeinen Diskussion.

Diskussion zur Außenwinkeldefinition von Michael

Die Definition

User Michael definierte (Korrektur der Wahl des Artikels vor Dreieck bereits durch M.G. durchgeführt):

Die Winkel die 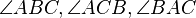\angle ABC, \angle ACB, \angle BAC jeweils zu 360° ergänzen nennt man Außenwinkel des Dreiecks \overline{ABC}

M.G.

Diskutieren Sie die Definition von Michael. Was meint User Michael eigentlich? Warum liefert die Idee von User Michael keine korrekte Definition des Begriffs Außenwinkel eines Dreiecks? --*m.g.* 22:37, 10. Jul. 2012 (CEST)

Sissy66

Es kann nur der Nebenwinkel, von Alpha gesehen, nach unten liegende Winkel sein und der links davon. Der Winkel der ihn schließlich zu 360 Grad als Vollwinkel schließt, wäre der Scheitelwinkel zum Innenwinkel Alpha.--Sissy66 23:02, 10. Jul. 2012 (CEST)

M.G.

Das Wort jeweils könnte darauf hin deuten, dass User Michael meint, jeder Winkel, der etwa den Innenwinkel \alpha zu 360° ergänzt ist Außenwinkel. Das wären dann zusammen die beiden Nebenwinkel von \alpha und der Scheitelwinkel von \alpha. Meinen Sie diese drei Winkel?

Rechts, links, unten, oben sind nur bedingt tauglich die Dinge zu beschreiben.--*m.g.* 07:02, 11. Jul. 2012 (CEST)


Wahrscheinlich meint Michael das richtige. Aber ich würde es so verstehen, dass er die Vereinigung (?) der beiden Außenwinkel (von Alpha)+ dem Scheitelwinkel (von Alpha) als ein Winkel bezeichnet und dieser der Außenwinkel von Alpha sein soll. Das wäre dann nicht korrekt :)--RitterSport 12:15, 11. Jul. 2012 (CEST)

Von „http://geometrie.zum.de/index.php?title=Lösung_von_Aufg._11.1_S&oldid=16464“