Lösung von Testaufgabe 2.1 SS12: Unterschied zwischen den Versionen
| (9 dazwischenliegende Versionen von 8 Benutzern werden nicht angezeigt) | |||
| Zeile 4: | Zeile 4: | ||
Es seien A,B,C,D vier Punkte. Die Punkte A,B,C,D seien komplanar und jeweils zwei von ihnen kollinear. Die Vereinigungsmenge der Strecken AB,BC,CD,AD bilden das Viereck ABCD.--[[Benutzer:Celebino|Celebino]] 11:44, 14. Jul. 2012 (CEST) | Es seien A,B,C,D vier Punkte. Die Punkte A,B,C,D seien komplanar und jeweils zwei von ihnen kollinear. Die Vereinigungsmenge der Strecken AB,BC,CD,AD bilden das Viereck ABCD.--[[Benutzer:Celebino|Celebino]] 11:44, 14. Jul. 2012 (CEST) | ||
| + | |||
| + | Ist beides nicht ganz korrekt.--[[Benutzer:*m.g.*|*m.g.*]] 14:20, 14. Jul. 2012 (CEST) | ||
| + | |||
| + | Es seien A,B,C,D vier kollineare Punkte, von denen zwei jeweils paarweise kollinear sind. | ||
| + | Eine Figur mit der Vereinigungsmenge aus <math>\overline{AB} </math>, <math>\overline{BC} </math>, <math>\overline{CD} </math>, <math>\overline{DA} </math>, ist ein Viereck.--[[Benutzer:Mahe84|Mahe84]] 17:04, 14. Jul. 2012 (CEST) | ||
| + | |||
| + | Es seien A, B, C und D vier paarweise verschiedene Pnkte ein und derselben Ebene. JE drei der Punkte seien nich kollinear. Die Vereinigungsmenge der Strecken <math>\overline{AB} </math>, <math>\overline{BC} </math>, <math>\overline{CD} </math> und <math>\overline{DA} </math> heißt Viereck.--[[Benutzer:*osterhase*|*osterhase*]] 17:23, 14. Jul. 2012 (CEST) | ||
| + | |||
| + | Es seien A,B,C,D komplanare Punkte ,die jeweils durch Strecken mit je zwei verschieden Punkten verbunden sind, drei aufeinander folgende Punkte seien nicht kollinear.Die Vereinigungsmenge der Strecken <math>\overline{AB} </math>, <math>\overline{BC} </math>, <math>\overline{CD} </math> und <math>\overline{DA} </math> heißt Viereck.--[[Benutzer:Just noch ein sailA|Just noch ein sailA]] 17:57, 14. Jul. 2012 (CEST)<br /> | ||
| + | |||
| + | Es seien A,B,C,D vier nicht identische Punkte in ein und derselben Ebene, von denen jeweils höchstens 2 Punkte zueinander kollinear sind. | ||
| + | Die Vereinigungsmenge der Strecken <math>\overline{AB} ,\overline{BC} ,\overline{CD} und \overline{DA} </math> nennt man Viereck <math>\overline{ABCD}</math>.<br />--[[Benutzer:Nummero6|Tchu Tcha Tcha]] 18:18, 14. Jul. 2012 (CEST) | ||
| + | |||
| + | Es seien A,B,C,D vier Punkte für die gilt: komp(A,B,C,D) und mind 3 dieser Punkte sind nkoll und A,B,C,D sind paarweise verschieden. Die Menge aller Punkte für die gilt <math>\overline{AB} </math> vereinigt mit <math>\overline{BC} </math> vereinigt mit <math>\overline{CD}</math> vereinigt mit <math> \overline{DA} </math>, nennt man Viereck <math>\overline{ABCD}</math>.--[[Benutzer:LuLu7410|LuLu7410]] 18:50, 14. Jul. 2012 (CEST) | ||
| + | |||
| + | Wenn eine Figur aus vier komplanaren Strecken besteht, wobei jeweils höchstens 2 ihrer Anfangs- und/oder Endpunkte zueinander kollinear sind und für die gilt, dass jeweils zwei dieser Strecken nur einen Punkt, entweder ihren Anfangs- oder Endpunkt, gemeinsam haben, so ist diese Figur ein Viereck.--[[Benutzer:Butterbrot|Butterbrot]] 19:52, 14. Jul. 2012 (CEST) | ||
| + | <br/> | ||
| + | |||
| + | Muss man unter Umständen noch darauf achten, dass sich die Strecken nicht schneiden? Weil so ein "Sanduhrmäßiges" Ding wäre ja kein 4-Eck, oder?!--[[Benutzer:RitterSport|RitterSport]] 17:16, 22. Jul. 2012 (CEST) | ||
Aktuelle Version vom 22. Juli 2012, 17:17 Uhr
Es seien A,B,C,D vier Punkte die alle in einer Ebene liegen und nicht kollinear sind.
Unter dem Viereck ABCD versteht man die Punktmenge: 
vereinigt mit 
vereinigt mit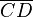 
vereinigt mit 
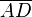--Funkdocta 11:33, 14. Jul. 2012 (CEST)
Es seien A,B,C,D vier Punkte. Die Punkte A,B,C,D seien komplanar und jeweils zwei von ihnen kollinear. Die Vereinigungsmenge der Strecken AB,BC,CD,AD bilden das Viereck ABCD.--Celebino 11:44, 14. Jul. 2012 (CEST)
Ist beides nicht ganz korrekt.--*m.g.* 14:20, 14. Jul. 2012 (CEST)
Es seien A,B,C,D vier kollineare Punkte, von denen zwei jeweils paarweise kollinear sind.
Eine Figur mit der Vereinigungsmenge aus , , , 
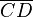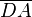, ist ein Viereck.--Mahe84 17:04, 14. Jul. 2012 (CEST)
Es seien A, B, C und D vier paarweise verschiedene Pnkte ein und derselben Ebene. JE drei der Punkte seien nich kollinear. Die Vereinigungsmenge der Strecken , , 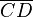und 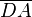heißt Viereck.--*osterhase* 17:23, 14. Jul. 2012 (CEST)
Es seien A,B,C,D komplanare Punkte ,die jeweils durch Strecken mit je zwei verschieden Punkten verbunden sind, drei aufeinander folgende Punkte seien nicht kollinear.Die Vereinigungsmenge der Strecken , , 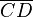und 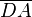heißt Viereck.--Just noch ein sailA 17:57, 14. Jul. 2012 (CEST)
Es seien A,B,C,D vier nicht identische Punkte in ein und derselben Ebene, von denen jeweils höchstens 2 Punkte zueinander kollinear sind.
Die Vereinigungsmenge der Strecken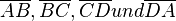 
nennt man Viereck 
.
--Tchu Tcha Tcha 18:18, 14. Jul. 2012 (CEST)
Es seien A,B,C,D vier Punkte für die gilt: komp(A,B,C,D) und mind 3 dieser Punkte sind nkoll und A,B,C,D sind paarweise verschieden. Die Menge aller Punkte für die gilt vereinigt mit vereinigt mit 
vereinigt mit 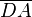, nennt man Viereck .--LuLu7410 18:50, 14. Jul. 2012 (CEST)
Wenn eine Figur aus vier komplanaren Strecken besteht, wobei jeweils höchstens 2 ihrer Anfangs- und/oder Endpunkte zueinander kollinear sind und für die gilt, dass jeweils zwei dieser Strecken nur einen Punkt, entweder ihren Anfangs- oder Endpunkt, gemeinsam haben, so ist diese Figur ein Viereck.--Butterbrot 19:52, 14. Jul. 2012 (CEST)
Muss man unter Umständen noch darauf achten, dass sich die Strecken nicht schneiden? Weil so ein "Sanduhrmäßiges" Ding wäre ja kein 4-Eck, oder?!--RitterSport 17:16, 22. Jul. 2012 (CEST)
