Lösung von Testaufgabe 2.2 SS12: Unterschied zwischen den Versionen
Monsta (Diskussion | Beiträge) |
|||
| (13 dazwischenliegende Versionen von 7 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | Es sei s eine Gerade die den Kreis k zweimal schneidet, dann nennt man diese eine Sekante. Peach22 | + | Es sei s eine Gerade die den Kreis k zweimal schneidet, dann nennt man diese eine Sekante. Peach22<br /> |
| − | + | @Peach Vom Inhalt her fast korrekt. Vom Deutschen her erwartet man bei dann auch ein wenn. Machen Sie eine Konventionaldefinition draus. Ansonsten ist Sekante sein eine zweistellige Relation, die eine Gerade zu eine Kreis in Bezug setzt. Sie sollten diese Bezüglichkeit in der Definition noch deutlicher formulieren. | |
Es sei k ein Kreis und g eine Gerade. Ist der Abstand von g zum Kreismittelpunkt M kleiner als der Radius r des Kreises, | Es sei k ein Kreis und g eine Gerade. Ist der Abstand von g zum Kreismittelpunkt M kleiner als der Radius r des Kreises, | ||
| − | so nennt man die Gerade g Sekante des Kreises k. --[[Benutzer:Funkdocta|Funkdocta]] 11:29, 14. Jul. 2012 (CEST) | + | so nennt man die Gerade g Sekante des Kreises k. --[[Benutzer:Funkdocta|Funkdocta]] 11:29, 14. Jul. 2012 (CEST)<br /> |
| + | @Funkdocta: Vorsicht, wenn nichts weiter dabei steht, sind wir im Raum.--[[Benutzer:*m.g.*|*m.g.*]] 14:25, 14. Jul. 2012 (CEST) | ||
| + | |||
| + | Es sei k ein Kreis und s eine Gerade. Wenn die Gerade s den Kreis k in genau zwei Punkten schneidet und mit k in der selben Ebene liegt, dann ist s die Sekante des kreises k.--[[Benutzer:Celebino|Celebino]] 11:51, 14. Jul. 2012 (CEST)<br /> | ||
| + | @Celebino Warum so viel? Halten Sie die Definition minimal.--[[Benutzer:*m.g.*|*m.g.*]] 14:25, 14. Jul. 2012 (CEST) | ||
| + | |||
| + | Eine Gerade s, die den Kreis k, in zwei Punkten, welche nicht nebeneinander auf dem Kreis liegen, schneidet, ist eine Sekante. --[[Benutzer:Cermaka|Cermaka]] 15:28, 14. Jul. 2012 (CEST)<br /> | ||
| + | @Cermaka: Was heißt zwei Punkte liegen nicht nebeneinander auf dem Kreis?--[[Benutzer:*m.g.*|*m.g.*]] 22:55, 14. Jul. 2012 (CEST)<br /> | ||
| + | @m.g.: ich habe mit ,,nicht nebeneinander" gemeint, dass noch mindestens ein Punkt zwischen dem ersten geschnittenen und dem zweiten geschnittenen Punkt liegt; allerdings merke ich gerade, dass diese Information glaube ich unwichtig ist und die 2 Punkte, welche geschnitten werden doch nebeneinander liegen dürfen. Ich würde nun also eher sagen = Eine Gerade s, die den Kreis k, in 2 verschiedenen Punkten schneidet, ist eine Sekante. -Oder bin ich nun auf der völlig falschen Fährte?--[[Benutzer:Cermaka|Cermaka]] 01:16, 15. Jul. 2012 (CEST) | ||
| + | |||
| + | |||
| + | Es seien s eine Gerade und k ein Kreis der Ebene E. | ||
| + | Wenn die Gerade s zwei gemeinsame Schnittpunkte mit dem Kreis k besitzt, dann ist die Geade s eine Sekante des Kreises k.--[[Benutzer:Mahe84|Mahe84]] 17:16, 14. Jul. 2012 (CEST) | ||
| + | |||
| + | Es sei k ein Kreis. Die Gerade s, die mit k zwei Punkte A und B gemeinsam hat, heißt Sekante bezüglich k. | ||
| + | --[[Benutzer:*osterhase*|*osterhase*]] 17:26, 14. Jul. 2012 (CEST) | ||
| + | Es sei k ein Kreis und A, B zwei Punkte auf k mit A ist ungleich B. Die Gerade s, die durch die Punkte A und B geht, heißt Sekante bezüglich k.--[[Benutzer:*osterhase*|*osterhase*]] 17:26, 14. Jul. 2012 (CEST) | ||
| + | <br /> | ||
| + | |||
| + | Es sei s eine Gerade und k ein Kreis in ein und derselben Ebene. Wenn gilt: <math>\left|\ s \cap k \right| = 2</math> , dann ist die Gerade s eine Sekante bzgl. des Kreises k.--[[Benutzer:Nummero6|Tchu Tcha Tcha]] 18:23, 14. Jul. 2012 (CEST) | ||
| + | |||
| + | Es sei K ein Kreis und s eine Gerade. Kreis K und Gerade s gehören ein und der selben Ebene E an. Wenn die Gerade s den Kreis K in zwei beliebigen Punkten A,B schneidet, die nicht identisch sind, dann ist die Gerade s eine Sekante des Kreises K. --[[Benutzer:LuLu7410|LuLu7410]] 18:58, 14. Jul. 2012 (CEST) | ||
| − | + | Wenn eine Gerade den Kreis zweimal schneidet, so liegt diese Gerade automatisch in der Ebene, das muss nicht nochmal extra erwähnt werden, oder? Das war doch nur bei der einen speziellen Definition mit dem Radius! <br />--[[Benutzer:Monsta|Monsta]] 20:43, 17. Jul. 2012 (CEST) | |
Aktuelle Version vom 17. Juli 2012, 19:43 Uhr
Es sei s eine Gerade die den Kreis k zweimal schneidet, dann nennt man diese eine Sekante. Peach22
@Peach Vom Inhalt her fast korrekt. Vom Deutschen her erwartet man bei dann auch ein wenn. Machen Sie eine Konventionaldefinition draus. Ansonsten ist Sekante sein eine zweistellige Relation, die eine Gerade zu eine Kreis in Bezug setzt. Sie sollten diese Bezüglichkeit in der Definition noch deutlicher formulieren.
Es sei k ein Kreis und g eine Gerade. Ist der Abstand von g zum Kreismittelpunkt M kleiner als der Radius r des Kreises,
so nennt man die Gerade g Sekante des Kreises k. --Funkdocta 11:29, 14. Jul. 2012 (CEST)
@Funkdocta: Vorsicht, wenn nichts weiter dabei steht, sind wir im Raum.--*m.g.* 14:25, 14. Jul. 2012 (CEST)
Es sei k ein Kreis und s eine Gerade. Wenn die Gerade s den Kreis k in genau zwei Punkten schneidet und mit k in der selben Ebene liegt, dann ist s die Sekante des kreises k.--Celebino 11:51, 14. Jul. 2012 (CEST)
@Celebino Warum so viel? Halten Sie die Definition minimal.--*m.g.* 14:25, 14. Jul. 2012 (CEST)
Eine Gerade s, die den Kreis k, in zwei Punkten, welche nicht nebeneinander auf dem Kreis liegen, schneidet, ist eine Sekante. --Cermaka 15:28, 14. Jul. 2012 (CEST)
@Cermaka: Was heißt zwei Punkte liegen nicht nebeneinander auf dem Kreis?--*m.g.* 22:55, 14. Jul. 2012 (CEST)
@m.g.: ich habe mit ,,nicht nebeneinander" gemeint, dass noch mindestens ein Punkt zwischen dem ersten geschnittenen und dem zweiten geschnittenen Punkt liegt; allerdings merke ich gerade, dass diese Information glaube ich unwichtig ist und die 2 Punkte, welche geschnitten werden doch nebeneinander liegen dürfen. Ich würde nun also eher sagen = Eine Gerade s, die den Kreis k, in 2 verschiedenen Punkten schneidet, ist eine Sekante. -Oder bin ich nun auf der völlig falschen Fährte?--Cermaka 01:16, 15. Jul. 2012 (CEST)
Es seien s eine Gerade und k ein Kreis der Ebene E.
Wenn die Gerade s zwei gemeinsame Schnittpunkte mit dem Kreis k besitzt, dann ist die Geade s eine Sekante des Kreises k.--Mahe84 17:16, 14. Jul. 2012 (CEST)
Es sei k ein Kreis. Die Gerade s, die mit k zwei Punkte A und B gemeinsam hat, heißt Sekante bezüglich k.
--*osterhase* 17:26, 14. Jul. 2012 (CEST)
Es sei k ein Kreis und A, B zwei Punkte auf k mit A ist ungleich B. Die Gerade s, die durch die Punkte A und B geht, heißt Sekante bezüglich k.--*osterhase* 17:26, 14. Jul. 2012 (CEST)
Es sei s eine Gerade und k ein Kreis in ein und derselben Ebene. Wenn gilt: 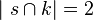 , dann ist die Gerade s eine Sekante bzgl. des Kreises k.--Tchu Tcha Tcha 18:23, 14. Jul. 2012 (CEST)
, dann ist die Gerade s eine Sekante bzgl. des Kreises k.--Tchu Tcha Tcha 18:23, 14. Jul. 2012 (CEST)
Es sei K ein Kreis und s eine Gerade. Kreis K und Gerade s gehören ein und der selben Ebene E an. Wenn die Gerade s den Kreis K in zwei beliebigen Punkten A,B schneidet, die nicht identisch sind, dann ist die Gerade s eine Sekante des Kreises K. --LuLu7410 18:58, 14. Jul. 2012 (CEST)
Wenn eine Gerade den Kreis zweimal schneidet, so liegt diese Gerade automatisch in der Ebene, das muss nicht nochmal extra erwähnt werden, oder? Das war doch nur bei der einen speziellen Definition mit dem Radius!
--Monsta 20:43, 17. Jul. 2012 (CEST)

