Lösung von Testaufgabe 2.4 SS12: Unterschied zwischen den Versionen
Thommy (Diskussion | Beiträge) |
|||
| (7 dazwischenliegende Versionen von 4 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
'''Lösungsversuch Nummero6/Tchu Tcha Tcha:'''<br /> | '''Lösungsversuch Nummero6/Tchu Tcha Tcha:'''<br /> | ||
| − | + | '''Voraussetzung:''' Kreis k mit Durchmesser <math>\overline{AB}</math> <br /> | |
<math>C \in Innere (k)</math><br /> | <math>C \in Innere (k)</math><br /> | ||
| − | + | '''Behauptung:''' <math>\left|\gamma \right| \neq 90</math><br /> | |
| − | Annahme: <math>\left|\gamma \right| = 90</math><br /> | + | '''Annahme:''' <math>\left|\gamma \right| = 90</math><br /> |
[[Datei:Test 2.4.png]] | [[Datei:Test 2.4.png]] | ||
| Zeile 19: | Zeile 19: | ||
q.e.d.<br /> | q.e.d.<br /> | ||
--[[Benutzer:Nummero6|Tchu Tcha Tcha]] 19:06, 14. Jul. 2012 (CEST) | --[[Benutzer:Nummero6|Tchu Tcha Tcha]] 19:06, 14. Jul. 2012 (CEST) | ||
| + | |||
| + | |||
| + | |||
| + | Vor. Kreis k mit Durchmesser AB, Punkt C im Inneren von k<br /> | ||
| + | Beh. <math>\left|\gamma \right| \neq 90</math><br /> | ||
| + | Annahme: <math>\left|\gamma \right| = 90</math><br /> | ||
| + | |||
| + | 1. Punkt C im Inneren von k / Vor.<br /> | ||
| + | 2. Es existiert ein Schnittpunkt C' von AC+ auf k / 1.<br /> | ||
| + | 3. < AC'B wäre somit = 90 / 2. , Satz des Thales<br /> | ||
| + | 4. < ACB = 90 / Annahme<br /> | ||
| + | 5. < ACB somit Außenwinekl von Dreieck ACB und < AC'B ein nichtanliegender Innenwinkel von Dreieck ACB / 2. Def. Innenwinkel, Def. Außenwinkel<br /> | ||
| + | 6. Wiederspurch zum schwachen Außenwinkelsatz, da Innenwinkel < AC'B genauso groß wie der Außenwinkel <ACB wäre. / 3., 4., 5.<br /> | ||
| + | 7. Die Annahme ist zu verwerfen und die Behauptung stimmt.<br /> | ||
| + | --[[Benutzer:Mahe84|Mahe84]] 20:04, 14. Jul. 2012 (CEST) | ||
| + | |||
| + | Darf ich mich auf die Innenwinkelsumme berufen? --[[Benutzer:LuLu7410|LuLu7410]] 12:14, 15. Jul. 2012 (CEST)<br /><br /> | ||
| + | |||
| + | Vor: AB=d des Kreises k, CeInneres des Kreises<br /> | ||
| + | Beh: y nicht gerade<br /> | ||
| + | Ann.: CeIK und y=90<br /> | ||
| + | Bew.:<br /> | ||
| + | 1) AC+ hat noch einen weiteren Schnittpunkt mit dem Kreis C' I wegen, weil halt?<br /> | ||
| + | 2) von B aus kann es nur ein Lot auf dem Strahl AB+ geben, dieser liegt laut Satz des Thales aber schon bei C' I Existens und Eindeutigkeit des Lotes, Satz des Thales, 1)<br /><br /> | ||
| + | 3) Widerspruch zur Annahme | ||
| + | q.e.d.<br />--[[Benutzer:Monsta|Monsta]] 21:07, 17. Jul. 2012 (CEST)<br /><br /> | ||
| + | |||
| + | Muss dieser Beweis per Widerspruch geführt werden? Ist meine Variante auch möglich? Was ist in der Aufgabenstellung mit "Beweisen mit einer Umkehrung gemeint?"<br /><br /> | ||
| + | |||
| + | '''Voraussetzung:''' Kreis k mit Durchmesser <math>\overline{AB}</math> <br /> | ||
| + | <math>C \in Innere (k)</math><br /> | ||
| + | '''Behauptung:''' <math>\left|\gamma \right| \neq 90</math><br /> | ||
| + | |||
| + | (1) <math>\exists C': C'\in k \ \wedge C'\in \ AC^{+}</math> <br /> | ||
| + | (2) <math>|\angle AC'B| =90</math>° wegen Satz des Thales und (1)<br /> | ||
| + | (3) <math>\gamma</math> ist Außenwinkel von <math>\overline{ABC'}</math> wegen Def. Außenwinkel<br /> | ||
| + | (4) <math>\gamma \g 90</math>° wegen schwacher Außenwinkelsatz <br /> | ||
| + | --[[Benutzer:Thommy|Thommy]] 15:45, 22. Jul. 2012 (CEST) | ||
Aktuelle Version vom 22. Juli 2012, 14:45 Uhr
Lösungsversuch Nummero6/Tchu Tcha Tcha:
Voraussetzung: Kreis k mit Durchmesser 
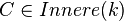
Behauptung: 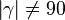
Annahme: 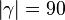
(1) 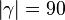 // Annahme
// Annahme
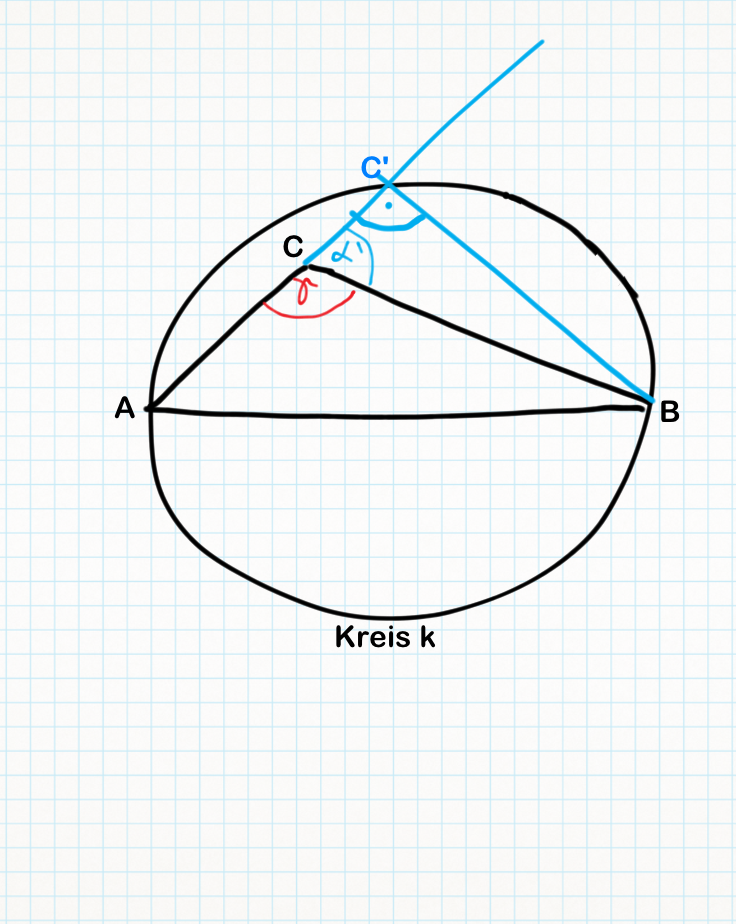
(2) 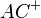 muss den Kreis k in einem weiteren Punkt C' (oBdA) schneiden, da nach Voraussetzung C im Inneren von k liegt und
muss den Kreis k in einem weiteren Punkt C' (oBdA) schneiden, da nach Voraussetzung C im Inneren von k liegt und 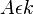 (Durchmesser)
(Durchmesser)
(3) 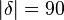 // Vor., (2), Satz des Thales
// Vor., (2), Satz des Thales
(4) 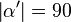 // (1), Def. NW, Def. suppl., Supplementaxiom, Def. rechter Winkel
// (1), Def. NW, Def. suppl., Supplementaxiom, Def. rechter Winkel
(5) Widerspruch (zum Korollar 1) im Dreieck 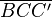 // (2),(3),Korollar 1 (mindestens 2 Innenwinkel sind spitz)
// (2),(3),Korollar 1 (mindestens 2 Innenwinkel sind spitz)
(6) 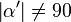 // (5)
// (5)
(7) 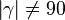 // (6), Def.NW, Def. suppl.,Supplementaxiom, Rechnen in R
// (6), Def.NW, Def. suppl.,Supplementaxiom, Rechnen in R
(8) Widerspruch zur Annahme // (7)
(9) Behauptung stimmt // (8)
q.e.d.
--Tchu Tcha Tcha 19:06, 14. Jul. 2012 (CEST)
Vor. Kreis k mit Durchmesser AB, Punkt C im Inneren von k
Beh. 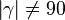
Annahme: 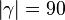
1. Punkt C im Inneren von k / Vor.
2. Es existiert ein Schnittpunkt C' von AC+ auf k / 1.
3. < AC'B wäre somit = 90 / 2. , Satz des Thales
4. < ACB = 90 / Annahme
5. < ACB somit Außenwinekl von Dreieck ACB und < AC'B ein nichtanliegender Innenwinkel von Dreieck ACB / 2. Def. Innenwinkel, Def. Außenwinkel
6. Wiederspurch zum schwachen Außenwinkelsatz, da Innenwinkel < AC'B genauso groß wie der Außenwinkel <ACB wäre. / 3., 4., 5.
7. Die Annahme ist zu verwerfen und die Behauptung stimmt.
--Mahe84 20:04, 14. Jul. 2012 (CEST)
Darf ich mich auf die Innenwinkelsumme berufen? --LuLu7410 12:14, 15. Jul. 2012 (CEST)
Vor: AB=d des Kreises k, CeInneres des Kreises
Beh: y nicht gerade
Ann.: CeIK und y=90
Bew.:
1) AC+ hat noch einen weiteren Schnittpunkt mit dem Kreis C' I wegen, weil halt?
2) von B aus kann es nur ein Lot auf dem Strahl AB+ geben, dieser liegt laut Satz des Thales aber schon bei C' I Existens und Eindeutigkeit des Lotes, Satz des Thales, 1)
3) Widerspruch zur Annahme
q.e.d.
--Monsta 21:07, 17. Jul. 2012 (CEST)
Muss dieser Beweis per Widerspruch geführt werden? Ist meine Variante auch möglich? Was ist in der Aufgabenstellung mit "Beweisen mit einer Umkehrung gemeint?"
Voraussetzung: Kreis k mit Durchmesser 
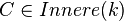
Behauptung: 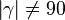
(1) 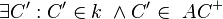
(2) 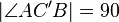 ° wegen Satz des Thales und (1)
° wegen Satz des Thales und (1)
(3)  ist Außenwinkel von
ist Außenwinkel von 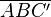 wegen Def. Außenwinkel
wegen Def. Außenwinkel
(4) Fehler beim Parsen(Unbekannte Funktion „\g“): \gamma \g 90
° wegen schwacher Außenwinkelsatz
--Thommy 15:45, 22. Jul. 2012 (CEST)