Benutzer:Schnirch: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(→Beispiel für das Einbinden einer GeoGebra-Applikation) |
|||
| (22 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
Die '''Kukulkan-Pyramide''' in Chichén Itzá (Mexiko). Erbaut von den Mayas. Wer so was bauen kann, muss sich in Geometrie auskennen!<br /><br /> | Die '''Kukulkan-Pyramide''' in Chichén Itzá (Mexiko). Erbaut von den Mayas. Wer so was bauen kann, muss sich in Geometrie auskennen!<br /><br /> | ||
[[Bild:Kukulkan_Pyramide.jpg]]<br /> | [[Bild:Kukulkan_Pyramide.jpg]]<br /> | ||
| + | Volumen ''V'' einer Pyramide der Höhe ''h'' und der Schnittfläche <math>f(x)</math> einer Ebene ''F'', die parallel zur Grundfläche ''A'' der Pyramide im Abstand ''x'' zur Spitze der Pyramide steht: <math>V=\int_{0}^{h} f (x)\,dx</math> <br /> | ||
| + | Da die Schnittfläche <math>f(x)</math> an der Stelle x durch eine zentrische Streckung der Grundfläche ''A'' mit dem Faktor <math>\frac{x}{h}</math> entsteht, ist also <math>f(x) =\left( \frac{x}{h}\right) ^{2}\cdot A</math> und damit:<br /><math>V=\frac{A}{h^{2}}\int_{0}^{h} x^{2}\,dx= \frac{A}{h^{2}}\cdot\frac{1}{3}h^{3}=\frac{1}{3}A\cdot h </math>. (Keine Angst, dies ist kein Bestandteil der Veranstaltung sondern einfach nur eine gute Übung mit dem Formeleditor--[[Benutzer:Schnirch|Schnirch]] 12:13, 10. Okt. 2011 (CEST))<br /><br /> | ||
| + | |||
| + | ===Beispiel für das Einbinden einer GeoGebra-Applikation=== | ||
| + | *Die Quelldatei gibt es hier: http://www.ph-heidelberg.de/wp/schnirch/GeoGebra/Spiegel.ggb<br /> | ||
| + | *[[Hilfe:Inhaltsverzeichnis|Hilfe]] für das Einbinden einer GeoGebra-Applikation<br /><br /><br /> | ||
| + | |||
| + | <ggb_applet width="581" height="520" version="4.0" ggbBase64="UEsDBBQACAAIAIpVe0EAAAAAAAAAAAAAAAA/AAAANWViZmUwZDYxOWNlNGZjMzFiYmVhNTcwMDIwMTVmNzdcUGFyaXNpZW5zZV8tX01hbnVlbF9GZWxpdTEuanBnnZdXUBPg0+4TAoQaeg81EaQKoYbeq/QmvYTepHeQoigYQhNQDCDSpYNUQekBlCJVEZAeuiAdQT7/35xycy7OOc9e7u477292dmaf22+3ywBqXU0dTQCQAAAA/gvA7Q+AGoCEmBhMTEQCBoNJSUnIKOgpKcjJKVho6ajo2Vk5OdhZoVAuuAgfF48QDAq9K80vJComISHByYdUkEHIi4hLIP7zCJCUlJSCnIKZkpIZwQ3lRvw/67YbQEMCFAL4gYA8AAIaIIgGeNsP4Pz3TyLgfwvwPwQkABESEYNJSMnI/xU0UwMIgCAQASGIiIiQ8F825l8eQEhDRMstpkJMZ+wE5gmgR8RnFJHAVBt6GEy+HsLFnQMTSMkYmZhZWO/w8t3lF5CQlJKWQcqqqWtoamnr6JqamVtYPrCyRrm4url7eHoFBYeEhoVHRCY+fpL09FlySmbWi+yc3Jev8t4Wl5SWlVdUvmtset/c0trW3tHb1z8wiBsaHpmcmp6Znfv2fX5ldW19YxO/tb1z9Pv45PTs/OLy6j9cQAAI+D/1f+Si+cdFQEgIIgT/hwtIEPafAhpCIm4xYloVY7BTAB0PIp6EXjWjqKGHFCZucsjgHPiVjBEusXLn6D9o/032fweW8P9F9r/A/jfXPIACBPw3PBANQAlweimC34sKU9j+5IXdh/9GDu3rcyVADPGmPKnldbCiXyZGpwXmMPx4UNbofcwexAHOQVVqKaBoRMXlVqZKcIRrkZsgHIYB0emxbQMaYTHs2U2GERIBqsWbmRZkxUfylsJHIFzoEsmE4mQvslkwsWVycXxJ3vU1Z69St+XY3FXu81iYV7ftZ8k9bKNquY8xleuWYlk8p9quouKkRL5AVFXUH7b2Ylsc6wIXrcsaC8tfuypazufzLg3J0Y0pAHdKIdduxRSqLzEfLFMWLmTP+ybY8t3mCWVuJptooX9QCTHJ1Xo/Lg5YUFJi3GmJG6nt15XfJBWbvnZaley+K9efFsYHKnqcA3ZP1YZwk62ZJn2AWuVBMMqB1UO2n9WgRKRkSnFiOyFOd2ioOzEDc7o3Lz2oIG7ysMnWM1cqTKhES8a/X4pqdGj/l253lHIo9GAsBkm/kfFMSRrWWhqBnv+FlshpStfzrP4+flcryG0Y7hF0nMVh/gloIcmZLGUPPXKaOn0F11fcWULW1FogLMRzINCQXcyrAZAXrii5Nd0cQ7Vi8TWercubuM+8cbrGAm/4IWmT4ButGpcrHwahlO1ng+2nJLmPIyFFcj69bxbPBHBEnxdpjWahORb5u6UONLWaQdQiD+IiyYxkejYL0dAziZd9kL7ZdA7UUWJ3bsGdqTczEoeuXfWp2TXDtwArpqU7MbjyyN+cTyM3cpOuTdjMW9BqomKde+0eXT17VJFXXQgHPhhzdy1b/yOKTvF3izWX9dpuJqPwAMoqaXB9N1gB1yW6G/R6NmSfbDH48l4t5WmV7n19v6HdEJaRjQ/8nPG785XhubqF5s0tH9vihUvvCJsMqZOhT1xgFU5psYLjnYZl4ZGfLX6fOAVzw11do18WXmQ/tadiiJB3eve+pU6qUk7HC/Ck5JmMwXeHvk/WoXvScgfBf1kPQ7N9Zftqty3EbMfGhIUPwkhL2DDM2H1biNhS0dGjJIlRkSj1J7Sk30GEfNFOnyk4IrrZMIrZhA507s2Ett18WDTpiCNnHcuNd870tZpiU6zIgZ8zoajAR1Mi9phjjcfzLU+LvefOxPTLdlDmUkfWyqVv47J14raz1xIv5tIuco3TTKbndwTbD2i6BTIT5ItuvmJPyhc/n7WihP+MFqSYxd+EM1StcBLYhePMbWz4xWiDAqRzQlU7T/kqFeLezpIabBQ+yStMru5UbpmnD7S1Gft8VhX4JMtP02FClP0WQHY1uODMBdbdlOdfoZTuiQxonErP9aeYartcV5qIsjSl7nXGvBX7jOBo55wsVYvvYVHQt3yRuhg5mUCQNQelMGFBwhN/FvADFdiQ7Dtc+Ky03gJOeUxfqxcA63hoA0a7ZWo7Z+t2JJTgPSteTVewQ5TB7ZWk5OnIceOlOMXIi6yV3Xy+gVZpE1WN/KmHrflaYPn0mJ4bwcyCScFQYaH7aO3LYYDltOxm9sO6rVZr1xGCpkqSfgLjht/1V6zL8grL+S1vdv9qfCHblOEQQYNDfVwwvfkDqOdHP5/USMQozocP96e8IbIlIMDEls+3+zIps3al7i8ICta8cNYkRHEV4n8e10XN7Wcq8Kwymd55lhr3WJP8DTuuVmwicg67xfpuy4K12tQz0LBMKN5uGqCidA95pnCXzQJ5CyAM15wasLTsXV/QoDeuSEaBENr9T8aCcMQfkw7Ln+513ivClT2onP8kgenbzBi3UFqxdzhMmKmV7LIxarXUY852SmarhGeNt3GOdb1g73dcxnRVivEoB22JqjBXJU/VuCeM9CdocWVYAuHQW0DBey436ONf8OBhdv7u60QoBns1BWVke7HOsYnFUrinmSoPfPMH7KoSkCLxlewaSEzAdgH/UMD4o11lEvoDcL3EmauRS5iZOWETXRy4SzA7iU4ITStB9Cp5GZi37l6wZpEj+L3m+Y/2gVJsJ5eBUhTXgaFjOGgp3vZDlbfvTaFEi4sQr5TYyDVL915BXNqqYqd5DcxqSnKfV+411+BMOje6Vr4JN6RVsW1vvtalZqmvLNYWhPLvFqDL1rINPqkuBNsu8rYH+BLtqhHtf3jlTKGSjl4HTUPPoWuSFgzjttOrXY1JVm+fLX7nEUfg/jYAzmTGlGSPOamtt63PsHOR91tNPwsVn/vD6H0ga5zhloaMJR3Z8a0NHQXkKjSp0+3mXOxtvgu/gb/GvNl5H1L91MyZ6npB+Sr6uXMPRLawgr3pwtjpmCP+8IemL1uP1NfPNBjP9Yh1C7tqUhmWXxNkO4bw5eXggUBWh5Rfr41bMZtLyPc/nt0CQkLYMlcaMnBHBMi1vL0JHE91xscTRxKuQy8fMXqOxzeUdo+jPz0xHR4CBN8IrMvf5ZjmFmcYRERSeXkg8QQFl4SY79deoiRbiu8p0qEtJGuc1oF+VOjoT7N5b9JeBkZO3XsYO4AS7lH9w7RhuxYUyrKftRQnftriPZxlaCsh8DGkexG99sKwH31D5GL/c1QxZY6WSQ3+lIuCwRhD5PVAC7FIF5ji56omNBBhhweBvkGUyIqri55ruDoC4S1UTsOrCYYKF88rqg+3jVR+VwnqbmlCrlfbNHK8PZ0LmPjhBlZkh+BbQG3HPbY2O90RyTWxSuh6UB5+NdhD3e9NZt+Pueu/DM5yz2M05WZT9lEq3mSXR1owapfcg/XTZQ6BSQdt7gebGhZoRnigtEuL+MloxN7UgidC8MfQkvUyw45UYR3Llvfb9q7W9gatdgexdc2YooYk9geotu37WlpF4fnC1fsnw755EbzkZ75YQiesdDSV7mmXyExNjUpGo2tfNnjd5NGH01179vJvhuwvp/GC3hReSUwF910SyOK3M5Wsz3e9X3x6n7QJe7mR6mLLaZz3CgJLJyA7B9dYo1F1tmYkAOeYnZHpt6/QRucyCuL6roDg3W6Jc7lGLfhJGeNSSVD3rvIAAOt+UpqNEpUuAGnU55ogyCYrLzVjRAXv9TO9ZRex8cftS2tPqDDv6BDSnQDWJ4gfPT4QwTcYNlO9ovaBdboTBZ1ATa/vH8zSvghmM1uDKaQalhHFVXM54qhtIU85/757ap1cW+3HACHVZAE1K5Z0pREe2VcJD4xiv7yhjUM9hLHgFE9zS5jo9CVSPlqvqLb6K12dRg2Q1O+m9/FENzCSlcs4ynCOvKV9/Ft1+UAOWxB3PHeZ16hn8qwsLpmcEclV8PgWwHRhngr5PS/I4jvail0RPWA6oEhHKiC0q8/bkmdeYPNL7oLqrE8LH9tDWwp7I58s9sNirsuUxHL5nFHM++hJlMaHRwCvyPc0Ig2SWMav9RmOrWgslObnj5QTGxuXxsakeQYCmRd3gaHoGAEXZplBrSA1lMeaoNHiSH3FQG75R4H5WAWBxwaIN3XR5hdDAyQsGGLxwkhlYp1S45wtiAL/TvwzZi66LOUe6oNuFpktwezZWt/aTsPy79/0Ka4yq5KLx1ag8rQGSNM2YbdonSP5HOPaJ078GM81qgABKVaZMf/ixfZrxeYNi73ZxpKJoSPtch4NGaeLaWTJXvBkb0fGZldaBLfTpwfDwC/qFacsFZJUirzumBUeUEb2MENfuM2AdUFRlZZrVBA+i00I8fKwrzga9wmUcvBrLU8d5ZfBCONe39A3CZvuLZUGj4yDjjzbcgf1JD+TQrnksqWqRDnyq1jNvT+UtTazqKROArEF3u44hOG9ZNeWnB0k652NVcDdMdJtq/noI2sYgpurUOijP51Mz3WVGq+ltsE2kIhB2wK5QsVwapFdbuMpq5Gfn04wz5xthEGLzR3tOiC80nF+53p0g4xBLyeg+ZdQy6k8u4aGiT1h9ufvGb8OPvitQwYs5e7vysImDoqrIHFOmGbGm27gNJrVxEoTDD0yMXrFfSEfG1Lkey52MUNk0g8FYvQ9BjKYmYtIX31jewnJF5Trl90vT5J4Oi3yjZZE+y2YWAvZewuw/goghocq3Hj3fRT2yvSyF7KhXbd58G7wnayfI8vr3SHOJ7x7niRBcsy5rVk7YVM/7T7+eZ1MPvS9e/zNGSit92WsuT0QxnxS4UMuLwCHBR7+tM4z0lzWPlltL8A3E74IlugUxUj+4YfN6xR+drSBADW399FzFbuydbkdvRIAnLOfO9fvLtX4AwPDFfuwZX1FvU80JfE9jDuTDWMklwZiF3PehCCjuZB6oNCs/yBzgVj90dWchkLaPZajAqVVX0bP998ko+4QM/6EPkX61ClVjEbW1P2jovJmjc2q0M6cT0RRh+/XJ2hysff/Dgx6oMmnSNiV8MAK3twJUeMHea4d1Z6vbNZKcpLazLd/OeOy0dbBvxF49Asba+6zLuTJQXI4+1xWz7Ok+879xlERF/8IvHDez6G/3MP4FGVln1NmrhgPJKwcuUPJk/SIBqeyPV/+bz+wwQOqb+724GEwcEqAvzLRM1DFG3AmNUEkh9d+Z8rReozAi3BHWcdY81BagjWex7zOO5YTnrIxozdf+xmPXnFOx//4Z2vGrFP7O0pnBosQifLHLK90hobha1uylp3hf7nDllPtFUr2n37pXr8ukT6pI47P0SbLHuJaThnxOejVkFvwy5eJIOvYzwgPUYhtfnuUWYKvXGMnrZa28MxBwn8foJQ6sEedkazt3hVN92dbQS7P03LlOUvd5kxbstW7vnNkHU4iXLpeJmi7psl09+xe7jNELoU1HG305hDBMTJD40hkz41Abp9eUkQzM4Q8JwWVdkE9/rvmc43M6FobLwv5Olg+uqTy3yweGq7Id1oeWUmnWoitxKi4qAYxqkEge2hL6cOyfVPzmer7KWlw46FktLuf2dpcc/CSmNCV5iQCre16oKnMWROhMNExKXlXklyH4h5ZIkViQjVyPSpxamH2GV7hZmO+m+7CiNmP2W8xyOzkz8D0yWe9k0G+ZJd/3jNd/MKtzDgHJANYLQkTukuY4B/7/oMyuyi4i4fqxfKf1RL1Je0Ff7moCdHLFyilJ9atJpXHQMyMVX0+FXKNIZBW9/ddOoRbiuDLjdaXfhhzsY6rxH+3KN5O734MuW3XpNsC5ftS47QjPnOlZwMxbIO/w3ft7Y70elm7NqtDbkR+7BvVND5/DAGJfPkNDkjTTRYsfvvEQMcrYvqsSt6LlPCcfVfkYN7FSHRy8FNi0ZmkM6U9Ab32l6cL/oLK+tCFYn5ClL9kTsUvLwYL9I4iZGdP8s8HvacQ/Up+7pV6ZijHzPw2E5OL9ZI2R5Dw9Ecn4RFiPgCVsthAxPhjfEvjUXbqF4yzJorGUVTRFVbocwvQ3Wumoh5fURDlmizNpvdD0D0BF9wCHPA2KlsRF890DL7sNQuqxZA8i+tej1+YI6+5ePhH90bC28q4Tr7e1ei7TfB2143MMqTkj4V7SiyP99H22xhFkmruF9G1BpeGBjFMW+JWDiSSf0qPsmdKDqYoDXgjXNIPgnhc48c/8dSeiW4oVOnU2/FpNE1ZaL7ydXyg1tbjKBDEJX+jLzFWARQB/LtUK1pzTFu/DG8/LiEaWqhYK7cNZZDJ8srCaIMZsHcEAlG58DigzGo5Ldp9pBuWWCCmXPuAtljsMklnG5vX7qWXQOX12cJlXaAOOSbDUIq6+3tstb8gUAPglsuWvCM+XMXdR1szkm6WZmyWRnkeNZO/9qWbGdRFUbx5C6C5iAk2pFna/s1rgSRNu2kbF7yyQHnam7II84qlA8cUTZRYTwzRZQxzwWvEsA9/5Fhe1qrcT/2ECbK3gY0GPdx0sN0nE6Wu45uKTxmuEu8Qf546P23FsU7BtmVLMxFS8wmyMF7t3SLrVlfhYG8t8Urb+UXLAwLLRJwXfj8Yl5+oLcXHl5GYMjl5p3EqhMWv1ufvFFSwX1ONGQnO7yuM5d96L77hN+mxG/0I5TFv28oYJswzuIzAC1QbKkdCg9ckx6PFQ9Jw8+E+0avqtliKFz7mn1h25qTzRHLvfCF/KNztSXhX6l3fV9GupmOOCHnW0sNNZgfcldoobz9tjulUEBH8nmJzmGjm9BV9pTIwY44jEWrKsgq+cenHDIwReckbj0CMaOU4Zgxc0CgviixcqThPhz6hkGrTxljE8PC1l2UX/3tNZPfu8C9jXcik3l3QRMDlDJ2sevc7fj5QxDIrYE7H5UXloEEQTnfqffZzR9kGwHpkcG3AnQhiwpfg2q8pP6eyUU8J6fa3lanb5OK3FARcCaEZWGwMP8b/OhAoU0m/0bDAqsHBchQYsXqEjXvz4j1NNReERllpOu/4T0hYm8X3s1cIRNAT63NOdOghJcGIYTavNBHDU4hZlfthHWJqT3g/JffyUOWbDBimhD+qLtkL+1q2c2fdMkGI+vErKMAG5DFePrVrzqpwPvc1hyqBDhZnIOiZKcOStBGEZfzni69mUj3MvMOi2ojVcMsCdLLl5DJvx+rk5wdKF0cnbwElrfCC560yxluA1fbXbj9ZHmPpjmEQEsmZimefJeDpdqQAFPg6ZR3ggQkYaeB5jynn5ZGvFY7k1LwgH/Bc5SQtyRWxvhoi8cuqogVTncBOR32HQ8kBz6TF1r4grxscFC8s+xHhqP7ZvDy6M0+SlG1gt8e4w+eKK8tJOhWgPVPg/siyv7f6QYCBlFsAlYgeo8wa85rEVxLTL3xKB7ReU7QvaXr7D2OUalRgDc6KQ2OaEXweZconqeb1Zok45kFv9/upDJ8jrEZOr6sg/CScnc001wvOtnk/JheGqj+zoZgvxyUAmOIAgGMiNi+dWwjHzDVtsN6qoBl0ZbK4OIDyllxHM8qkf2DcArCUWK060IYgJR9CdTw+FLAjNTq9yuHtPQ9xfJyHrP2JQRUyCzgsPm+cKXDRTi8IRgeflED3r2f2F+5aCj+IC9RiZv6Vh88pb3qakqL9Mm4Px9KzxpCUovmBfwsCkQ2Kt5nUpYMDlOXPRp3FHPZTux0Z6N/auXT9NBnYprb9oX8N389asJQTSHuvSzok4h+jUptoxP2G5WS8TOxBUFztdWI6Ffu75UBnixIy8vlOl/XK7X0H1WjZuSn7Q9ei7Pj2Rk631zD4/uDURa0SzEEh8TkGi5hzOuzrpyy6GJTTYWOMjKfWLjnkvGA7Xjuq4fEfteM45WYmplc7CH93rBfQCuRigeLLBHWm9+C+4Hp5Mlxbmyk/0fUkhGywncEN3ruR7V9HRoN2QnhbaucXhntise53pGa5LH/E0TKcKmj4eGT2LjkmvxpBiwscFeqGEji/fvkE+dlS/Ej28NsF7R4McC6STmVCOnwDrM2G/oKBCfOObwHo1oabNN2pbl7NjHJo9AdlwctjY+HUba08Tw5937Ymf1IkiF3O/Ieqer90G3uDeY22FssdM/eMYQbn79l+AZniY/pBTXPlpc8DUyvYoPjaSAuzr85/+cWwlWOKzeWB+BEjCCnXOkSleo6rk+97vILC3eQQE5fzu/IJF2DAzcpcqeNI4UfQjHdJu7LPBR4sI2+p4F8i737zVuBt0CqPRQGiFBoCIjTRraH/OsrCPf1UVTYByeDs0fMclpWXbCtvTDcdMGA3htTwieF+4yW8eo/yu5eHMforCCYOBUOlOa1bZlMTojcFM7VVmh+VRnzqpaK+pPkZHqll7ru5SYADYEBU649kf4mIzOuwwxI8n+1I7Rtb1xjoCIqJUBgdTgL60Cg+yUeqnzJtklFp4Wb2hdmo0Q1cYshdighR9cCfyTVKVLplq6oZJLmewMgwBvXXT0T3p1iW5zKi7fLdjjgKfUiFiSqFSJb9nB+VRpEYbxaED2/b06z9yO08OivrXle1IFp7Y845nTcSxR7useQuT6MOT+uEBE2gUvSU9VeGmedJ9ge9JpRHgDDCQKoVI43HHbYAhC72vFokssbq7Ua/YbPOFlDmQHbGUrm+G0eYYKAk0O7fg1rskRmUy6viJmC475jEBblO1GFC9HdLEBKtMa9bsC+oaxa7L/qHobLyvuswzGH3BbGQrl3ek0ZNA6Vn0Bn1kea8timfcVKuAHTKqBn/psYUBYTK+vvjJlWIP8l1FeKMN2kDPhYGIB0wQb4bsNIhwhRLPa+z2glg5FB/148h5exXoslw0JBotO/OspYdcBcg1tFZGCsvI4peCWPc8rdKAggAlgtvARbe0x9Zdo/twiPtBHzH7yQTSG7d98XGasHSjK17sAzFbiEI5SrBmHxi8D2hzpZH415TEzmCETZj6SJmy01E4zB5c9LlDoyS1GqAJ4REQzDB8A/s6rTKWrKMZV1sn6KYUmwed1hDYdCNKJb7SFAnFLlMMTd6Li38qMrePlPP1uC3CxoqTiv4s3m3qTw8yuwDnYQ+5YfGDnT6N7lHtpbjxrQj/S12TVk/JZ+YTvYI2/ClZ6uCAdA4DbNBvAU0IzHRdOGYNf9bdIGC193eXOMd4oCplKFfOWfCtiA4IZoijtir9DP9kwfo9BEDudn8HkEv+uC/HIK8W4ytd5U6DCW4py3UG2jr70ET0X/MBQ+tF9P8ETE7o52v9/uCxyCAsX/dy1AMCYx+dlM8dvtOESU14TLDWIB5iPrNt4AZA61ddVpnBjw6rKSdO/sDQaS7vHkIIqe+QSEn7d1OQKJT+bi/qt8C9ZNbwEcMeJkyZIn66z15pYrPUTEM1a1fGBxbj8NIxu1GMQhZ55ZgSjera6ZyoJj2MroX/3BRMJsQ1cXyz6IClBuXi16sWlERFnQplnNaL4nqmY5WGg//KKqkn+oa7pjmDP5igAsdcjhXrrnhVc/ANopTdjL50P2yda2IpylzhqXSi+sJroDr+XKu5kyLvVj9n9kmi2zqqPSpAZ1+tI0aZ0St3hlK7JFN5+Pw1MYZHAj2+cZT6Pigs3rGBGdjBRfiyz3nY5cpZ7669ey8K79qjsi04ZVO/fEgvRwKBTyqCZpeOBUNOPfTCGV5O4R0ZQEpvCNxschXdjRWPUZDWT9uMQT1gJGgTCLUu5eScDQHObUCGZbGCNOBGRV320vjY/nT6YfTHctiE28FEaLqauydOnjKK2VA2+a2PhZDY+IZ2yYZQWGCnuts0XQJCAWxlJQL9mrQ4yH5vEr+l/JP2H1XKAzWhked9AVHBd1U/66fMlSjQv3N6j5z2LBJGXmxNq9+254gXR8U7bx7ldV97R36CLg79O5OR4NqOBkcfgu4N9t+wzYQWfDU76xe4p4fjpefDqbYzqxUE2wdlub30K9mX2SvWGxoxW4tPYl8d7zcekYDiqiSnp7/+v7PIu+QVfO0NEguOyEdNszWUAARw+Z9wNtYpclzKmQnXfpJy4yF87F3te1a6C9lbwo3LvT3F9CU0DLdAhS89I+GZQcolHVFzQjY6yGKRjKc+R6oQGPPh3eG8vCuG73xSdmqg4Uq+3ZPn4IkaqkryEqiE+OHVhuEgsmLaSh96QlUrTovGQp3cUE9tVVqUxzfOjoHLQAJ3+ejQk+KVQ4CHWijxWp2r5rzz5K+MqbA6HDw1yRIPtilZYH9hfdAntR3kT2GiRZxwp5nkifkPyT81oP5ZN5ZF7yGVJaPugZyDr/SbYL5Op0oNmeluB3VyGy9Ol6efhOuLP5GPpNqROUAEiNQ0jqrqZ4hQgwAJBBr6Z7ofUrImaNlapkZqQQnO+H+Jg64LkaTT2dy+UoKRnwDZWQ+vkGIme7NBbmjsxahUbv+dx0z6bIyvpFV8Xag2TIDdQZlatgdVgYbSsSOi9qcMlWoc0zTQoZqQ2NEwhfNNAN/dpMOyUeZnmkno3iHRA6Wti+HVPKrCog0fAEFIZoZxobwrAQwg6DVGFrNxoAELzNGtWHyY95QiqQ5T4MPjk4IujCvwB7YzjcZ9Kkm6Ry66sUxyRmYQT6l+RWcVnE8RREfC79QB5DluHHFwtMmG011p2cI07da4+IzXi4c706EMISyKzm8MmK/MzI40J3JyPzwl/stoM6sWk1Wjn+/ZgJY3vuhERg0/ahbhae1WtJzf9BibEHTEglRpcIx9NWUP0smVIHfL8kRqzChYr9Enlcdde13iuLgnuKD0uy/krZkM7XPRkXvn7gciczSzFtbM3HRfvmucMk8FrHaQUn892rVitX7Gc/IuubwuH0ndi6lZr83CWH3o59FGTb2GVJQiJ/9oETm2/GnUnKN5LcLMACLPsXXCFKcgfUnG4TEC8AB5nhVsfgfdSrWqWSihGis0YRmH2FAymvIpiz3OgO3piGMQd7KNKEbhF03n3n/JMwpyjRnST74l0bCZtTgpPQVTgPGTFyxcPFQ+4OmZ7VTGDz6h+jPl5utJkuKbchRDhOAqNwk+5iOPHhlI7tUNhYvn/9bDHxaRbpCScBHkeejHOevoiBY+mAOJY1cy2OlPzl9A4kJ9kXAaXAeH+gx5LRUeHO/YDkGCpMRKTZ/JnmqsQ6mJ0DmUZ5+dGeaNQE+0yuWbLaZrSXzQY3zM8cSI+2RdxG7C4X4/Qem17KfWj3l21ZdM5Qpc5xlr47sD530i1Nccr46xdoX530MdVtNI245zGn3FcXIiL6DkBWxbE9sdqRyqk2/xRYvjL0pcpQ6WQ+Y79KdXeKXOlAOxTN4OTa82zcS39eSmfZ5dPv9vwBQSwcILFqIF9ggAABpIQAAUEsDBBQACAAIAIpVe0EAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiu5QIAUEsHCEXM3l0aAAAAGAAAAFBLAwQUAAgACACKVXtBAAAAAAAAAAAAAAAADAAAAGdlb2dlYnJhLnhtbN1aa2/bthr+3P0KQh/2qbZJ8SZ1doekq7Gi6VogPcNWHKCgJdphI0uaJCfOsB9/XpLy3Unr3JodoC4l8uVL8nnem6T0f55PM3Shq9oU+SAgXRwgnSdFavLJIJg1404U/Pzyh/5EFxM9qhQaF9VUNYOAWUmTDoKEMZqkMenolOgOG0dxR41HvMPSOOE0FZqqMEBoXpsXefGbmuq6VIk+Tc70VJ0UiWrcwmdNU77o9S4vL7uLpbpFNelNJqPuvE4DBNvM60HQXrwAdRuTLqkTDzEmvT/enXj1HZPXjcoTHSB7hJl5+cOz/qXJ0+ISXZq0ORsEPIoDdKbN5KyxN7DTnhUqAZBSJ4250DVMXbt1Z26mZeDEVG7Hn/krlC2PE6DUXJhUV4MAdymNOY+4pBGncRRHASoqo/OmlSXtmr2Ftv6F0Zderb1yK7IANUWRjZTViP75B4U4xOi5bYhvQmiE8EPY92Hqm9A3zDfcyzA/nXlR5mWYl2E0QBemNqNMD4KxympA0OTjCthb3tfNVabdftqO1enJczhTbf4GYYrBTDzk0I/xc/sT8GN2oLd5SLK2alPNDlx0sSSPyLcvGd7poHSxZrjvmCG/5pjihkX9ub/lnISvrQlLuX/ut7MivemY2yv6+7stKNijHLHfW7hKv/UOVJ9Z2dZ6Gj2trb/QGPHYmj1BHHxDSLByjkgMjQwReAMiHDEOtyRCwrYSUQkDDFEUIStHKHLOwSP4j0mnTCAOymyvBJ9EBBZiiFNEnE8xBJ6EnF+Cj4YUJDhHHCbZ5UloVVCBmIA7GiEGe7QuKQkIUpgI97B8iChB1E4mEoUCCauPMOvqIrJbB5UhEhgJYhWCV4NHe28G+QhRexrRwmXyctZsQJRM08VlU5RLLkAa4tEq6vn4tBEUn/UzNdIZ5IlTyyRCFyqzHuEWGhd5gxYkhr5vUqnyzCT1qW4amFWjL+pCnahGz4cgXS/WdrJJkdcfqqJ5VWSzaV4jlBQZXu65yMjadbjcNdzQtQG2PsDXBsTatdy7bgEjaFZrWL+o6oW4StM3VmIVGgDJ93l2dVxpdV4WZvMY/Z5LOX09SzKTGpX/DsZqV7G4oFUGIqsMxEi82EhRpadXNVgwmn/SVTEIOkSQroRojiFPwY9yoPXKjzGKu5EQISeMMxlzyDF1oqzzSdzlnMcUZnCbiGDkav+QIH5pfbFkSM316rCTyixtxV6/qY+LLF0Ou+O/UmUzq1ztALGxsoc6yieZdibioi0k5uR8VMxPvW1Qr+vjVQl32G9gNHGwIwgNIecg0LYj3zoZu7OlFHYy2EnghbGZdDlO4tBJuHbkWycF1uu31p6ULE5J8GIZU7uAhoPWbRbBytq+zfOz3DQni5vGJOftUYmf8NtsOtJLC9rUSe5LZ7+3ZWL9c13lOmstGricFbPaO+iasac6MVO49QMtJMrS9R/YgO9N9aTSi41nri7zgLlRvG6sO91O1bAqpm/yi49gC1sb6PcWu+zXSWVKa3JoBFngXK+sKjW1giSSrs+zLghHT2yyAHgaCw0456w5KypXekFMgdZ6XqanUGihxpmXs9AlzJ9cBWfxRMXoC4S1bR7WkAKBvcbmzFJl5ZmydV577Exd6WoDCKfwXZFuwwPouzOAl5dWgeW31Nqbht8zXJSg0HnURpwCxGs0Bye2dfgVhBHb/u0reF/C2tNaL9sIzL53iyqwHw+UA3c6VXmKcpeqPzjIVqlDQRCeH4EBt7jMmkXvn15RO/0r2P95S+xJ6MOBa+8b/7ugjx8E/RMIT1vgf4LzkhbtDfzVzfjbSLdEV+3C3xZ93275mN0e+RV+fAu/DuVLZcvY3EDVcA6PRrVLIE2bKtzFryZNtasYfer6K/dTah8wzbTMTGKabZhvss3hV8BZBfJHiQq3sUrWZZgKTJiA4oIwIluMI8xjyTDUCWEYx4w/gMm+ryAKT4pcZXuMd+iNd38AGR1gwKO7GzC+D/PtkC373UX+wW356wF7tIP10SHB+uhWDnGXUP1+PK514wF28Ibk+7gM61IsJAtlJGIKdbV8pBS7y9jbQxh7++iMPSonUjLGRRQKzmwwewBO3pmqKqotUt766KV2uflRlUX900EMtVO+O08rtOMujwWNI04ZiSL3KvR7oj28Du3h4WgP74D2vSX265Fm+9Nz9ABQn+qJ7d9v2Wt2vIF4cjPWdatzgWPyRJIzXj4ZwfM+xG4sIiolEb7s6YRg2tAfcUZILAkF036QXO2gzGyYe5M38Niu3XPr7tP4udalfQ3yPv9Yqby231m8zNpT/mGstnQ6bo92WE0PYzV9MqwyASxCZogFjkMR+azQ2c9yiCGDM0Y4jmTEOBc7L37+5SQPbyZZH0ayfiIkd2iXYyyB3BBLQiIc7ifZ12NUdmWEMSU8ikJbrP2/cezZHV4TnseHcTx+OhxTqK5FjCWNJGciFq879tPYnpDtee6wLol4CEkSyhGJZRT/a4leKt6iWl9X9RwfUu8c36rSsd/sJr4Z+ebuJJOIdCUDpiS13xlwW+sI0aWShjwEbin0+ljNuxtlEWX3WPhcB3h6HeCvDgH81eMCvno+9nExvCUb0nsbIbIbxSH4YgQVLofqcy8f4WPwoTwf4x0+fjmEj1+eugNAXQK1SxhHESOU278P+X4ukFznAq8Pgfz1k4V8YeUhdeBC5uCAMGSWh7DyTYjMVE1WEBybLA0dTGMDCjwrXI/GGqeCxIlm44SS0Ugr7j7zEj6W8r8fVGVqo/Naf+58fqfymc4+D3VmZqT7pZz4bZn8WCXnk6qYAdvbaapuVNW4t0wod18OXU4EoChkWQoWGEEGBiuMl++JoY7ClElBBReAIN18EL2n0oE8wCslvO+V0gY987KC8sAqaff8Uc8bmA8Dg+DHv2ZF89NpafREZxNdqVT7Lqdmk9oG5gWbSu4Mzp3eL6zR7L9MgR9AZAHTxlQQSdvCStjeSEC5TIlk68yu49Rb/8bq/pKh/aO8l/8DUEsHCMayNarMCAAAMSgAAFBLAQIUABQACAAIAIpVe0EsWogX2CAAAGkhAAA/AAAAAAAAAAAAAAAAAAAAAAA1ZWJmZTBkNjE5Y2U0ZmMzMWJiZWE1NzAwMjAxNWY3N1xQYXJpc2llbnNlXy1fTWFudWVsX0ZlbGl1MS5qcGdQSwECFAAUAAgACACKVXtBRczeXRoAAAAYAAAAFgAAAAAAAAAAAAAAAABFIQAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc1BLAQIUABQACAAIAIpVe0HGsjWqzAgAADEoAAAMAAAAAAAAAAAAAAAAAKMhAABnZW9nZWJyYS54bWxQSwUGAAAAAAMAAwDrAAAAqSoAAAAA" showResetIcon = "false" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "true" showToolBar = "true" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "false" /> | ||
| + | |||
| + | <br /> | ||
| + | Falls nichts angezeigt wird, können Sie mit folgendem Link [{{fullurl:{{PAGENAME}}|action=purge}} den Servercache leeren].<br /> | ||
| + | <ggb_applet id="gkykpjxy" width="1920" height="927" border="888888" /> | ||
Aktuelle Version vom 23. Januar 2023, 13:31 Uhr
Die Kukulkan-Pyramide in Chichén Itzá (Mexiko). Erbaut von den Mayas. Wer so was bauen kann, muss sich in Geometrie auskennen!

Volumen V einer Pyramide der Höhe h und der Schnittfläche 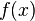 einer Ebene F, die parallel zur Grundfläche A der Pyramide im Abstand x zur Spitze der Pyramide steht:
einer Ebene F, die parallel zur Grundfläche A der Pyramide im Abstand x zur Spitze der Pyramide steht: 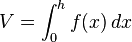
Da die Schnittfläche 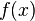 an der Stelle x durch eine zentrische Streckung der Grundfläche A mit dem Faktor
an der Stelle x durch eine zentrische Streckung der Grundfläche A mit dem Faktor 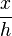 entsteht, ist also
entsteht, ist also 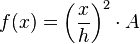 und damit:
und damit: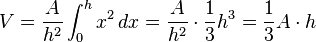 . (Keine Angst, dies ist kein Bestandteil der Veranstaltung sondern einfach nur eine gute Übung mit dem Formeleditor--Schnirch 12:13, 10. Okt. 2011 (CEST))
. (Keine Angst, dies ist kein Bestandteil der Veranstaltung sondern einfach nur eine gute Übung mit dem Formeleditor--Schnirch 12:13, 10. Okt. 2011 (CEST))
Beispiel für das Einbinden einer GeoGebra-Applikation
- Die Quelldatei gibt es hier: http://www.ph-heidelberg.de/wp/schnirch/GeoGebra/Spiegel.ggb
- Hilfe für das Einbinden einer GeoGebra-Applikation
Falls nichts angezeigt wird, können Sie mit folgendem Link den Servercache leeren.

