Winkel und Winkelmessung: Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (Die Seite wurde neu angelegt: = Winkel und Winkelmessung = == Begriff des Winkels == === Identifizieren von Winkeln === ==== Repräsentanten und Gegenrepräsentanten ==== In welchen Fällen sind die...) |
*m.g.* (Diskussion | Beiträge) (→Beweis von satz V.1) |
||
| (47 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 28: | Zeile 28: | ||
Aufgabe: Ergänzen Sie Tabelle 1 durch weitere Repräsentanten bzw. Gegenrepräsentanten zur Erarbeitung des Winkelbegriffs. | Aufgabe: Ergänzen Sie Tabelle 1 durch weitere Repräsentanten bzw. Gegenrepräsentanten zur Erarbeitung des Winkelbegriffs. | ||
| + | |||
| + | [http://www.ph-heidelberg.de/wp/gieding/Lehre/didaktik_5_8/flash/Trapez_Erarbeitung_drag.html Zum besseren Verständnis: Analoge Erarbeitung des Begriffs Trapez:] | ||
=== Realisieren von Winkeln === | === Realisieren von Winkeln === | ||
| Zeile 74: | Zeile 76: | ||
|} | |} | ||
| + | ==== Die Idee des gerichteten Winkels ==== | ||
| + | Gerichtete Winkel werden in der Einführung in die Geometrie keine Rolle spielen. Trotzdem dürfen Sie hier ergänzen, was denn ein gerichtetet Winkel wäre. | ||
| + | |||
=== Das Innere eines Winkels === | === Das Innere eines Winkels === | ||
| + | ==== So ist es zu verstehen ==== | ||
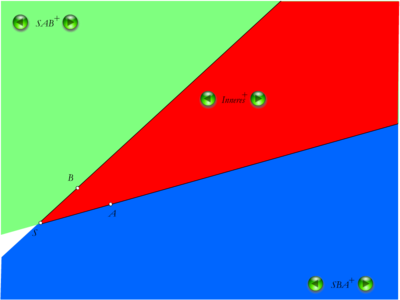
| + | [[Bild:Inneres_winkel.png | 400 px]] | ||
| + | |||
| + | [http://www.ph-heidelberg.de/wp/gieding/lehre/Geometrieeinfuehrung/Wiki/Flash/Inneres_eines_Winkels.htm Flashapplikation] | ||
| + | ==== Definition des Inneren eines Winkels ==== | ||
| + | ===== Definition V.2: (Inneres eines Winkels) ===== | ||
| + | ::Das Innere eines Winkels <math>\angle ASB</math> ist der Schnitt ...der beiden Halbebenen <math>\ SA,B^+</math> und <math>\ SB,A^+</math> | ||
| + | --[[Benutzer:Principella|Principella]] 10:47, 12. Jun. 2010 (UTC) | ||
| + | Passt nicht ganz: <math>\ SB,A^-</math> ist das so gewollt oder ein Tippfehler? --[[Benutzer:*m.g.*|*m.g.*]] 14:03, 13. Jun. 2010 (UTC) | ||
| + | |||
| + | ===== Satz V.1 ===== | ||
| + | :: Das Innere eines Winkels ist konvex. | ||
| + | ===== Beweis von Satz V.1 ===== | ||
| + | ::trivial entsprechend Satz IV., Satz IV.3 und der Definition V.2 | ||
| + | |||
| + | ==== Überstumpfe Winkel? ==== | ||
| + | Bemerkung: Entsprechend Definition V.2 beinhaltet unsere Geometrie keine überstumpfen Winkel. | ||
| + | == Scheitelwinkel und Nebenwinkel == | ||
| + | === Scheitelwinkel === | ||
| + | ==== Beispiele und Gegenbeispiele ==== | ||
| + | ==== Definition ==== | ||
| + | ===== Definition V.3: (Scheitelwinkel) ===== | ||
| + | ::Die Winkel <math>\angle SA^+,SB^+</math> und <math>\angle SA^-,SB^-</math> sind Scheitelwinkel. | ||
| + | |||
| + | === Nebenwinkel === | ||
| + | ==== Beispiele und Gegenbeispiele ==== | ||
| + | ==== Definition ==== | ||
| + | ===== Definition V.4: (Nebenwinkel) ===== | ||
| + | ::Die Winkel <math>\angle SA^+,SB^+</math> und <math>\angle SA^-,SB^+</math> sind Nebenwinkel. | ||
| + | |||
| + | == Winkelmessung == | ||
| + | === Das Winkelmaß === | ||
| + | ==== Was bedeutet es, die Größe eines Winkels zu messen? ==== | ||
| + | |||
| + | {| class="wikitable center" | ||
| + | |- | ||
| + | | Länge einer Strecke || Größe eines Winkels | ||
| + | |- | ||
| + | | nichtnegative reelle Zahl || reelle Zahl zwischen 0 und 180 | ||
| + | |} | ||
| + | |||
| + | ==== Das Winkelmaßaxiom ==== | ||
| + | ===== Axiom IV.1 (Winkelmaßaxiom) ===== | ||
| + | ::Zu jedem Winkel <math>\ \alpha</math> gibt es genau eine reelle Zahl <math>\ \omega</math> zwischen 0 und 180. | ||
| + | |||
| + | =====Definition V.4: (Größe eines Winkels) ===== | ||
| + | :: Die Zahl <math>\ \omega</math>, die entsprechend des Winkelmaßaxioms einem jeden Winkel <math>\ \alpha</math> eindeutig zugeordnet werden kann, wird die Größe oder das Maß von <math>\ \alpha</math> genannt.<br />In Zeichen: <math>\omega = \left| \alpha \right|</math>. | ||
| + | |||
| + | === Winkelkonstruktion === | ||
| + | ==== Existenz und Eindeutigkeit des Winkelantragens ==== | ||
| + | ===== Axiom IV.2: (Winkelkonstruktionsaxiom) ===== | ||
| + | :: Es sei <math>\ g \equiv SA</math> eine Gerade in der Ebene <math>\ \Epsilon</math>. Zu jedem Winkel <math>\ \alpha</math> gibt es in jeder der beiden durch <math>\ g</math> bestimmten Halbebenen der Ebene <math>\ \Epsilon</math> genau einen Strahl <math>\ SB^+</math> mit <math>\ \left| \alpha \right| = \left| \angle ASB \right|</math> | ||
| + | === Winkeladdition === | ||
| + | ===== Axiom IV.3: (Winkeladditionsaxiom)===== | ||
| + | ::Wenn der Punkt <math>\ P</math> zum Inneren des Winkels <math>\ \angle ASB</math> gehört, dann gilt <math>\ \left| \angle ASP \right| + \left| \angle PSB \right| = \left| \angle ASB \right|</math>. | ||
| + | ===== Satz V.2 ===== | ||
| + | ::Wenn der Punkt <math>\ P</math> im Inneren des Winkels <math>\ \angle ASB</math> liegt, dann ist die Größe der beiden Teilwinkel <math>\ \angle ASP</math> und <math>\ \angle PSB</math> jeweils kleiner als die Größe des Winkels <math>\ \angle ASB</math>. | ||
| + | ===== Beweis von Satz V.2 ===== | ||
| + | |||
| + | === Rechte Winkel === | ||
| + | ===== Definition V.5 : (Rechter Winkel) ===== | ||
| + | ::Wenn ein Winkel die selbe Größe wie einer seiner Nebenwinkel hat, so ist er ein rechter Winkel. | ||
| + | |||
| + | ===== Definition V.6 : (Supplementärwinkel) ===== | ||
| + | :: Zwei Winkel, deren Größen zusammen 180 ergeben, sind supplementär. | ||
| + | |||
| + | ===== Axiom IV.4: (Supplementaxiom) ===== | ||
| + | ::Nebenwinkel sind supplementär. | ||
| + | ===== Satz V. : (Existenz von rechten Winkeln) ===== | ||
| + | ::Es gibt rechte Winkel. | ||
Aktuelle Version vom 14. Juni 2010, 03:56 Uhr
Inhaltsverzeichnis
|
Winkel und Winkelmessung
Begriff des Winkels
Identifizieren von Winkeln
Repräsentanten und Gegenrepräsentanten
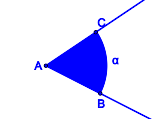
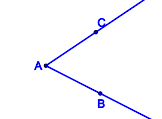
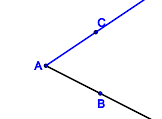
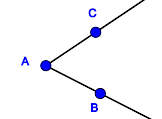
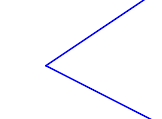
In welchen Fällen sind die jeweils blau gefärbten Punktmengen Modelle für Winkel?
 |
 |
 |
|
| Punktmenge 1 | Punktmenge 2 | Punktmenge 3 | Punktmenge 4 |
 |
 |
 |
|
| Punktmenge 5 | Punktmenge 6 | Punktmenge 7 | Punktmenge 8 |
Tabelle 1
| Winkelmodell | kein Winkelmodell |
|---|---|
| Tragen Sie die Nummern der entsprechenden obigen Punktmengen ein. Begründen Sie für jede Nummer Ihre Wahl. |
Tragen Sie die Nummern der entsprechenden obigen Punktmengen ein. Begründen Sie für jede Nummer Ihre Wahl. |
Prozeß der Begriffserarbeitung als Generierung einer Klasseneinteilung
In der Didaktik bezeichnen wir die Art und Weise der Erarbeitung eines neuen Begriffs entsprechend obiger Tabelle als induktive Begriffserarbeitung: Eine gewisse Menge an Repräsentanten und Gegenrepräsentanten bezüglich des zu erarbeitenden Begriffs wird vorgegeben. Dann teilt man diese Menge in genau zwei Klassen ein. Die eine Klasse bilden alle Begriffsrepräsentanten, die ander Menge der Rest.
Aufgabe: Ergänzen Sie Tabelle 1 durch weitere Repräsentanten bzw. Gegenrepräsentanten zur Erarbeitung des Winkelbegriffs.
Zum besseren Verständnis: Analoge Erarbeitung des Begriffs Trapez:
Realisieren von Winkeln
Die Idee des konstruktiven Begriffserwerbs
Während beim induktiven Begriffserwerb das Ausgangsmaterial für den Schüler bereits vorgefertigt wurde, generiert er es sich beim konstruktiven Begriffserwerb selbst. Der gute Lehrer läßt in der Regel beide Varianten zur Anwendung kommen.
Konstruktion eines Winkels
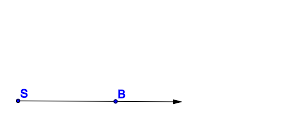
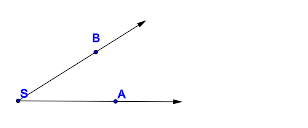
Aufgabe: Zeichne einen Winkel
Lösung:
| Konstruktionsschritt | Beschreibung |
|---|---|
|
Zeichne einen ... |
|
Zeichne einen zweiten ..., der |
Definition des Winkelbegriffs
Definition V.1: (Winkel)
- Ein Winkel ist ein Paar .... .
- ... heißt der Scheitelpunkt von ...
- ... sind die Schenkel von ...
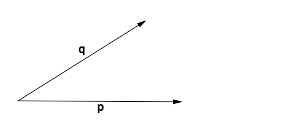
Arten, Winkel zu beschreiben
| Beispiel | Beschreibung | in Zeichen | Quelltext in Tex |
|---|---|---|---|
|
Winkel, der aus den beiden Strahlen  und und 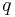 besteht. besteht.
|
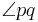
|
\angle pq |
|
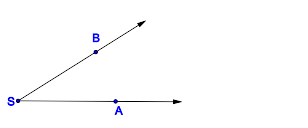
Winkel, der aus den beiden Strahlen 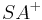 und und 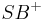 besteht. besteht.
|

|
\angle ASB |
Die Idee des gerichteten Winkels
Gerichtete Winkel werden in der Einführung in die Geometrie keine Rolle spielen. Trotzdem dürfen Sie hier ergänzen, was denn ein gerichtetet Winkel wäre.
Das Innere eines Winkels
So ist es zu verstehen
Definition des Inneren eines Winkels
Definition V.2: (Inneres eines Winkels)
- Das Innere eines Winkels
 ist der Schnitt ...der beiden Halbebenen
ist der Schnitt ...der beiden Halbebenen 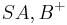 und
und 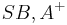
- Das Innere eines Winkels
--Principella 10:47, 12. Jun. 2010 (UTC)
Passt nicht ganz: 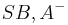 ist das so gewollt oder ein Tippfehler? --*m.g.* 14:03, 13. Jun. 2010 (UTC)
ist das so gewollt oder ein Tippfehler? --*m.g.* 14:03, 13. Jun. 2010 (UTC)
Satz V.1
- Das Innere eines Winkels ist konvex.
Beweis von Satz V.1
- trivial entsprechend Satz IV., Satz IV.3 und der Definition V.2
Überstumpfe Winkel?
Bemerkung: Entsprechend Definition V.2 beinhaltet unsere Geometrie keine überstumpfen Winkel.
Scheitelwinkel und Nebenwinkel
Scheitelwinkel
Beispiele und Gegenbeispiele
Definition
Definition V.3: (Scheitelwinkel)
- Die Winkel
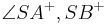 und
und 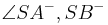 sind Scheitelwinkel.
sind Scheitelwinkel.
- Die Winkel
Nebenwinkel
Beispiele und Gegenbeispiele
Definition
Definition V.4: (Nebenwinkel)
- Die Winkel
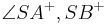 und
und 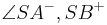 sind Nebenwinkel.
sind Nebenwinkel.
- Die Winkel
Winkelmessung
Das Winkelmaß
Was bedeutet es, die Größe eines Winkels zu messen?
| Länge einer Strecke | Größe eines Winkels |
| nichtnegative reelle Zahl | reelle Zahl zwischen 0 und 180 |
Das Winkelmaßaxiom
Axiom IV.1 (Winkelmaßaxiom)
- Zu jedem Winkel
 gibt es genau eine reelle Zahl
gibt es genau eine reelle Zahl 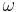 zwischen 0 und 180.
zwischen 0 und 180.
- Zu jedem Winkel
Definition V.4: (Größe eines Winkels)
- Die Zahl
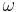 , die entsprechend des Winkelmaßaxioms einem jeden Winkel
, die entsprechend des Winkelmaßaxioms einem jeden Winkel  eindeutig zugeordnet werden kann, wird die Größe oder das Maß von
eindeutig zugeordnet werden kann, wird die Größe oder das Maß von  genannt.
genannt.
In Zeichen: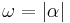 .
.
- Die Zahl
Winkelkonstruktion
Existenz und Eindeutigkeit des Winkelantragens
Axiom IV.2: (Winkelkonstruktionsaxiom)
- Es sei
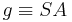 eine Gerade in der Ebene
eine Gerade in der Ebene  . Zu jedem Winkel
. Zu jedem Winkel  gibt es in jeder der beiden durch
gibt es in jeder der beiden durch  bestimmten Halbebenen der Ebene
bestimmten Halbebenen der Ebene  genau einen Strahl
genau einen Strahl 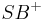 mit
mit 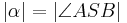
- Es sei
Winkeladdition
Axiom IV.3: (Winkeladditionsaxiom)
- Wenn der Punkt
 zum Inneren des Winkels
zum Inneren des Winkels  gehört, dann gilt
gehört, dann gilt 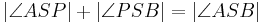 .
.
- Wenn der Punkt
Satz V.2
- Wenn der Punkt
 im Inneren des Winkels
im Inneren des Winkels  liegt, dann ist die Größe der beiden Teilwinkel
liegt, dann ist die Größe der beiden Teilwinkel 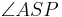 und
und 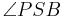 jeweils kleiner als die Größe des Winkels
jeweils kleiner als die Größe des Winkels  .
.
- Wenn der Punkt
Beweis von Satz V.2
Rechte Winkel
Definition V.5 : (Rechter Winkel)
- Wenn ein Winkel die selbe Größe wie einer seiner Nebenwinkel hat, so ist er ein rechter Winkel.
Definition V.6 : (Supplementärwinkel)
- Zwei Winkel, deren Größen zusammen 180 ergeben, sind supplementär.
Axiom IV.4: (Supplementaxiom)
- Nebenwinkel sind supplementär.
Satz V. : (Existenz von rechten Winkeln)
- Es gibt rechte Winkel.