Lösung von Aufgabe 6.4: Unterschied zwischen den Versionen
(→Vier) |
Hasekm (Diskussion | Beiträge) |
||
| (9 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 125: | Zeile 125: | ||
Ich würde sagen es gibt 4 Fälle zu unterscheiden, denn A,B und C könnten auch auf der Ebene E1 liegen.. | Ich würde sagen es gibt 4 Fälle zu unterscheiden, denn A,B und C könnten auch auf der Ebene E1 liegen.. | ||
| − | --[[Benutzer:Principella|Principella]] 19:24, 10. Jun. 2010 | + | --[[Benutzer:Principella|Principella]] 19:24, 10. Jun. 2010 |
== '''Fünf''' == | == '''Fünf''' == | ||
| Zeile 163: | Zeile 163: | ||
:Das was danach kommt, find ich auch logisch. Nur hab ich gedacht: Ein bisschen abgewandelt wäre das vielleicht schon der Beweis, dass eine Ebene unendlich viele (oder überabzählbar viele? Ich hab keine Ahnung.) Punkte enthält. Du hast es ja mit Axiom III/1 begründet und der Satz heißt Satz I/7. Das legt die Vermutung nahe, dass man es mit den Axiomen I/0 bis I/7 beweisen kann. Ob das so ist - keine Ahnung. Aber ich finde deine Argumentation einwandfrei. | :Das was danach kommt, find ich auch logisch. Nur hab ich gedacht: Ein bisschen abgewandelt wäre das vielleicht schon der Beweis, dass eine Ebene unendlich viele (oder überabzählbar viele? Ich hab keine Ahnung.) Punkte enthält. Du hast es ja mit Axiom III/1 begründet und der Satz heißt Satz I/7. Das legt die Vermutung nahe, dass man es mit den Axiomen I/0 bis I/7 beweisen kann. Ob das so ist - keine Ahnung. Aber ich finde deine Argumentation einwandfrei. | ||
:--[[Benutzer:Sternchen|Sternchen]] 16:03, 10. Jun. 2010 (UTC) | :--[[Benutzer:Sternchen|Sternchen]] 16:03, 10. Jun. 2010 (UTC) | ||
| + | |||
| + | Ich würde auch gerne wissen ob der Beweis von TheGeosi korrekt ist und wenn nicht warum?????????? | ||
| + | --[[Benutzer:Principella|Principella]] 15:15, 21. Jun. 2010 (UTC) | ||
| + | |||
| + | |||
| + | |||
| + | == Neuer Versuch == | ||
| + | |||
| + | |||
| + | Voraussetzung: Gegeben sein eine Ebene E<br /> | ||
| + | |||
| + | Behauptung: Es existieren wenigstens 3 verschiedene Punkte, die zu E gehören. | ||
| + | |||
| + | |||
| + | Beweis: | ||
| + | |||
| + | Fälle: | ||
| + | |||
| + | |||
| + | 1. A,B,C liegen in der Ebene E<br /> | ||
| + | 2. Genau zwei der drei Punkte liegen in der Ebene E (o.B.d.A. seien das Punkt A und Punkt B)<br /> | ||
| + | 3. Genau einer der drei liegen in Ebene E (o.B.d.A. sei das der Punkt A)<br /> | ||
| + | 4. Keiner der drei Punkte liegt in der Ebene E.<br /> | ||
| + | <br /> | ||
| + | Der Fall, dass alle vier Punkte in der Ebene liegen ist nicht möglich, da sie sonst alle komplanar wären, dies wir aber bereits in der vorangegangenen Sätzen der Übung ausgeschlossen. | ||
| + | <br /> | ||
| + | <br /> | ||
| + | Untersuchung von Fall 1:<br /> | ||
| + | <br /> | ||
| + | Nach dem Satz " Vier nicht komplanare Punkte gibt es keine 3 kollinearen Punkte, smit greift Axiom I/4<br /> | ||
| + | <br /> | ||
| + | Untersuchung von Fall 2:<br /> | ||
| + | <br /> | ||
| + | Mit den Punkten A und B enthält die Ebene E ja bereits zwei verschiedene Punkte. Es bleibt noch nachzuweisen, dass sie Ebene E einen weiteren Punkt enthält. Hierzu nehmen wir an die Punkte B,C,D bestimmen zusammen eine eindeutige Ebene Z. Diese Ebene Z hat mit der Ebene E einen Punkt gemeinsam und zwar Punkt B. Nach dem Axiom I/6 müssen diese Ebenen einen weiteren gemeinsamen Punkt haben, dass sei der Punkt E. Es darf nicht der Punkt A sein, da sonst neben den Punkten B,C,D ja auch Punkt A in der Ebene Z enthalten wäre. Das wollen wir nicht, sonst wären ja alle vier komplanar. <br /> | ||
| + | <br /> | ||
| + | Untersuchung von Fall 3: <br /> | ||
| + | <br /> | ||
| + | Die drei Punkte B,C,D liegen außerhalb der Ebene E und bestimmen zusammen mit Punkt A eine eindeutig die folgenden Ebenen: | ||
| + | Ebene Z, die durch die Punkte A,B,D bestimmt ist und Ebene Y, die durch Punkt A,C,D bestimmt ist. Diese beiden Ebenen Z und Y sind nicht identisch. Sonst hätten wir ja schon wieder vier komplanare Punkt, wollen wir ja nicht. Damit haben sie nach dem Axoim I/6 noch einen weiteren Punkt gemeinsam, nämlich Punkt E. Somit haben sie zwei Punkt gemeinsam, A,D und E. Da es ja im Axiom I/6 heißt mindesten einen weitern Punkt, kann ich ja noch von einem weiteren gemeinsamen Punkt F ausgehen. So muss ich zeigen, dass die Punkte E und F nicht idetisch sind. | ||
| + | Dies mache ich indirekt, indem ich ganz einfach annehme sie seien idetisch =). Somit haben die Ebenen Z und Y die folgenden Punkte gemeinsam: A,D und E=F. Demnach sind die beiden Ebenen nach Axiom I/4 identisch, da es heißt 3 nkoll => genau eine Ebene. Widerspruch zum Axiom I/7. Somit eine Ebene mit drei Punkten, sogar zwei.<br /> | ||
| + | <br /> | ||
| + | Untersuchung von Fall 4:<br /> | ||
| + | <br /> | ||
| + | Wenn keiner der vier Punkte A,B,C,D in Ebene E ist. Gibt es nach Axiom I/4 wenigstens einen Punkt E der in der Ebene E enthalten ist. Dieser fall kann, dann analog wie bei Fall 3 weiter gehen, doch mit den Punkten E,B,C,D statt den Punkten A,B,C,D.<br /> | ||
| + | <br /> | ||
| + | Frage stimmt das oder hab ich mich verrannt und den Satz missverstanden?????? | ||
Aktuelle Version vom 14. Juli 2010, 09:55 Uhr
Beweisen Sie: Jede Ebene enthält wenigstens drei paarweise verschiedene Punkte.
Inhaltsverzeichnis |
Eins
Behauptung: Wenn eine Ebene E existiert, dann enthält sie wenigstens drei paarweise verschiedene Punkte A, B, C.
Vorraussetzung: Es existiert eine Ebene E mit A, B, C Element E
Annahme: A, B, C sind paarweise verschieden.
| Beweisschritt | Begründung |
| (1) komp (A,B,C) (2) A nicht identisch B B nicht identisch C |
1)nach Definition I/6 2)nach Satz I/7 |
=> A, B, C sind paarweise verschieden
Kommt uns ein wenig zu kurz vor. von Maude001 und Nicola
- Diskussion:Lösung_von_Aufgabe_6.4 wollte den Diskussionsfluss nicht unterbrechen und hab meine Bemerkungen in die Diskussion geschoben --*m.g.* 14:07, 9. Jun. 2010 (UTC)
Zwo
Behauptung:
Wenn eine Ebene  existiert, dann enthält sie wenigstens drei paarweise verschiedene Punkte A, B, C.
existiert, dann enthält sie wenigstens drei paarweise verschiedene Punkte A, B, C.
Vorraussetzung:
Es existiert eine Ebene  mit A, B, C
mit A, B, C 

Annahme:
A, B, C sind paarweise verschieden.
Diesen Satz I.7 ("Jede Ebene enthält (wenigstens) drei Punkte.") muss man bestimmt mit einer Fallunterscheidung beginnen.
Fall 1:
koll(A, B, C) <-> A, B, C  Gerade g
Dadurch ergibt sich ja (nach Vorraussetzung), dass A, B, C
Gerade g
Dadurch ergibt sich ja (nach Vorraussetzung), dass A, B, C 
 und (nach Fallunterscheidung) A, B, C
und (nach Fallunterscheidung) A, B, C  g. Dann greift Axiom I/5
g. Dann greift Axiom I/5
Wenn zwei Punkte einer Geraden g in einer Ebene E liegen, so gehört g zu E.
...hier sind es sogar alle drei Punkte.
Fall 2:
Je zwei Punkte sind kollinear.
o.B.d.A koll(A, B) -> A, B  Gerade g
Gerade g 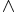 C
C 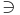 Gerade g
Gerade g
nkoll(A, B, C)
Nun besagt Axiom I/4
Zu je drei nichtkollinearen Punkten gibt es genau eine Ebene, die diese drei Punkte enthält.
Reicht das als Begründung für Satz I.7 ?
Zusatz:
Deswegen brauchen wir den Fall 3 nicht, wonach alle drei Punkte nichtkollinear sind. Geht nicht!
AXIOM I/1(Axiom von der Geraden)
Zu zwei beliebigen verschiedenen Punkten gibt es genau eine Gerade, die die beiden Punkte enthält.
Drei
Ich habe ein Problem mit eurer Voraussetzung. Dass die Ebene drei Punkte enthält, soll man ja beweisen. Ich würde es eher so formulieren:
- Voraussetzung:
 ist eine Ebene.
ist eine Ebene.
- Behauptung:
 enthält wenigstens drei verschiedene Punkte.
enthält wenigstens drei verschiedene Punkte.
- Das könnte man natürlich aufgliedern in:
 enthält wenigstens drei Punkte. Und in: Diese drei Punkte sind paarweise verschieden. Damit habt ihr schon recht. Aber in eurer Argumentation kommt nicht vor, dass es ja auch Ebenen geben könnte, die nur einen oder zwei Punkte enthalten. Und genau das soll man ja widerlegen.
enthält wenigstens drei Punkte. Und in: Diese drei Punkte sind paarweise verschieden. Damit habt ihr schon recht. Aber in eurer Argumentation kommt nicht vor, dass es ja auch Ebenen geben könnte, die nur einen oder zwei Punkte enthalten. Und genau das soll man ja widerlegen.
- Das könnte man natürlich aufgliedern in:
Übrigens ergibt sich direkt aus Axiom I/4, dass es keine Ebene gibt, die keinen Punkt enthält. Da heißt es ja: "Jede Ebene enthält (wenigstens) einen Punkt." Aber wo kommen die anderen Punkte her? In Axiom I/4 heißt es ja, dass es zu drei nichtkollinearen Punkten genau eine Ebene gibt, die diese enthält, aber da steht nicht, dass es auch umgekehrt zu jeder Ebene drei Punkte gibt, die darin enthalten sind.
Ich stelle mir also eine Ebene 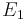 vor, die den Punkt
vor, die den Punkt  enthält. Einen Punkt muss sie ja schließlich nach Axiom I/4 enthalten. Dann weiß ich nach Axiom I/3, dass es wenigstens drei nichtkollineare Punkte gibt. Gehen wir davon aus,
enthält. Einen Punkt muss sie ja schließlich nach Axiom I/4 enthalten. Dann weiß ich nach Axiom I/3, dass es wenigstens drei nichtkollineare Punkte gibt. Gehen wir davon aus,  wäre einer davon und die anderen beiden hießen
wäre einer davon und die anderen beiden hießen  und
und  . Jetzt gibt es aber meines Erachtens zwei Möglichkeiten, wie Axiom I/4 erfüllt werden kann.
. Jetzt gibt es aber meines Erachtens zwei Möglichkeiten, wie Axiom I/4 erfüllt werden kann.
- 1.Fall: Die gesuchte Ebene, die zu diesen drei Punkten gehört ist
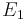 . Problem geklärt,
. Problem geklärt, 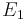 enthält drei Punkte. Prima.
enthält drei Punkte. Prima.
- 2.Fall: Die gesuchte Ebene ist
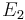 , wobei gilt
, wobei gilt 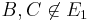 , also
, also 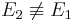 . Womit immer noch das Problem besteht, wo die anderen Punkte für
. Womit immer noch das Problem besteht, wo die anderen Punkte für 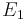 herkommen.
herkommen.
Es geht bestimmt irgendwie, aber ich bin noch nicht draufgekommen.
--Sternchen 12:32, 5. Jun. 2010 (UTC)
Vier
zz: Jede Ebene enthält wenigstens 3 paarweise verschiedene Punkte.
Beweisidee:
Ausgangspunkt ist Axiom I/7 : Es gibt 4 Punkte, die nicht in ein und derselben Ebene liegen. Seien dies die Punkte A,B,C und D. Ferner sei E1 eine Ebene.
Es gilt 3 Fälle zu unterscheiden:
Fall 1: A,B gehört zu E1 und C,D gehört nicht zu E1
Fall 2: A gehört zu E1 und B,C,D gehören nicht zu E1
Fall 3: keine der 4 Punkte A,B,C,D gehören zu E1
BEWEIS:
Fall 1:
1) nkomp(A,B,C,D) -> nkoll(A,B,C) (Satz und Axiom I/7)
2) Es existiert zu A,B,C eine Ebene F, sodass A,B und C in F liegen (Axiom I/4)
3) Nun gilt, dass A sowohl in E1 als auch in F enthalten ist (Voraussetzung und 2))
4) Es existiert ein Punkt S mit: S ist sowohl in E1 als auch in F enhalten (Axiom I/6 und 3))
5) A, B und S sind in E1 enthalten ( 4)und Voraussetzung, dass A und B in E1 liegt)
Fall 2 funktioniert analog:
Es existieren zu den Punktemengen {A,B,C}, {A,B,D} jeweils eine Ebene. Seien diese E2 und E3. Jede dieser Ebenen
haben den Punkt A mit E1 gemeinsam. Laut Axiom I/6 gibt es dann zwei weitere Punkte P1 und P2, die sowohl in diesen Ebenen als auch in E1 enthalten sind. Folglich enthält E1 die Punkte A, P1 und P2.
In den beiden bisherigen Fällen hat E1 also mindestens 3 Punkte.
Fall 3 konnte ich leider nicht lösen.
Ich würde sagen es gibt 4 Fälle zu unterscheiden, denn A,B und C könnten auch auf der Ebene E1 liegen..
--Principella 19:24, 10. Jun. 2010
Fünf
Vor: Ebene E
Beh: Ebene enthält drei Punkte A,B und C, die paarweise verschieden sind
(1) Es gibt einen Punkt A auf der Ebene E (Axiom I/4)
(2) Die Ebenen E und E haben den Punkt A gemeinsam (Trivial)
(3) E und E haben einen weiteren Punkt B gemeinsam (Axiom I/6)
(4) => A und B gehören zu E
(5) Es gibt eine Gerade g, die durch die Punkte A und B geht (Aciom I/1)
(6) Es gibt einen Punkt C, der auf dem Strahl AB+ liegt und für den gilt: |AC| = d und P ungelich A,B(Axiom III/1)
(7) C ist Element von E (Axiom I/5)
(8) => A, B und C sind Element von E und paarweise verschieden ((8))
q.e.d.
was haltet ihr davon?
--TheGeosi 14:32, 10. Jun. 2010 (UTC)
- Ich find's klasse. Vor allem, wie du auf den Punkt B gekommen bist. Das ist bestechend einfach.
- Das was danach kommt, find ich auch logisch. Nur hab ich gedacht: Ein bisschen abgewandelt wäre das vielleicht schon der Beweis, dass eine Ebene unendlich viele (oder überabzählbar viele? Ich hab keine Ahnung.) Punkte enthält. Du hast es ja mit Axiom III/1 begründet und der Satz heißt Satz I/7. Das legt die Vermutung nahe, dass man es mit den Axiomen I/0 bis I/7 beweisen kann. Ob das so ist - keine Ahnung. Aber ich finde deine Argumentation einwandfrei.
- --Sternchen 16:03, 10. Jun. 2010 (UTC)
Ich würde auch gerne wissen ob der Beweis von TheGeosi korrekt ist und wenn nicht warum?????????? --Principella 15:15, 21. Jun. 2010 (UTC)
Neuer Versuch
Voraussetzung: Gegeben sein eine Ebene E
Behauptung: Es existieren wenigstens 3 verschiedene Punkte, die zu E gehören.
Beweis:
Fälle:
1. A,B,C liegen in der Ebene E
2. Genau zwei der drei Punkte liegen in der Ebene E (o.B.d.A. seien das Punkt A und Punkt B)
3. Genau einer der drei liegen in Ebene E (o.B.d.A. sei das der Punkt A)
4. Keiner der drei Punkte liegt in der Ebene E.
Der Fall, dass alle vier Punkte in der Ebene liegen ist nicht möglich, da sie sonst alle komplanar wären, dies wir aber bereits in der vorangegangenen Sätzen der Übung ausgeschlossen.
Untersuchung von Fall 1:
Nach dem Satz " Vier nicht komplanare Punkte gibt es keine 3 kollinearen Punkte, smit greift Axiom I/4
Untersuchung von Fall 2:
Mit den Punkten A und B enthält die Ebene E ja bereits zwei verschiedene Punkte. Es bleibt noch nachzuweisen, dass sie Ebene E einen weiteren Punkt enthält. Hierzu nehmen wir an die Punkte B,C,D bestimmen zusammen eine eindeutige Ebene Z. Diese Ebene Z hat mit der Ebene E einen Punkt gemeinsam und zwar Punkt B. Nach dem Axiom I/6 müssen diese Ebenen einen weiteren gemeinsamen Punkt haben, dass sei der Punkt E. Es darf nicht der Punkt A sein, da sonst neben den Punkten B,C,D ja auch Punkt A in der Ebene Z enthalten wäre. Das wollen wir nicht, sonst wären ja alle vier komplanar.
Untersuchung von Fall 3:
Die drei Punkte B,C,D liegen außerhalb der Ebene E und bestimmen zusammen mit Punkt A eine eindeutig die folgenden Ebenen:
Ebene Z, die durch die Punkte A,B,D bestimmt ist und Ebene Y, die durch Punkt A,C,D bestimmt ist. Diese beiden Ebenen Z und Y sind nicht identisch. Sonst hätten wir ja schon wieder vier komplanare Punkt, wollen wir ja nicht. Damit haben sie nach dem Axoim I/6 noch einen weiteren Punkt gemeinsam, nämlich Punkt E. Somit haben sie zwei Punkt gemeinsam, A,D und E. Da es ja im Axiom I/6 heißt mindesten einen weitern Punkt, kann ich ja noch von einem weiteren gemeinsamen Punkt F ausgehen. So muss ich zeigen, dass die Punkte E und F nicht idetisch sind.
Dies mache ich indirekt, indem ich ganz einfach annehme sie seien idetisch =). Somit haben die Ebenen Z und Y die folgenden Punkte gemeinsam: A,D und E=F. Demnach sind die beiden Ebenen nach Axiom I/4 identisch, da es heißt 3 nkoll => genau eine Ebene. Widerspruch zum Axiom I/7. Somit eine Ebene mit drei Punkten, sogar zwei.
Untersuchung von Fall 4:
Wenn keiner der vier Punkte A,B,C,D in Ebene E ist. Gibt es nach Axiom I/4 wenigstens einen Punkt E der in der Ebene E enthalten ist. Dieser fall kann, dann analog wie bei Fall 3 weiter gehen, doch mit den Punkten E,B,C,D statt den Punkten A,B,C,D.
Frage stimmt das oder hab ich mich verrannt und den Satz missverstanden??????

