Serie 02 12 13: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(→Lösung) |
|||
| (4 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 7: | Zeile 7: | ||
b) <math> y + \frac{1}{2}=\frac{1}{2}(x-2)</math> <br /> | b) <math> y + \frac{1}{2}=\frac{1}{2}(x-2)</math> <br /> | ||
c) <math>PQ</math> mit <math>P(3|1)</math> und <math>Q(-1|\frac{1}{2})</math> <br /> | c) <math>PQ</math> mit <math>P(3|1)</math> und <math>Q(-1|\frac{1}{2})</math> <br /> | ||
| + | |||
| + | |||
| + | =Aufgabe 3= | ||
| + | |||
| + | Es seien <math>P_1(x_1|y_1)</math> und <math>P_2(x_2|y_2)</math> zwei beliebige voneinander verschiedene Punkte einer Geraden mit der Gleichung | ||
| + | <math>ax+by=c</math> (a,b,c<math>\in \mathbb{R}</math>, <math>a\neq 0</math> oder <math>\neq 0 </math>). <br /> | ||
| + | Zeigen Sie, das gilt: | ||
| + | |||
| + | <math>\frac{y_2-y_1}{x_2-x_1}=-\frac{a}{b}=m</math> | ||
| + | |||
| + | =Aufgabe 4= | ||
| + | |||
| + | Bestimmen Sie ein lineares Gleichungssystem (bestehend aus zwei Gleichungen), das die Gerade durch die Punkte <math>P(0|5|-2)</math> und <math>Q(14|3|2)</math> beschreibt. | ||
| + | |||
| + | =Lösung= | ||
| + | [[Lösungen zu den Aufgaben 2]] | ||
Aktuelle Version vom 27. Dezember 2012, 11:09 Uhr
Inhaltsverzeichnis |
Aufgabe 1
Auf einem Pixelbilschirm soll ein "Kreis" mit dem Radius r=10 Pixel in Mittelpunktslage generiert werden. Zur Berechnung der Pixel des zweiten Oktanten wird der Algorithmus von Bresenham verwendet. Man bestimme die Koordinaten der Pixel, die der Algorithmus liefert.
Aufgabe 2
Berechnen Sie den Steigungswinkel folgender Geraden:
a)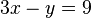 
b)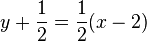 
c)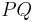 
mit 
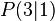und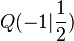 
Aufgabe 3
Es seien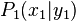 
und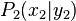 
zwei beliebige voneinander verschiedene Punkte einer Geraden mit der Gleichung
(a,b,c
, 
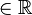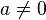oder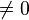 
).
Zeigen Sie, das gilt:
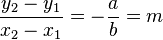
Aufgabe 4
Bestimmen Sie ein lineares Gleichungssystem (bestehend aus zwei Gleichungen), das die Gerade durch die Punkte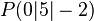 
und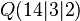 
beschreibt.
