Bewegungen (2012 13): Unterschied zwischen den Versionen
Jessy* (Diskussion | Beiträge) (→Beweis von Satz 1.5:) |
Gubbel (Diskussion | Beiträge) (→Injektivität) |
||
| (3 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 83: | Zeile 83: | ||
| (III) | | (III) | ||
| (I) und (II) widersprechen sich. | | (I) und (II) widersprechen sich. | ||
| − | | (I), (II)--[[Benutzer:Beveggie|Beveggie]] 16:17, 10. Nov. 2012 (CET) | + | | (I), (II), Definition Bewegung --[[Benutzer:Gubbel|Gubbel]] 19:02, 1. Mai 2013 (CEST) --[[Benutzer:Beveggie|Beveggie]] 16:17, 10. Nov. 2012 (CET) |
|} | |} | ||
| Zeile 134: | Zeile 134: | ||
|- | |- | ||
| (d) || Falls zwei Geraden, Strecken, Halbgeraden oder zwei verschiedene dieser Figuren einen Punkt <math>\ P</math> gemeinsam haben, so haben die Bildfiguren den Punkt <math>\ \beta(P)</math> gemeinsam. | | (d) || Falls zwei Geraden, Strecken, Halbgeraden oder zwei verschiedene dieser Figuren einen Punkt <math>\ P</math> gemeinsam haben, so haben die Bildfiguren den Punkt <math>\ \beta(P)</math> gemeinsam. | ||
| + | |- | ||
| + | | (e) || Jede Halbebene mit einer Randgeraden g auf eine Halbebene mit der Randgeraden β(g). | ||
| + | |- | ||
| + | | (f) || Das Innere eines beliebigen Winkels wird auf das Innere des zugehörigen Bildwinkels abgebildet. | ||
|} | |} | ||
| Zeile 172: | Zeile 176: | ||
[[Bild:Winkeltreue.JPG|600px]] | [[Bild:Winkeltreue.JPG|600px]] | ||
| + | --[[Benutzer:Jessy*|Jessy*]] 09:48, 16. Nov. 2012 (CET)<br /><br /> | ||
| + | =====Satz 1.6:===== | ||
| + | Jede Bewegung ist durch ein Dreieck <math>\bar{ABC}</math> und dessen Bild <math>\bar{A'B'C'}</math> eindeutig bestimmt.<br /><br /> | ||
| + | =====Beweis von Satz 1.6:===== | ||
| + | [[Bild:Satz_1.6.JPG|700px]]<br /><br /> | ||
| + | --[[Benutzer:Jessy*|Jessy*]] 09:22, 12. Dez. 2012 (CET)<br /><br /> | ||
<!--- Was hier drunter steht muss stehen bleiben ---> | <!--- Was hier drunter steht muss stehen bleiben ---> | ||
|} | |} | ||
Aktuelle Version vom 1. Mai 2013, 18:02 Uhr
Der Begriff der BewegungDie GrundideenStarrheit und Kopieren
Abstraktion von den physikalischen GegebenheitenDie Materie scheint schwer genug zu sein. Wir werden unsere Betrachtungen auf eine einzige Ebene ε einschränken. Die Lochschablone ist nichts anderes als das Modell unserer Ebene. Leider muss jedes physikalische Modell, mit dem der Schüler auch noch konkret handelnd tätig werden soll, flächenmäßig beschränkt sein.Für den mathematischen Bewegungsbegriff abstrahieren wir von dieser Beschränktheit. Das ist uns eigentlich schon länger klar, soll an dieser Stelle jedoch noch einmal besonders hervorgehoben und betont werden. Hinter der Idee des Kopierens steckt nichts anderes als der mathematische Abbildungsbegriff. Jedem Original wird ein Bild zugeordnet. Der Definitionsbereich für unsere Abbildungen ist die gesamte Ebene. Ihr Bild ist sie selbst. Jeder Punkt der Ebene ε wird auf genau einen Punkt der Ebene ε abgebildet. Aus mathematischer Sicht ist es egal, ob unser Ebenenmodell aus Plastik oder Glas ist. Aus Gummi dürfte es allerdings nicht sein, denn Gummimatten sind mit Sicherheit nicht starr. Die Starrheit bedeutet nichts weiter, als dass zwei Originalpunkte denselben Abstand haben wie ihre Bildpunkte. Der Begriff der BewegungDefinitionDefinition 1.1: Bewegung
Eigenschaften von BewegungenSatz 1.1: (Bijektivität von Bewegungen)
Beweis von Satz 1.1VorüberlegungenEs sei Wir haben zu zeigen, dass und ist. SurjektivitätDie Surjektivität ergibt sich entsprechend der Definition 1.1 (Abbildung auf) InjektivitätAlle unsere folgenden Bemerkungen beziehen sich auf ein und dieselbe Ebene zu zeigen:
Wir entscheiden uns dafür, 3. zu zeigen. Wir führen den Beweis indirekt. (Ergänzen Sie den Beweis!)
Satz 1.2: (Abgeschlossenheit der Nacheinanderausführung von Bewegungen)
Beweis von Satz 1.2Zunächst ist allgemein bekannt, dass die NAF zweier Abbildungen eine Abbildung ist (s. Algebra I). Es seien Bleibt zu zeigen, dass die NAF zweier Bewegungen auch abstandserhaltend ist. --Jessy* 09:21, 16. Nov. 2012 (CET) Satz 1.3: (Zwischenrelation als Invariante von Bewegungen)
Beweis von Satz 1.3Es seien (*) zu zeigen: (**) Wir übersetzen zunächst (*):
entsprechend (**) haben wir zu zeigen, dass Den Rest können Sie alleine ... . --Jessy* 09:46, 7. Nov. 2012 (CET) Satz 1.4: (Geradentreue, Halgeradentreue, Streckentreue, Schnittpunkttreue bei Bewegungen)
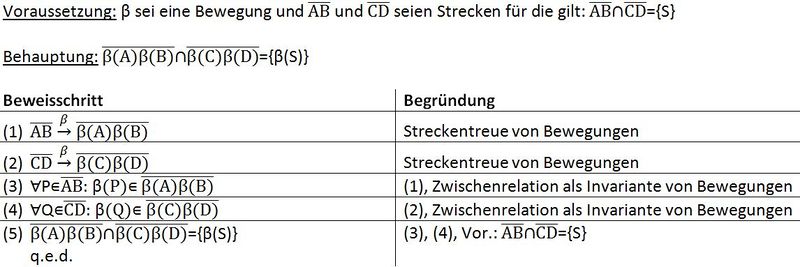
Beweis von Satz 1.4:
Beweis von (a) Beweis von (b) Beweis von (c) Beweis von (d) Die anderen Beweise zur Schnittpunkttreue müssten analog verlaufen... --Jessy* 09:36, 16. Nov. 2012 (CET) Satz 1.5: (Winkelgröße als Invariante bei Bewegungen)
Beweis von Satz 1.5:Abstandserhaltung von --Jessy* 09:48, 16. Nov. 2012 (CET) Satz 1.6:Jede Bewegung ist durch ein Dreieck Beweis von Satz 1.6:
|
 eine Bewegung, die die Ebene
eine Bewegung, die die Ebene  auf sich selbst abbildet.
auf sich selbst abbildet.
 . Wir verzichten deshalb darauf, die Zugehörigkeit der im folgenden verwendeten Punkte zu
. Wir verzichten deshalb darauf, die Zugehörigkeit der im folgenden verwendeten Punkte zu  kennzeichnen.
kennzeichnen.
 ist das Bild von maximal einem Punkt
ist das Bild von maximal einem Punkt  .
. haben nicht dasselbe Bild.
haben nicht dasselbe Bild.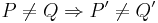
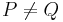
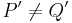

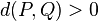
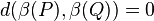
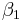 und
und 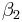 zwei Bewegungen.
zwei Bewegungen. 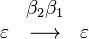 .
.

 drei paarweise verschiedene Punkte mit
drei paarweise verschiedene Punkte mit
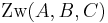 .
.
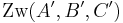
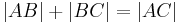
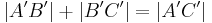 gilt.
gilt.

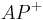 ist eine Halgerade mit dem Anfagspunkt
ist eine Halgerade mit dem Anfagspunkt 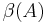 .
.
 ist die Strecke
ist die Strecke 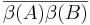
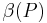 gemeinsam.
gemeinsam.



 gilt:
gilt:
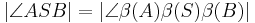
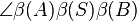

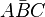 und dessen Bild
und dessen Bild 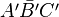 eindeutig bestimmt.
eindeutig bestimmt.

