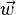Pfeilklassen 2012 13: Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (→Pfeilklassen) |
*m.g.* (Diskussion | Beiträge) (→Definition der Addition von Pfeilklassen) |
||
| (33 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 4: | Zeile 4: | ||
<!--- hier drüber nichts eintragen ---> | <!--- hier drüber nichts eintragen ---> | ||
=Pfeile= | =Pfeile= | ||
| − | Unter einem Pfeil versteht man eine gerichtete Strecke. Wir werden den | + | ==Probleme?== |
| + | (Unter einem Pfeil versteht man eine gerichtete Strecke. Wir werden den Begriff intuitiv gebrauchen.) | ||
| + | Offenbar ist es so, dass Ihnen die intuitive Verwendung des Begriffs ''Pfeil'' nicht ganz geheuer ist. Ich kann das verstehen. | ||
| + | Hier eine genauere Erläuterung:<br /> | ||
| + | ==Strecken== | ||
| + | Strecken kennen wir aus der Einführung in die Geometrie: | ||
| + | {{Definition|Strecke<br /> <math>A,B</math> seien zwei verschiedene Punkte. <math>\overline{AB}:=\left\{P|\operatorname{Zw}(A,P,B) \vee P=A \vee P=B \right\}</math>}} | ||
| + | |||
| + | Für Strecken gilt: <math>\overline{AB} \equiv \overline{BC}</math>. | ||
| + | |||
| + | Eine Strecke hat damit keinen Anfangspunkt. Keiner der beiden Punkte <math>A</math> und <math>B</math> ist dem anderen vorziehen. Beide heißen Endpunkte der Strecke <math>\overline{AB}</math>. | ||
| + | |||
| + | ==Pfeile== | ||
| + | Pfeile sind zunächst dasselbe wie Strecken: Eine Menge von Punkten, die zwischen zwei Punkten <math>A</math> und <math>B</math> liegen vereinigt mit der Menge die aus den beiden Endpunkten <math>A</math> und <math>B</math> besteht. Wir werden jetzt jedoch den erstgenannten Endpunkt vor dem zweitgenannten Endpunkt auszeichnen. Er wird Anfangspunkt genannt, der zweite Endpunkt heißt weiterhin Endpunkt. Anfangspunkt und Endpunkt einer solchen gerichteten Strecke bzw. eines solchen Pfeils bilden also ein geordnetes Paar. Die Reihenfolge ihrer Nennung ist damit nicht mehr beliebig. | ||
| + | |||
| + | {{Definition|Pfeil <math>\vec{AB}</math><br />Es seien <math>A</math> und <math>B</math> zwei (nicht notwendigerweise) verschiedene Punkte. Der Pfeil <math>\vec{AB}</math> ist das geordnete Paar <math>(A,B)</math>. <math>A</math> heißt Anfangspunkt des Pfeils <math>\vec{AB}</math>, <math>B</math> heißt Endpunkt des Pfeils <math>\vec{AB}</math>. Jedem Pfeil ist eine Punktmenge zugehörig, Es handelt sich dabei um die Menge der Punkte der Strecke <math>\overline{AB}</math>. Sollte der Anfangspunkt eines Pfeils mit dem Endpunkt dieses Pfeils zusammenfallen spricht man vom Nullpfeil <math>\vec{o}</math>. Zwei Pfeile <math>\vec{AB}</math> und <math>\vec{CD}</math> haben einen Punkt gemeinsam falls ihre Punktmengen einen Punkt gemeinsam haben.}} | ||
| + | |||
=Pfeilklassen= | =Pfeilklassen= | ||
| − | {{Definition|P. | + | ==Definition parallelgleich== |
| + | <ggb_applet width="510" height="463" version="4.2" ggbBase64="UEsDBBQACAgIAAp4jEEAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAgIAAp4jEEAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s7Vjfb9s2EH5u/4qDEOxliUzqp93ZLRIHxQqkXbFkRTHshZZom40saSJlO137v+9ISrZsNwvSpO3LkjgUyeMd77u7j5SHL9aLDJa8kqLIRw51iQM8T4pU5LORU6vpSd958fzpcMaLGZ9UDKZFtWBq5ASu52zXYc8N9FqRjpzphHMvIJOTOPXDkyBM+id9Fk9OOJkOSBIROohQEtZSPMuLN2zBZckSfpnM+YJdFAlTRuVcqfJZr7dardzWuFtUs95sNnHXMnUAN57LkdM8PEN1O4tWvhH3CKG9968vrPoTkUvF8oQ7oJ2qxfOnT4YrkafFClYiVfORE/qxA3MuZnP0MiK4054WKtHVkidKLLnEpZ2u8VktSseIsVzPP7FPkG3ccSAVS5HyauQQ14+9wB8EcT/sB7HvQFEJnqtGkjYWe62u4VLwlVWqn4y9gAxwm0shxSTjCDnLJPok8mmFeOJ2qhq7Ut1kfMKqtr/dDT3GXxQQH7nWhU5aEEaONyDHHo2PY0KOw7DxvmvYAVUUmdFKIBzAp0/gEY/AsW6obTxsoshOETtGfNt4tglsE1qZwC4PrGhgZQIrE/j/4WfT3zraDOx42vrpd/2k6J/+YISPA3LoZ7/jJ9VOfAKqd28aH/S+qdm/boKmG9lubBpKbEObyb7+Z/CKHuiR/1Ue0Y5Vmw+3Gz3Il9ZiSO9h0XuQnxsvvS956YW3ePlAcFujNOwYRVvmz3wOTPr38vNWaO9hMQoeUvtfYTAm38PgsNcy3bCpPZBzLdukq+ILqVnHHxjiAQohFmYUI0+EQAfYxLpAPaAhBCF2aR8i3cbg65oMwIc+aDnqg6GXsI//AlOvEYSoSw/GtnDBDyD0gRpSCgCpCAyxIcl5PkqEIYS4SFun2qwfQRBhx+9DgBvUlBZr2vBxHfbRuAc+BV+vpTF4EUQexJoWaaDZMurrvaNSDyICkV6KvIicaPkQV/TB195ghpeFFBtw5zwrN1ExOIq8rNUOdskibR9VsSedFsn12R7WnEnVPqMQHkbbA88eTjvn4ZNhxiY8w0vDpU4DgCXLdAUb/dMiV9CmgGfHZhUr5yKRl1wpXCXhA1uyC6b4+iVKy3aDxrQ5poe8TjKRCpa/wxzRKrRC2JzampfaUzvwQ2slKYoqvbyRmDiw/pNXBZIJDV3S/Rk4cGOn/P0pBFomTKd8SHZnsOJvbpmi1jRfblxja75xCGaVuSJtO6/kWZFth8pC5GrMSlVX5gqGLFhpr07zWcYNuIZX8TaTXE+K9aVF1be6rm5K7BG7g8lsXGRFBViRXhiiQNNObGtk9NY2UsTIECNB2jCJdDNPB56RMO3EtkYK42631rhKWzcpac0IaXgEldssa4lXZ42+HNW5UBdtR4nkunGV2gVv6sUEE67JyF2d9LF0Dnt7OTa85lXOM5tJOQazLmppU3uTnk+GteRvmZqf5unvfIY1+ZZpWlSo2oput5zyRCxwoR1vwGM6sH/gVu1oymcVb13MzLXXQmtmSTevD4aNqpdVsXiVL68wa/a2Ouy1/gxlUolSZydMkKev+Tb/UiEZsnzaXYfOS/Qi0YyDQCoNogOsVvOiMjdbrFtd2nDOP3INKnIlFrou2owv8GYLyiSmye1NgE7NhVlHAorJB6SSzclh57e44fQtSQosK+dMX6kbCDJ2g+a7oBhtv02nkitYj5wTT9cu7jboTL8uUr5DWSzHQBl3kTtKmzIl5zbbrDP4UKI1U6SdbDChkcYSdWNjirgxntcf7duVfZnQQOjS3TFqRw+DjWSgd2LGjk6PmlS1yN6B8dl3xPibgEjcMDAgeu4gejQQzw5ATIrFguUp5OZG8w6RKipne5QyovMVGNWQWrxq1U7UVlmj4iAiS6ushby+IyQdGB4zJmQfWc/1WmQ9Ouj+9A3OW9Ubdld4Yl/jO6k0R5BqDhvz8KtIU26uI/sEJS3pJqxSXCK1WgF8C6/UWx0r4OtSg3uPrB7/EOYYGLR875vzBnF9Gxn95D1a0o8PmWNdVhhNLdIgd+7YcIzhZ6idXfB7d0Tl/EdyzRY+6g7I3oXM8L3b30ly/fXJIwF7/jVsMrZscn7AJst7scnyfzb5ApuM7870K75WtMn2n/6uC/XLEfyF4P5zevYZjvDumMKR6Y/PPx/hywv2S7zYZRnP8JIlkrlrVzmHZYEvMduqsHZ+ZJCEvGBX/P3+ZdS8lUleienmDR6z/3XzHbB9WyNOCzg5ALq94kSHtRa6dIe2upHodS+T5u2u+XL3+b9QSwcI/wAzhKcGAACLFgAAUEsBAhQAFAAICAgACniMQdY3vbkZAAAAFwAAABYAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhX2phdmFzY3JpcHQuanNQSwECFAAUAAgICAAKeIxB/wAzhKcGAACLFgAADAAAAAAAAAAAAAAAAABdAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAACAAIAfgAAAD4HAAAAAA==" showResetIcon = "false" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" /><br /> | ||
| + | |||
| + | {{Definition|P.0 (gleichorientierte nicht kollineare Pfeile}<br />Zwei nicht kollineare Pfeile <math>\vec{AB}</math> und <math>\vec{CD}</math> heißen gleichorientiert, falls <math>AB \|| CD</math> gilt und das Viereck <math>\overline{ABCD}</math> ein überschlagenes Viereck ist.}} | ||
| + | |||
| + | <ggb_applet width="605" height="463" version="4.2" ggbBase64="UEsDBBQACAgIAEp6jEEAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAgIAEp6jEEAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s1Vltb9w2Ev6c/gpCH/rhYGv5Lildp0gcFA3gNsE5Vxzuy4Er0VrVWkmVqPU6yI+/ISntq+P4LTnXyZqiOBxynnlmhlxPf14tSrTUbVfU1UlAQhwgXaV1VlT5SdCbi+M4+PnVD9Nc17metQpd1O1CmZOAhzTYzINeyO3cIjsJlIpnWPD0OEsifsxjHh0nmKrjRCWcklkaRzoNEFp1xcuq/l0tdNeoVJ+nc71QZ3WqjFM5N6Z5OZlcXV2F4+Jh3eaTPJ+Fqy4LEGy86k6C4eElqNuZdMWcOMWYTP7925lXf1xUnVFVqgNkjeqLVz+8mF4VVVZfoasiM/OTQDIwbK6LfA5WSgw2TaxQA6Y2OjXFUncwdavrbDaLJnBiqrLjL/wTKtfmBCgrlkWm25MAh4xILoRMJMVUQCcKUN0WujKDMBkWnYzqpstCX3m99sktyXEC85ZFV8xKfRJcqLIDs4rqogVIYUdtD93OXJd6ptqxv9kQOYJ/IFB80lYX2OlxgI4gR1SKowjjIyEGALYXDpCp69JpxUgk6PNnBIZgdGQb4hsKjZR+CPt3mPmG+ob7RngZ7qdzL8q9DPcynN1i59DfGDq82LF0tJNt20nAPvsBJx9xfGhnvGUnsUZ8RsTu3jUM2X0Tt3/b8KErfTdyDcG+IcNgbH85vOQjLWIPsohsrer58OVFD/gyriixuPuK9FF2rq2kN1lJxResfCS446JEbC0Ka7n/7nOwJLuXnV+E9h4rSv6Y2H/AghH+HgtOJ2Ommw6xh7q5lR3oavSis1mHJS7xIIIEBKaMIE8IRBJoIhugFBGBuIAuiZG0bYSYjUmOGIqRlSMMufQiYvjFXbxKJECXfRn5wEWMI8EQcUmJI0hFyCU2SHKUgYQQSMAkuzqxyzKJuIQOixGHDdqUFtm0wWAe9GFxihhBzM4lEaISSYoimxYJt9lSxnbvoJQiiZG0UyEvQk70+RBmxIhZa4DhTd0Va3DnumzWXnE4FlXTmx3s0kU2Ppp6Tzqr08s3e1hr1ZnxGYSgGG1qni9OOyXxxbRUM13CueHc0gChpSptBDv9F3Vl0EgB6t/lrWrmRdqda2NgVof+VEt1poxe/QLS3bhBt7Sr1FPdp2WRFar6AzhiVViFaF24bV4aCzdnwq+S1nWbnV93QBy0+o9ua0gmhIfJ9g+E0rUfYkSEePsHgO5SZSnPk91JUB2uhyGBdycRv7Rerk1TK702COWtjaetzrvuTV1uXjV1UZlT1Zi+dacwyIKttep1lZfagevyKhxo0stZvTr3qDKv6+N1Az3sdzDLT+uybhFEJBWATj60M986Gbu1tRR2MthJ4NFNRbYeJwl1Eq6d+dZJgd/91gZTyWgmweMyRefyCCj3LBsTr2WNPR/1VWHOxo4p0svBVOIn/N4vZkC4gZG7OslT6ZxO9jg2vdRtpUvPpAqc2dd956m9pueLad/pD8rMX1fZP3UOMflB2bRoQLUX3Ww502mxgIn+/QCeso79F2zVv8103urRxNKdfD20bhRv8/rgtVP1S1sv3lXLj8Cava1OJ6M90y5ti8ayE80gT1/qDf+yolOQ5bPteWB8B1akNuMAkMaCGCDVm3ndusMtxK0NbfRWf9IWVMiVEOg2aEu9gJMtMo6YjttrB712Z2brCVTP/oRUsq4cfnyDGwzfSFJHZ1U2c2XP1QMIpbqGDWzD4vT9Vmf7YIEvnEWQHhrPikZrTyi/X3hoQJ2Lwy2HO/Q7tDoJjmmIbSqwd6cIHj75S5S/M1hjbXju5EL/ds9zQDyP01cQe/P3R4yGsXSAsVDKJwEsrRcLVWWocmeRPwCVug02RVBhyzSkiIXPY9ObcaD3ygYVB+gvvbIR3v4r8G8Z/CX88cPR32AIBYztVCMxUDCO9yqRxXez0DpLG6i8l3C37FwpMUPRcA+/Flmm3bFiP9F0PnmmqjW6gxTpBeBC3ZoP1kdIrxoL9T34fPpfcgjpbhb/G1Aah3zAH/NvwOgzcNseny1ujtH9AaPV7Yy2HFhjq74G/vci9PFN1L2+meiA7zEPWSzkw1mt/6p2OF0smrJIC3O7IxzL9zyhDhzw9nYH7AbA2wcldEL9ac61Tx0BOHxYWo8woyKWnBOORRLRISQSIgVnUSQEpnGSfIuUfze/nN7HL6ff3S/vLy46bVwwRA46yr6913BI4TrEIMa4FJTSJPaHGRyCAzG4DUsuZczxd6vUpz6vvT1w3/JelXr5TCo1DXlMYsolT3gcMxnJEV/Ohb1gJpjBzTX5PxTq09u9c65z+37PPW+8e04P3DO73T3doG3Ef/Zs/CPjKBGSJkwwuP4nzPkHjvXSVhiJsWA8iqKB/olMRCIFlCoJH8rv4i5ys78Au9JG5rvKXhS1u1odXi0vtW7snf599bFVVWf//LJ7p7yvA996B74+cGB6Pwemz8SBkPfYToERgwc53Md2CpJzYRxGSUwJ5LxEEvD6s/bgma5yM99z4OGJL7vdc1W/0G2Rrj2TOYWwhX7AVIQUqM5xQiVhJBbs7m4jDzBgeWCAvp8Bet8ACFYheES5iKjAULjEIyyA3NiC+21lHakc+ITZo3+gpf8y9PYNXuxvkPAQMxFHLAbySXtOetINftQrQ4ZN/vhXX5uf8lIX6Vyj9+7PioVu+yr3I8Hh9g1MD3Z13Tm207rKCn8MAfH34yUC/ZibnxD+ZvG/Vct8EsAu6IVtN+eUr6NGd1ADyVznwFkNJ7FP5qHw0SeAr3xm8E22vwF0X8kPf5R/9T9QSwcIC3K+lxsIAABDIAAAUEsBAhQAFAAICAgASnqMQdY3vbkZAAAAFwAAABYAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhX2phdmFzY3JpcHQuanNQSwECFAAUAAgICABKeoxBC3K+lxsIAABDIAAADAAAAAAAAAAAAAAAAABdAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAACAAIAfgAAALIIAAAAAA==" showResetIcon = "false" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" /><br /> | ||
| + | Sollten <math>\vec{AB}</math> und <math>\vec{CD}</math> auf ein und derselben Geraden liegen, wählen wir zwei Punkte <math>C', D'</math> derart, dass <math>\overline{CDD'C'}</math> ein Parallelogramm ist und vergleichen <math>\vec{AB}</math> mit <math>\vec{C'D'}</math>. <math>\vec{AB}</math> und <math>\vec{CD}</math> sind dann gleichorientiert, falls <math>\vec{AB}</math> und <math>\vec{C'D'}</math> gleichorientiert sind. | ||
| + | {{Definition|P.1 (parallelgleich)<br />Zwei Pfeile <math>\vec{AB}</math> und <math>\vec{CD}</math> heißen parallelgleich, wenn <br /> | ||
| + | # <math>|AB|=|CD|</math> | ||
| + | # <math>AB \|| CD</math> | ||
| + | # <math>\vec{AB}</math> und <math>\vec{CD}</math> sind gleichorientiert.}} | ||
| + | ==Eigenschaften== | ||
| + | ===Satz P.1=== | ||
| + | :Die Relation parallelgleich ist eine ÄR auf der Menge der Pfeile des Raumes bzw. der Ebene.<br /><br /> | ||
| + | <u>Zu zeigen:</u><br /> | ||
| + | a) Reflexivität: <math>\vec{a} \sim \vec{a}</math><br /> | ||
| + | b) Symmetrie: <math>\vec{a} \sim \vec{b} \Rightarrow \vec{b} \sim \vec{a}</math><br /> | ||
| + | c) Transitivität: <math>\vec{a} \sim \vec{b} \wedge \vec{b} \sim \vec{c}\Rightarrow \vec{a} \sim \vec{c}</math><br /><br /> | ||
| + | --[[Benutzer:Jessy*|Jessy*]] 17:08, 11. Dez. 2012 (CET) | ||
| + | ==Definition Pfeilklasse== | ||
| + | {{Definition|P.2 (Pfeilklasse) <br />Eine Pfeilklasse des Raumes bzw. der Ebene ist eine Äquivalenzklasse nach der Relation ''parallelgleich'' auf der menge der Pfeile des Raumes bzw. der Ebene.}} | ||
| + | =Addition von Pfeilklassen= | ||
| + | ==Definition der Addition von Pfeilklassen== | ||
| + | {{Definition|P.3 (Addition auf der Menge der Pfeilklassen)<br />Es seien <math>\vec{u}</math> und <math>\vec{v}</math> zwei Pfeilklassen. Es sei <math>\vec{AB}</math> ein Repräsentant der Pfeilklasse <math>\vec{u}</math>. Aus der Pfeilklasse <math>\vec{v}</math> wählen wir als Repräsentanten den Pfeil, der <math>B</math> als Anfangspunkt hat: <math>\vec{BC} \in \vec{v}</math>. Die Summe <math>\vec{u}+\vec{v}</math> ist die Pfeilklasse, zu der der Pfeil <math>\vec{AC}</math> gehört.<br /><br />}} | ||
| + | Ich habe versucht die Definition zu vervollständigen, stimmt das so? --[[Benutzer:Jessy*|Jessy*]] 17:20, 11. Dez. 2012 (CET)<br /><br /> | ||
| + | <math>\vec{AB}</math> und <math>\vec{BN}</math> jeweils ein Repäsentant von <math>\vec{u}</math> und einer von <math>\vec{v}</math>. Es gilt:<br /><br /> | ||
| + | <math>\vec{AB} + \vec{BN} = \vec{AN}</math><br /><br /> | ||
| + | <math>\vec{AN}</math> ist ein Repräsentant der Pfeilklasse <math>\vec{w}</math> | ||
| + | <u>Kommentar --[[Benutzer:*m.g.*|*m.g.*]] 15:35, 12. Dez. 2012 (CET):</u><br /> | ||
| + | Das passte so schon ganz gut. Ich hab versucht, die Definition ein wenig lesbarer zu gestalten. Ob mir das gelungen ist, bleibt abzuwarten. | ||
| + | Es bleibt zu zeigen: | ||
| + | Satz:(Wohldefiniertheit der Pfeilklassenaddition)<br /> | ||
| + | ::Die Addition von Pfeilklassen ist repräsentantenunabhängig. | ||
<!--- hier drunter nichts eintragen ---> | <!--- hier drunter nichts eintragen ---> | ||
[[Kategorie:Linalg]] | [[Kategorie:Linalg]] | ||
Aktuelle Version vom 12. Dezember 2012, 15:36 Uhr
PfeileProbleme?(Unter einem Pfeil versteht man eine gerichtete Strecke. Wir werden den Begriff intuitiv gebrauchen.)
Offenbar ist es so, dass Ihnen die intuitive Verwendung des Begriffs Pfeil nicht ganz geheuer ist. Ich kann das verstehen.
Hier eine genauere Erläuterung: StreckenStrecken kennen wir aus der Einführung in die Geometrie: Definition Strecke Für Strecken gilt: Eine Strecke hat damit keinen Anfangspunkt. Keiner der beiden Punkte PfeilePfeile sind zunächst dasselbe wie Strecken: Eine Menge von Punkten, die zwischen zwei Punkten Definition Pfeil PfeilklassenDefinition parallelgleich
Definition P.0 (gleichorientierte nicht kollineare Pfeile}
Sollten Definition P.1 (parallelgleich)
EigenschaftenSatz P.1
Zu zeigen: Definition PfeilklasseDefinition P.2 (Pfeilklasse) Addition von PfeilklassenDefinition der Addition von PfeilklassenDefinition P.3 (Addition auf der Menge der Pfeilklassen) Ich habe versucht die Definition zu vervollständigen, stimmt das so? --Jessy* 17:20, 11. Dez. 2012 (CET) Kommentar --*m.g.* 15:35, 12. Dez. 2012 (CET):
Satz:(Wohldefiniertheit der Pfeilklassenaddition)
|
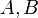 seien zwei verschiedene Punkte.
seien zwei verschiedene Punkte. 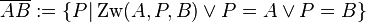
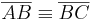 .
.
 und
und  ist dem anderen vorziehen. Beide heißen Endpunkte der Strecke
ist dem anderen vorziehen. Beide heißen Endpunkte der Strecke  .
.
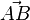
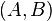 .
. 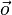 . Zwei Pfeile
. Zwei Pfeile 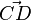 haben einen Punkt gemeinsam falls ihre Punktmengen einen Punkt gemeinsam haben.
haben einen Punkt gemeinsam falls ihre Punktmengen einen Punkt gemeinsam haben.
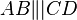 gilt und das Viereck
gilt und das Viereck  ein überschlagenes Viereck ist.
ein überschlagenes Viereck ist.
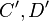 derart, dass
derart, dass 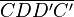 ein Parallelogramm ist und vergleichen
ein Parallelogramm ist und vergleichen 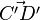 .
. 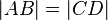
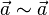
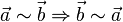
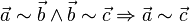
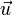 und
und 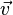 zwei Pfeilklassen. Es sei
zwei Pfeilklassen. Es sei 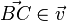 . Die Summe
. Die Summe 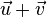 ist die Pfeilklasse, zu der der Pfeil
ist die Pfeilklasse, zu der der Pfeil 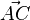 gehört.
gehört.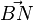 jeweils ein Repäsentant von
jeweils ein Repäsentant von 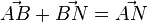
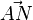 ist ein Repräsentant der Pfeilklasse
ist ein Repräsentant der Pfeilklasse