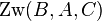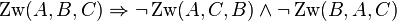Lösung von Aufgabe 6.1 S (WS 12 13): Unterschied zwischen den Versionen
Caro44 (Diskussion | Beiträge) (→Die Beweisführung) |
|||
| (22 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | ==== | + | <div style="margin:0; margin-right:4px; border:1px solid #27408B; padding: 1em 1em 1em 1em; background-color:#FFFF99; align:left;"> |
| + | {|width=90%| style="background-color:#FFFF99; padding:1em" | ||
| + | | valign="top" | | ||
| − | [[ | + | |
| + | ==Aufgabe 6.1== | ||
| + | <u>'''Satz:'''</u> | ||
| + | ::Es seien <math>A,B</math> und <math>C</math> drei paarweise verschiedene Punkte.<br /> | ||
| + | ::Wenn der Punkt <math>B</math> zwischen den Punkten <math>A</math> und <math>C</math> liegt, dann liegt weder <math>A</math> zwischen <math>B</math> und <math>C</math> noch <math>C</math> zwischen <math>A</math> und <math>B</math>. | ||
| + | Beweisen Sie diesen Satz. | ||
| + | |||
| + | <br /> | ||
| + | === Lösung 6.1 von User Hazel12 === | ||
| + | |||
| + | [[Bild:6-1 lösung.jpg|400px]] | ||
| + | ===Bemerkungen Sissy66=== | ||
| + | Ich denke, dass die Voraussetzung ist, dass die 3 Punkte paarweise verschieden sind, also: | ||
| + | |||
| + | Vor: A,B,C sind paarweise verschieden | ||
| + | Beh: Zw(A,B,C) | ||
| + | Ann: Zw(A,B,C) und (oBdA.) Zw(B,A,C) | ||
| + | |||
| + | Wenn man doch oBdA. hinschreibt, muss man den zweiten Teil des Beweises nicht mehr machen, oder?--[[Benutzer:Sissy66|Sissy66]] 14:23, 2. Dez. 2012 (CET) | ||
| + | ===m.g.=== | ||
| + | ====@Sissy66==== | ||
| + | *Eine Implikation kann mehrere Voraussetzungen haben. Im speziellen Fall wäre eine Voraussetzung, dass die drei Punkte paarweise verschieden sind , was noch...?--[[Benutzer:*m.g.*|*m.g.*]] 13:29, 3. Dez. 2012 (CET) | ||
| + | *o.B.d.A. passt nicht ganz, wenn die Aufgabe so formuliert ist, wie sie hier formuliert wurde. Siehe Bemerkungen zu Hazel. | ||
| + | *Formulieren Sie die Aufgabe so, dass o.B.d.A. korrekt wäre.--[[Benutzer:*m.g.*|*m.g.*]] 16:26, 3. Dez. 2012 (CET) | ||
| + | |||
| + | ====@Hazel12==== | ||
| + | =====Die Implikation===== | ||
| + | |||
| + | Wir setzen voraus, dass für die Punkte <math>A \not= B \not= C \not=A </math> gilt. | ||
| + | |||
| + | *Formulierung der Implikation in der Aufgabe:<br /> | ||
| + | ::<math>\operatorname{Zw}(A,B,C) \Rightarrow </math> weder <math>\operatorname{Zw}(A,C,B)</math> noch <math>\operatorname{Zw}(B,A,C)</math> | ||
| + | *Ihre Formulierung der Implikation: | ||
| + | ::<math>\operatorname{Zw}(A,B,C) \Rightarrow \neg \operatorname{Zw}(A,C,B) \wedge \neg \operatorname{Zw}(B,A,C)</math> | ||
| + | |||
| + | *Das mathematische ''und'' | ||
| + | <ggb_applet width="228" height="224" version="4.0" ggbBase64="UEsDBBQACAAIAIhbUUEAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAAIAIhbUUEAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s3Vjrbts2FP7dPsWBUOyXY5O6O7NbJMGyFki7os6KYtgfSmJsLrLoSpQvQx9gb7L32pPskJRkOc6CbB3aYUVd3r5z5blQnbzYLnNY87ISspg6dEgc4EUqM1HMp06tbk5i58Xzp5M5l3OelAxuZLlkaur4GimyqcPTJEzH6fgkjdLgxA8JP2EZYSecJVnC4njsRYkDsK3EaSHfsCWvVizls3TBl+xKpkwZwQulVqej0WazGbaihrKcj+bzZLitMgdQzaKaOs3kFNkdEG08A3cJoaMPr68s+xNRVIoVKXdAm1CL50+fTDaiyOQGNiJTi6nj+r4DCy7mC7TJ80MHRhq0QoeseKrEmldI2lsam9Vy5RgYK/T5EzuDvDPHgUysRcbLqUOG4ziKiD+mMfHcKA7HDshS8EI1WNrIHLXcJmvBN5atnhmJCFqLSiQ5nzo3LK/QJFHclOjObl2pXc4TVnYbe3XowMNz8SuCA4JT6wPcJ2SgfyH+fEKsIj2p6BslZW6YEvj0CVziEhjogdrBxSEM7RGxe8Szg2sH3w6BxfiW3LdQ32J8i/G9npGqrP+mja2Frhs/3kL3s/zaedX16bFMN7hfJg0fEGrtfoydNCB7mSjK/DW/I4neQ2belWjXnycw9L+IiZNRmyqTJk6hWmhsEz2KLysdud4YgrEOQAoBRmkYYbwFQMc4RC5gXAINwA9wSWMI9RiBF+GBDx7EoHHUAxOmQYz/+JFhFkKAzPRuhNkBFAX5EHhATXT7gDENJkMwW1wPEUEAARJp8dTVLLwQ/BBXXgw+6qiTI6II9JAQ1yjeBY+Cp4lpBG4IoeZHfZ10YaxVR5YuhARCqhlifmFu2bxCfAyetqYta6JY1apxUeP1dJm17lJy1W0jHAvSvuzZAnVQFZ9McpbwHBvFTF8lwJrlOiWMpBtZKOiSw+7NS7ZaiLSacaWQqoJf2JpdMcW3l4iuWtkGm8qieltKdSHzellUAKnMSasozmlv7u6NkbnXO/D7B0HvIOzNo3vlSjyBuuIoX5ZVC2dZ9koj9rUBXflDke/OS85uV1IcmjEZmZ4z4XWai0yw4j1Gq5ai/QJtCzIVuW1BURy0isgym+0qDGHY/sRLidWYuEPS+4NpsrMn3tg07ipluSnxBzCD6x1Z/nzdXQPb8s7CeSmy/vxVdS7zrLPXmHjBVqouzQMBNS+14mfFPOcmDExJxe6b3iZyO7NZ7Fle17sVrhr5ydy4FjD/3SBAQDMmdjQYrViHIgZDDIK0ASWy7pyOXYMwY2JHg8IItao1htLWSkpaMaIyVYs4B+XDhPfU2TpQF0Jd2RWmiUhvG1OpJXhTLxNeHgZwx5Tey3T3D5hORncCaVKtMO6yasG5uje0TCtsQ4uOQ6saEt1c8Dyf9aER6b2DYgvssbd52LbMloY+hPM6HCUPAv090I0aIM91nZEFwGKWljLPze2se/PUMDDqlKbrNrfNdrLWpQddeIlv1Tpn570mo7e/N7ff23hp2d7Fvb9/+xzFVbx8i6+1/ODAmvQSLeSHFO9QhNmFbpvludzMsJgKln+XCSW7xmtOrrGbXYtVl5b8Y41073AQJW8T9MileKeX5nkOzTP9NcOK7g3CARuQUzIgehwkg+iUDvxmTr1BOjihYURpGNNTf0AN2MUXTDPZU7kNJ89S49iB6AE7Nwg1J9LIve/QcvItd+Q0btZxs44axuNmbNftudeMdk3N2jVa+h0vQ2Mz5yhTJre8xAtsaj4WwlrWlW1hvSzO8IKWuLQHTUFhutj9iNlrdzM+L3mb9bn5dLHlxpySfjk/2jasLku5fFWsr7GS3lFgMmq1nFRpKVa6XkOCD6Vbvo/gTFQM31lZn043KYwRm0JKKF1XMLRqtdCBthzOh0iHnRd3dX/aoncq/QXYlqczLEK4O3W++VhL9e2ZHQxrzMwlfryAMtUcm7dyelQmJDHkQSa/YAbvH3cW0XMtAv6itmMKrBZMfzmRLqcxd/p+M+xey6zvTSyPVrV7Lbo4tOj8cRZd/HcsOlAywfrAWbH3vGv0RNK6YdCrEP+28g+07j26a+KPMxVTod6KXLByd6j/431wceSDnnn/IycchfZ50IT2mQt//PY7oCPgOK7vugupvo67yNFj7wu7yz+oBM/O4OecFRmcP3tcTUD6r1gT8COuumLX/MPdNDdfXPguETf7t4d5fpPmW/ueojLq9wnzvdL839vzPwFQSwcIqnZ5BoMGAAAYFAAAUEsBAhQAFAAIAAgAiFtRQdY3vbkZAAAAFwAAABYAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhX2phdmFzY3JpcHQuanNQSwECFAAUAAgACACIW1FBqnZ5BoMGAAAYFAAADAAAAAAAAAAAAAAAAABdAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAACAAIAfgAAABoHAAAAAA==" showResetIcon = "false" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "true" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "false" /><br /> | ||
| + | *Fazit: Sie haben das ''weder noch'' gut umgesetzt | ||
| + | |||
| + | ====Die Beweisführung==== | ||
| + | korrekt | ||
| + | |||
| + | |||
| + | Es wäre ausreichend, den Beweis nur für einen Fall zu formulieren. Fall 2: analog. | ||
| + | |||
| + | Warum wäre o.B.D.A, in unserem Fall nicht korrekt? | ||
| + | |||
| + | |||
| + | |||
| + | '''Frage:''' Können wir davon ausgehen, dass die 3 Punkte (A;B;C) kollinear sind?<br /> | ||
| + | Und stimmt die Begründung "Def. Zwischenrelation"? Müsste die Begründung nicht "Umkehrung der Zwischenrelation" heißen? <br />--[[Benutzer:Caro44|Caro44]] 17:42, 5. Dez. 2012 (CET) | ||
| + | |||
| + | <!--- Was hier drunter steht muss stehen bleiben ---> | ||
| + | |} | ||
| + | </div> | ||
| + | |||
| + | [[Kategorie:Einführung_S]] | ||
Aktuelle Version vom 5. Dezember 2012, 17:42 Uhr
|
Aufgabe 6.1Satz:
Beweisen Sie diesen Satz.
Lösung 6.1 von User Hazel12Bemerkungen Sissy66Ich denke, dass die Voraussetzung ist, dass die 3 Punkte paarweise verschieden sind, also: Vor: A,B,C sind paarweise verschieden Beh: Zw(A,B,C) Ann: Zw(A,B,C) und (oBdA.) Zw(B,A,C) Wenn man doch oBdA. hinschreibt, muss man den zweiten Teil des Beweises nicht mehr machen, oder?--Sissy66 14:23, 2. Dez. 2012 (CET) m.g.@Sissy66
@Hazel12Die ImplikationWir setzen voraus, dass für die Punkte
Die Beweisführungkorrekt
Warum wäre o.B.D.A, in unserem Fall nicht korrekt?
Frage: Können wir davon ausgehen, dass die 3 Punkte (A;B;C) kollinear sind? |
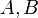 und
und  drei paarweise verschiedene Punkte.
drei paarweise verschiedene Punkte. zwischen den Punkten
zwischen den Punkten  und
und 
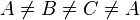 gilt.
gilt.
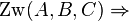 weder
weder 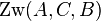 noch
noch