Lösung von Zusatzaufgabe 6.2P (WS 12 13): Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(Die Seite wurde neu angelegt: „Beweisen Sie: Es sei <math> \operatorname{koll} \left( A, B, C \right) </math> mit <math>\ A, B, C</math> sind paarweise verschieden.<br /> Dann gilt genau eine d…“)
 
 
(7 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt)
Zeile 1: Zeile 1:
 
Beweisen Sie: Es sei <math> \operatorname{koll} \left( A, B, C \right) </math> mit <math>\ A, B, C</math> sind paarweise verschieden.<br /> Dann gilt genau eine der folgenden Zwischenrelationen: <math> \operatorname{Zw} \left( A, B, C \right) </math> oder <math> \operatorname{Zw} \left( A, C, B \right) </math> oder <math> \operatorname{Zw} \left( B, A, C \right) </math>.
 
Beweisen Sie: Es sei <math> \operatorname{koll} \left( A, B, C \right) </math> mit <math>\ A, B, C</math> sind paarweise verschieden.<br /> Dann gilt genau eine der folgenden Zwischenrelationen: <math> \operatorname{Zw} \left( A, B, C \right) </math> oder <math> \operatorname{Zw} \left( A, C, B \right) </math> oder <math> \operatorname{Zw} \left( B, A, C \right) </math>.
  
 +
Als Hilfe schon mal eine Tabelle. Für die Findung der Lösung darf auch nur angefangen werden. Ist es sinnvoll den Beweis direkt oder indirekt durch Widerspruch zu beweisen? Welche Definitionen sind vermutlich hilfreich? --[[Benutzer:Tutorin Anne|Tutorin Anne]] 12:36, 10. Dez. 2012 (CET)<br />
 +
<br />
 +
Beweis durch Kontraposition:<br />
 +
Note: <math>\neg (Zw (A,B,C)\vee Zw (A,C,B)\vee Zw (B,A,C)) \Leftrightarrow \neg Zw (A,B,C) \wedge \neg Zw (A,C,B) \wedge \neg Zw (B,A,C)</math><br />
 +
{| class="wikitable"
 +
| Voraussetzung || <math>\neg Zw (A,B,C) \wedge \neg Zw (A,C,B) \wedge \neg Zw (B,A,C)</math>
 +
|-
 +
| Behauptung || <math>\neg koll (A,B,C)</math>
 +
|}
 +
<br />
 +
Fall 1: <math>\neg Zw (A,B,C)</math>  (Vor1)<br />
 +
 +
Fall 2: <math>\neg Zw (A,C,B)</math>  (Vor2)<br />
 +
 +
Fall 3: <math>\neg Zw (B,A,C)</math>  (Vor3)<br />
 +
 +
Zu Fall 1:<br />
 +
 +
{| class="wikitable"
 +
!Beweisschritt!!Begründung
 +
|-
 +
| 1 |1 |AB| + |BC| > |AC| v |AB| + |BC| < |AC| || Vor1; Def. Zw
 +
|-
 +
| 2 Es existiert ein Dreieck ABC || 1.); Dreiecksungleichung
 +
|-
 +
| 3 <math>\neg koll (A,B,C)</math> || 2.); Def. koll
 +
|}
 +
<br />
 +
Fall 2 und 3 analog zu Fall 1. <br />
 +
q.e.d.<br />
 +
 +
* Tolle Idee. Aber auch hier muss man genau hinsehen:<br />
 +
Deine Note (= Notiz?) ist richtig, wie auch die Kontraposition, die du in Voraussetzung und Behauptung geteilt hast.
 +
Aber dann Vorsicht: Zuerst sehe ich es als problematisch eine Voraussetzung in Fälle zu unterteilen. Es geht ja um die gesamte Aussage.<br />
 +
Zweitens, der Teilbeweis für Fall 1 stimmt so nicht. Schritt 2 kannst du nicht folgern. Denn dies steht so nicht in der Dreiecksungleichung drin.Es kann aus |AB| + |BC| > |AC| immer noch folgen, dass koll (A,B,C) ist z.B. wenn Zw (A,C,B)gilt (Mache dir dazu eine Skizze).--[[Benutzer:Tutorin Anne|Tutorin Anne]] 12:20, 20. Jan. 2013 (CET)<br />
 +
 +
Naja, die Aussage ist ja nur dann richtig, wenn die 3 Fälle jeweils zu <math>\neg koll (A,B,C)</math> führen. Ich kann also auch sagen: <math>(\neg Zw (A,B,C)\Rightarrow \neg koll (A,B,C)) \wedge (\neg Zw (A,C,B) \Rightarrow \neg koll (A,B,C))\wedge (\neg Zw (B,A,C)\Rightarrow \neg koll (A,B,C))</math><br />
 +
Daher hab ich die 3 Fälle. ;)--[[Benutzer:Unicycle|Unicycle]] 17:15, 20. Jan. 2013 (CET)<br />
 +
* Super erklärt, da hast du Recht.--[[Benutzer:Tutorin Anne|Tutorin Anne]] 13:18, 21. Jan. 2013 (CET)
 +
Aber es gilt doch nach Vor1: <math>\neg Zw (A,B,C)</math> und ''deswegen können A, B und C nicht kollinear sein'', denn dann würde Zw (A,B,C) ja gelten.<br />
 +
 +
Wenn ich sage: |AB| + |BC| > |AC| dann existiert ein Dreieck A, B, C, wenn ich sage: |AB| + |BC| >/= |AC|, dann könnten sie auch kolliniear sein, aber das können sie nicht, wegen Voraussetzung 1.--[[Benutzer:Unicycle|Unicycle]] 17:15, 20. Jan. 2013 (CET)<br />
 +
* Das stimmt nicht! Nur weil eine Zwischenrelation nicht gilt, heißt das nicht, dass die Punkte nicht kollinear sein können. Immerhin kann ja eine andere Zwischenrelation gelten.--[[Benutzer:Tutorin Anne|Tutorin Anne]] 13:18, 21. Jan. 2013 (CET)<br /><br />
 +
Tipp: Der Beweis lässt sich am einfachsten indirekt beweisen. Man nimmt an, dass zwei Zwischenrelationen gleichzeitig gelten (alos indrekter Beweis mit Widerspruch).<br />
 +
Hier nochmal die Tabelle:--[[Benutzer:Tutorin Anne|Tutorin Anne]] 13:18, 21. Jan. 2013 (CET)<br />
 +
{| class="wikitable"
 +
|  Voraussetzung || (V. hier eintragen)
 +
|-
 +
| Behauptung || (Beh. hier eintragen)
 +
|-
 +
| Annahme || (hier eintragen)
 +
|}
 +
<br />
 +
 +
{| class="wikitable"
 +
!Nr. !!Beweisschritt!!Begründung
 +
|-
 +
| 1 ||(Schritt 1 hier)|| (Begründung 1)
 +
|-
 +
| 2 || (Schritt 2) || (Begründung 2)
 +
|-
 +
| 3 || (Schritt) || (Begründung)
 +
|-
 +
| 4 || (Schritt) || (Begründung)
 +
|}
  
  
 
[[Kategorie:Einführung_P]]
 
[[Kategorie:Einführung_P]]

Aktuelle Version vom 21. Januar 2013, 13:18 Uhr

Beweisen Sie: Es sei \operatorname{koll} \left( A, B, C \right) mit \ A, B, C sind paarweise verschieden.
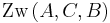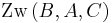Dann gilt genau eine der folgenden Zwischenrelationen: \operatorname{Zw} \left( A, B, C \right) oder \operatorname{Zw} \left( A, C, B \right) oder \operatorname{Zw} \left( B, A, C \right) .

Als Hilfe schon mal eine Tabelle. Für die Findung der Lösung darf auch nur angefangen werden. Ist es sinnvoll den Beweis direkt oder indirekt durch Widerspruch zu beweisen? Welche Definitionen sind vermutlich hilfreich? --Tutorin Anne 12:36, 10. Dez. 2012 (CET)

Beweis durch Kontraposition:
Note: 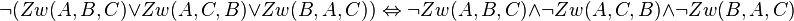\neg (Zw (A,B,C)\vee Zw (A,C,B)\vee Zw (B,A,C)) \Leftrightarrow \neg Zw (A,B,C) \wedge \neg Zw (A,C,B) \wedge \neg Zw (B,A,C)

Voraussetzung 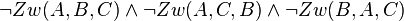\neg Zw (A,B,C) \wedge \neg Zw (A,C,B) \wedge \neg Zw (B,A,C)
Behauptung 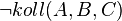\neg koll (A,B,C)


Fall 1: 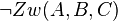\neg Zw (A,B,C) (Vor1)

Fall 2: 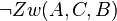\neg Zw (A,C,B) (Vor2)

Fall 3: 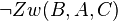\neg Zw (B,A,C) (Vor3)

Zu Fall 1:

Beweisschritt Begründung
1 |AB| + |BC| > |AC| v |AB| + |BC| < |AC| Vor1; Def. Zw
2 Es existiert ein Dreieck ABC 1.); Dreiecksungleichung
3 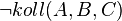\neg koll (A,B,C) 2.); Def. koll


Fall 2 und 3 analog zu Fall 1.
q.e.d.

  • Tolle Idee. Aber auch hier muss man genau hinsehen:

Deine Note (= Notiz?) ist richtig, wie auch die Kontraposition, die du in Voraussetzung und Behauptung geteilt hast. Aber dann Vorsicht: Zuerst sehe ich es als problematisch eine Voraussetzung in Fälle zu unterteilen. Es geht ja um die gesamte Aussage.
Zweitens, der Teilbeweis für Fall 1 stimmt so nicht. Schritt 2 kannst du nicht folgern. Denn dies steht so nicht in der Dreiecksungleichung drin.Es kann aus |AB| + |BC| > |AC| immer noch folgen, dass koll (A,B,C) ist z.B. wenn Zw (A,C,B)gilt (Mache dir dazu eine Skizze).--Tutorin Anne 12:20, 20. Jan. 2013 (CET)

Naja, die Aussage ist ja nur dann richtig, wenn die 3 Fälle jeweils zu 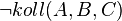\neg koll (A,B,C) führen. Ich kann also auch sagen: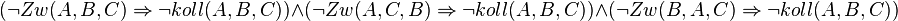 (\neg Zw (A,B,C)\Rightarrow \neg koll (A,B,C)) \wedge (\neg Zw (A,C,B) \Rightarrow \neg koll (A,B,C))\wedge (\neg Zw (B,A,C)\Rightarrow \neg koll (A,B,C))
Daher hab ich die 3 Fälle. ;)--Unicycle 17:15, 20. Jan. 2013 (CET)

  • Super erklärt, da hast du Recht.--Tutorin Anne 13:18, 21. Jan. 2013 (CET)

Aber es gilt doch nach Vor1: 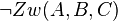\neg Zw (A,B,C) und deswegen können A, B und C nicht kollinear sein, denn dann würde Zw (A,B,C) ja gelten.

Wenn ich sage: |AB| + |BC| > |AC| dann existiert ein Dreieck A, B, C, wenn ich sage: |AB| + |BC| >/= |AC|, dann könnten sie auch kolliniear sein, aber das können sie nicht, wegen Voraussetzung 1.--Unicycle 17:15, 20. Jan. 2013 (CET)

  • Das stimmt nicht! Nur weil eine Zwischenrelation nicht gilt, heißt das nicht, dass die Punkte nicht kollinear sein können. Immerhin kann ja eine andere Zwischenrelation gelten.--Tutorin Anne 13:18, 21. Jan. 2013 (CET)

Tipp: Der Beweis lässt sich am einfachsten indirekt beweisen. Man nimmt an, dass zwei Zwischenrelationen gleichzeitig gelten (alos indrekter Beweis mit Widerspruch).
Hier nochmal die Tabelle:--Tutorin Anne 13:18, 21. Jan. 2013 (CET)

Voraussetzung (V. hier eintragen)
Behauptung (Beh. hier eintragen)
Annahme (hier eintragen)


Nr. Beweisschritt Begründung
1 (Schritt 1 hier) (Begründung 1)
2 (Schritt 2) (Begründung 2)
3 (Schritt) (Begründung)
4 (Schritt) (Begründung)
Von „http://geometrie.zum.de/index.php?title=Lösung_von_Zusatzaufgabe_6.2P_(WS_12_13)&oldid=20502“