Strahlen bzw. Halbgeraden WS 12 13: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „= Halbgeraden bzw. Strahlen = ===== So ist es gemeint ===== Hinweis: Klicken Sie auf das Symbol rechts oben (neu laden), damit alles richtig angezeigt wird.<br />…“) |
*m.g.* (Diskussion | Beiträge) (→Definition II.5: (Halbgerade, bzw. Strahl)) |
||
| (17 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| + | <div style="margin:0; margin-right:4px; border:1px solid #27408B; padding: 1em 1em 1em 1em; background-color:#FFFF99; align:left;"> | ||
| + | {|width=90%| style="background-color:#FFFF99; padding:1em" | ||
| + | | valign="top" | | ||
| + | |||
| + | <!--- ------------------------------------------------------------------------------------------ ---> | ||
| + | |||
| + | |||
| + | |||
= Halbgeraden bzw. Strahlen = | = Halbgeraden bzw. Strahlen = | ||
| − | ===== | + | ===== Geogebra-App ===== |
| − | + | ||
| − | + | ||
| + | *Verschieben Sie <math>P</math> auf <math>AB</math> | ||
| + | *Manipulieren Sie <math>A</math> und <math>B</math> für eine andere Lage der Geraden <math>AB</math> | ||
| − | <ggb_applet width=" | + | |
| + | <ggb_applet width="606" height="426" version="4.2" ggbBase64="UEsDBBQACAgIALBuiEEAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAgIALBuiEEAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s3VrrbuPGFf69eYoBYRQtYslzJ7mVN5DtBl3AmxixWwSLoosROZYYUyRDUpbtbv6nT9G/fa48Sc/MkLIutleylIW39srDIc+cOed85zbU9r65GafoWpdVkmeHHuliD+ksyuMkGx56k/qyE3jfvPmqN9T5UA9KhS7zcqzqQ493qXe/DmZdbtYm8aF3ScKAR0R2VMBlhwsZdQIyUJ2ASUZVIAMVxB5CN1XyOsu/U2NdFSrS59FIj9VpHqnashzVdfH64GA6nXbbzbt5OTwYDgfdmwoYgOBZdeg1F6+B3cKiKbPkFGNy8OO7U8e+k2RVrbJIe8goNUnefPWqN02yOJ+iaRLXo0NPMuahkU6GI9BSSJgcGKICVC10VCfXuoKlc1Orcz0uPEumMvP8lbtC6UwdD8XJdRLr8tDDXUZEKIQvJQmpb/bLy0RndUNKmi0PWma960RPHVdzZTfkOPQBgKRKBqkGm6u0AqWS7LIEg4I85QSmVX2b6oEq2/m9OGQffoEgudOGFyDnrAAT6u9zSvZ9jPeFwE6W+Y09VOd5arliJEL08SOimGK0bwbiBgqDlO4RdvcwcwN1A3eDcDTcLeeOlDsa7mg4e0LPZn6vaHNjQdNWTzavJwH9zEfCxxpgSc9gTk9ilPiIiJHeDgwZuYmV3wy8mUo39e1AsBtI8zAwf6y95JYasWdpROZ2df7w+KYr/tLuKLFcf0e6lZ4zLelDWlLxiJZbGrfdlIi5TWEv+89+VrZkG+n5qGk32FHybWL/GRv6+HNs2DtoM12viT1UjQxt4661Hlcm67DQJh5EkIDAlD7kCYFICINvApQiIhAXMCUBkmb0ETMxyRFDATJ0hCGbXkQAf7iNV4kE8DI3fRe4iHEkGCI2KXEEqQjZxAZJjjKgEAIJWGR2J2ZbJhGXMGEB4iCgSWm+SRsM1sEcNqeIEcTMWuIjKpGkyDdpkXCTLWVgZAemFEmMpFkKeRFyosuHsCJAzGgDHl7kVTIz7kinxQwVa8ckKyb1gu2icdxe1vkSdZxHV0dLttaqqttrIIJidF/xXHFaKIiveqka6BS6hnPjBghdq9REsOV/mWc1al2AunvDUhWjJKrOdV3Dqgr9pK7Vqar1zbdAXbUC2q1tne7pSZQmcaKyv4OPGBaGIZqVbZOX2rLNwsDtEuV5GZ/fVuA46Oa9LnMQICDdcP4HDHjrHlEWdvH8j8lAkTIuz8PFRVAdbptHAi8uahTU1zPV1I2eKYSGpe2R7idvq6M8vb9V5ElWH6uinpS2BwMZSqNVPxum2hrX5lVoZ6KrQX5z7qzKHK+L2wJm2EkwGB7naV4iiEgqBBA048CNlsaINqPClgZbCtzClMSz59CtWAo7DtxoqQB3J1qjKmnVJLjdJqlsHgHmzsvaxGu8xnRHkyypT9tJnURXjarELfhuMh6AwzUeuciT7Ipn72DJx3pXusx06jwpAzAn+aRyrj1zz1e9SaXPVD3qZ/EPeggxeaZMWqyBtSO9FznWUTKGhe5+YzxlgP0biOruxnpY6lbF1Pa9zrT2KZ7365XbltW3ZT5+m11fgNcsido7aPXpVVGZFMY70QDy9JW+9784qRRk+Xh+HShfgRaRyThgyNoY0UNqUo/y0ra2ELfQMaETfaeNTSFVQpybmE31GBpbVFu/tK49w6dvG2YDBMoHP0EmmRUO9/zebPD4QR+13qzSYqRMU93YIFW3IMC8VSy/d3msF5KSygAKqxBkh8I5RaG18ycnL1wUwM6G4Rze1vgVujn0Oticgm7N7gQq8p07QLnzgtHVBOfCpu7uKpwQ7kYSe2+vv9c4ozPeJ8x49OWbkXWJM6M9fu7IikcrVozy8VhlMcps03IKOcu7r5UKG49EihiLOnNN6vaBcqwaBiuAmPQ3s7f6BB5zFngMEPwMOPADvhlIa1XWZXS5rN1ZAslksJzBa6jKV3DurGyZqZuCYi/+msSxti2Hq3A/Z25J5dJqMi7SJErqp+1+Zr130fBqxeJnT1t8MQTOtg6B51j8kQCAVPCsEAhCSYiQVIqQEyJlExCQSeFYDB0H3A8pCXYWH2efiI+TpHlTsgjVmYuR/gpi8QfyNGbZZKzLJJqhYhbYlxsqnTSC8i5lhOHAh0M/F6Dw+qiRbbRZjfj4A91UG7qsDQQgJj4j3Mch5YL79PdW5+hxcNim6rBldViX01D4PmWMU4IF5Vuoo2+KEnKMccdmx/fT/hnIDw+sa6CvEZgUdZCRxJ5AnhbYLV8SmXQlZlxSiKiAhzjk2yDwkMhnR/2ZyNSKzKzIZD2RzfIlkYNuEBA/gJD3MTRRgv6lQ+Supe4vG9pJTdeUur9iaNkNREgE51IGxjm2cY1FTz/XQ3N/XUcfPO3mVcOtVWawfrGGHjhOXJ4H8u8baut26Ld//wfh36PJWqnqs6LeeaSqf7Ko+08XdbBlaurU28wcYLRt+VePPFdaF+as+X12UaqsMl8KLJ51tq3/x5vU/+NVFBePgg83ABBd7jhLxfYQ7aIPDk2G5VLIUFLiS+ZbpCkgypkfQmjR0GcsZM/uAR5H5Qd1+3CIHa9AEz0NTQmcWrtH24cXpMjPGF4d8oCxb01+Y3gJmTtLDbkOOjTCCKFhyALxROCJLyLwTjYJvJP/k8Dr0C5A7YsAUw6AEuZzl2RxlxNOfVPWgpCF1DdvGT9D8DUn0ZPVRm794It3EHz9R2tb+0bRhZ8guyluQixYmzgUaJcsokObUgdT24r6RMCpgUv2osJvtfW60Dc1aVqvP/w8yes/76F/5IUuVZ2Xxhf+9X76C/rj2f7Rfv9PaM+ReKs9WQ18vEWmX0SiTapTdaF/XH4tar8fqKDLvJx9lwQR9a55H+S+N8Be+5qh4QUHoLK2OQ0538HNy46FV0hr4PFhDUT6+4DJZoh82AEmn6O3fJmY0HWipL8xJvQLyYkvEZRFSM7rUo1StNc/+ufXG0CwAwBmQYF++/W/6KUmLt7iIdbEg2+Mx1LimkOkswkiu0hULzQodgnCwfyXYPZb6eZ/pb35H1BLBwhNNi0A4wgAAEQnAABQSwECFAAUAAgICACwbohB1je9uRkAAAAXAAAAFgAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc1BLAQIUABQACAgIALBuiEFNNi0A4wgAAEQnAAAMAAAAAAAAAAAAAAAAAF0AAABnZW9nZWJyYS54bWxQSwUGAAAAAAIAAgB+AAAAegkAAAAA" showResetIcon = "false" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" /> | ||
===== Definition II.5: (Halbgerade, bzw. Strahl) ===== | ===== Definition II.5: (Halbgerade, bzw. Strahl) ===== | ||
| + | (Ergänzen Sie die fehlenden Teile selbst.)<br /> | ||
| + | {{Definition|'''offene Halbgerade <math>AB^+</math>'''<br />Es sei <math>AB</math> eine Gerade. Unter der offenen Halbgeraden <math>AB^+</math> versteht man die Menge aller Punkte <math>P</math> für die gilt: <br />(a) Zw(A,P,B) <br /> oder <br />(b) Zw(A,B,P)<br />Der Punkt <math>A</math> heißt Anfangspunkt von <math>AB^+</math>.}} | ||
| + | {{Definition|'''offene Halbgerade <math>AB^-</math>'''<br />Es sei <math>AB</math> eine Gerade. Unter der offenen Halbgeraden <math>AB^-</math> versteht man die Menge aller Punkte <math>P</math> für die gilt: Zw (P,A,B) <br />Der Punkt <math>A</math> heißt Anfangspunkt von <math>AB^-</math>.}} | ||
| + | {{Definition|'''Halbgeraden <math>AB^+</math> bzw. <math>AB^-</math>'''<br /> Es sei <math>AB</math> eine Gerade. Unter den Halbgeraden <math>AB^+</math> bzw. <math>AB^-</math> versteht man die offenen Halbgeraden <math>AB+</math> bzw. <math>AB^-</math> jeweils vereinigt mit den Punkten A und B. }}<br/> | ||
| + | |||
| + | Bei der offenen Halbgeraden AB+ muss noch der Punkt B dazu! | ||
| + | --[[Benutzer:Caro44|Caro44]] 16:05, 8. Dez. 2012 (CET)<br /> | ||
| + | korrekt --[[Benutzer:*m.g.*|*m.g.*]] 17:56, 15. Dez. 2012 (CET) | ||
| + | |||
| + | <!--- Das, was hier drunter steht muss stehen bleiben, also oberhalb dieses Kommentars Änderungen einfügen ---> | ||
| + | |} | ||
| + | </div> | ||
| + | |||
| + | |||
| + | [[Category:Einführung_S]] | ||
Aktuelle Version vom 15. Dezember 2012, 17:56 Uhr
|
Halbgeraden bzw. StrahlenGeogebra-App
Definition II.5: (Halbgerade, bzw. Strahl)(Ergänzen Sie die fehlenden Teile selbst.) Definition offene Halbgerade Definition offene Halbgerade Definition Halbgeraden Bei der offenen Halbgeraden AB+ muss noch der Punkt B dazu!
--Caro44 16:05, 8. Dez. 2012 (CET) |
 auf
auf 
 und
und  für eine andere Lage der Geraden
für eine andere Lage der Geraden 

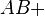 bzw.
bzw. 
