Vektorräume 2012 13: Unterschied zwischen den Versionen
K |
|||
| (6 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| + | <div style="margin:0; margin-right:4px; border:1px solid #27408B; padding: 1em 1em 1em 1em; background-color:#B9D0F0; align:left;"> | ||
| + | {|width=90%| style="background-color:#B9D0F0; padding:1em" | ||
| + | | valign="top" | | ||
| + | <!--- hier drüber nichts eintragen ---> | ||
| + | |||
| + | |||
=Definition des Begriff des Vektorraums= | =Definition des Begriff des Vektorraums= | ||
| Zeile 15: | Zeile 21: | ||
A2: Für beliebige <math>u,v.w \in V</math> gilt <math>(u+v)+w=u+(v+w)</math>. (Assoziativität der Addition) | A2: Für beliebige <math>u,v.w \in V</math> gilt <math>(u+v)+w=u+(v+w)</math>. (Assoziativität der Addition) | ||
| − | A3: Es gibt ein neutrales Element <math>e\in V</math>, mit dem für alle Elemente <math>u\in V</math> gilt: <math>u | + | A3: Es gibt ein neutrales Element <math>e\in V</math>, mit dem für alle Elemente <math>u\in V</math> gilt: <math>u+ e = e+ u = u</math>. (Existenz eines neutralen Elements/Nullvektor) |
| − | + | ||
| − | + | A4: Zu jeden <math>u\in V</math> existiert ein Gegenvektor <math>-u \in V</math> mit<math>u+(-u)=e. </math> | |
S1: Für beliebige <math>v \in V</math> gilt <math>1\cdot u =u</math>. | S1: Für beliebige <math>v \in V</math> gilt <math>1\cdot u =u</math>. | ||
Aktuelle Version vom 12. Dezember 2012, 15:23 Uhr
|
Definition des Begriff des VektorraumsEine nicht leere Menge V zusammen mit einer inneren Verknüpfung
und der äußeren Verknüpfung
heißt reeler Verktorraum, falls folgende Bedingungen erfüllt sind: A1: Für beliebige A2: Für beliebige A3: Es gibt ein neutrales Element A4: Zu jeden S1: Für beliebige S2: Für beliebige S3: Für beliebige S4: Für beliebige Bemerkung:Die Eigenschaften A1-A4 lassen sich zusammenfassen, dass Die Menge aller Pfeilklassen in der Ebene (und die Pfeilklassen des Raumes) mit den Eigenschaften, wie in der Vorlesung gezeigt, bilden einen Vektorraum. (Quelle: Filler: Elementare Lineare Algebra. Spektrum Akademischer Verlag) |
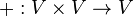 ,
, 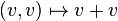
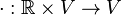 ,
, 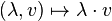
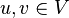 gilt
gilt 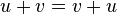 (Kommuntativität der Addition).
(Kommuntativität der Addition).
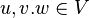 gilt
gilt 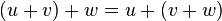 . (Assoziativität der Addition)
. (Assoziativität der Addition)
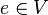 , mit dem für alle Elemente
, mit dem für alle Elemente 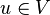 gilt:
gilt: 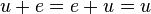 . (Existenz eines neutralen Elements/Nullvektor)
. (Existenz eines neutralen Elements/Nullvektor)
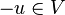 mit
mit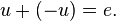
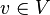 gilt
gilt 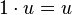 .
.
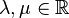 gilt:
gilt: 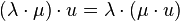 (Assoziativität der Multiplikation von Vektoren mit reelen Zahlen)
(Assoziativität der Multiplikation von Vektoren mit reelen Zahlen)
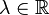 gilt:
gilt: 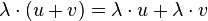 (1.Distributivgesetz)
(1.Distributivgesetz)
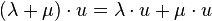 (2.Distributivgesetz)
(2.Distributivgesetz)
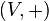 eine Abelsche Gruppe bildet.
eine Abelsche Gruppe bildet.

