Gruppen, abelsche Gruppen 2012 12: Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „=Beispiele für endliche Gruppen= ==Restklassen modulo 4== <math>\mathbb{Z}_4:=\left\{ \overline{0}, \overline{1}, \overline{2}, \overline{3} \right\}</math>“) |
Jessy* (Diskussion | Beiträge) (→Gruppeneigenschaften) |
||
| (55 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| + | <div style="margin:0; margin-right:4px; border:1px solid #27408B; padding: 1em 1em 1em 1em; background-color:#B9D0F0; align:left;"> | ||
| + | {|width=90%| style="background-color:#B9D0F0; padding:1em" | ||
| + | | valign="top" | | ||
| + | <!--- hier drüber nichts eintragen ---> | ||
| + | |||
| + | |||
| + | =Gruppeneigenschaften= | ||
| + | Eine Verknüpfung <math>\odot</math> bzw. einer Operation auf einer Menge M ist eine '''Gruppe''', wenn folgende Eigenschaften erfüllt sind:<br /> | ||
| + | '''1. Abgeschlossenheit:''' die Verknüfung <math>\odot</math> auf der Menge M ist abgeschlossen: Verknüpft man ein Element der Menge mit einem anderen Element der Menge, erhält man wiederum ein Element der Menge<br /> | ||
| + | <math> \quad \quad \forall a,b \in M: a \odot b \in M</math><br /> | ||
| + | '''2. Assoziativität:''' die Verknüfung <math>\odot</math> auf der Menge M ist assoziativ<br /> | ||
| + | <math> \quad \quad \forall a,b,c \in M: (a \odot b) \odot c = a \odot (b \odot c)</math><br /> | ||
| + | '''3. Neutrales Element:''' Innerhalb der Menge M gibt es ein neutrales Element e <br /> | ||
| + | <math> \quad \quad \forall a \in M: e \odot a = a \odot e = a</math><br /> | ||
| + | '''4. Inverse Elemente:''' Für jedes Element aus M gibt es ein Inverses Element <br /> | ||
| + | <math> \quad \quad \forall a \in M: a \odot a^{-1} = e \quad \quad \quad \quad</math> mit <math>a^{-1} \in M</math> und e = neutrales Element<br /><br /> | ||
| + | Erfüllt eine Verknüfung <math>\odot</math> auf der Menge M hingegen nicht alle Punkte, aber mindestnes die <u>Abgeschlossenheit</u> und die <u>Assoziativität</u>, so handelt es sich um eine '''Halbgruppe'''.<br /><br /> | ||
| + | Erfüllt eine Gruppe zusätzlich eine weitere Eigenschaft, nämmlich die Kommutativität, so ist sie eine '''kommutative bzw. abelsche Gruppe'''<br /> | ||
| + | '''5. Kommutativität:''' Die Reihenfolge in welcher die Elemente der Menge M mit <math>\odot</math> Verknüpft werden ist egal<br /> | ||
| + | <math> \quad \quad \forall a,b \in M: a \odot b = b \odot a</math><br /><br /> | ||
| + | --[[Benutzer:Jessy*|Jessy*]] 11:38, 12. Dez. 2012 (CET) | ||
| + | |||
| + | <u>Bemerkung --[[Benutzer:*m.g.*|*m.g.*]] 14:14, 12. Dez. 2012 (CET):</u><br /> | ||
| + | Vielen Dank für Ihre Bemühungen. bezüglich der Abgeschlossenheit muss ein wenig korrigiert werden:<br /> | ||
| + | Man spricht nicht davon, dass die Menge bezüglich der Verknüpfung abgeschlossen ist, sondern dass die Verknüpfung auf der Menge abgeschlossen ist also nicht aus der Menge hinausführt.<br /> | ||
| + | --[[Benutzer:Jessy*|Jessy*]] 15:54, 15. Jan. 2013 (CET) Stimmt es nun so? | ||
| + | |||
=Beispiele für endliche Gruppen= | =Beispiele für endliche Gruppen= | ||
==Restklassen modulo 4== | ==Restklassen modulo 4== | ||
| − | <math>\mathbb{Z}_4:=\left\{ \overline{0}, \overline{1}, \overline{2}, \overline{3} \right\}</math> | + | <math>\mathbb{Z}_4:=\left\{ \overline{0}, \overline{1}, \overline{2}, \overline{3} \right\}</math><br /> |
| + | mit<br /> | ||
| + | <math>\overline{0}:=\left\{..., -8, -4, 0, 4, 8, ...\right\}</math> (Menge aller durch 4 teilbaren ganzen Zahlen),<br /> | ||
| + | <math>\overline{1}:=\left\{..., -7, -3, 1, 5, 9, ...\right\}</math> (Menge aller ganzen Zahlen, die bei Division durch 4 den Rest 1 lassen),<br /> | ||
| + | <math>\overline{2}:=\left\{..., -6, -2, 2, 6, 10, ...\right\}</math> (Menge aller ganzen Zahlen, die bei Division durch 4 den Rest 2 lassen),<br /> | ||
| + | <math>\overline{3}:=\left\{..., -5, -1, 3, 7, 11, ...\right\}</math> (Menge aller ganzen Zahlen, die bei Division durch 4 den Rest 3 lassen),<br /> | ||
| + | |||
| + | Wir definieren auf <math>\mathbb{Z}_4</math> eine Verknüpfung <math>\oplus</math> wie folgt:<br /> | ||
| + | <math>\forall \overline{a}, \overline{b} \in \mathbb{Z}_4: \overline{a}\oplus \overline{b} := \overline{a+b}</math> | ||
| + | |||
| + | Die Struktur <math>\left(\mathbb{Z}_4, \oplus\right)</math> ist eine Gruppe: | ||
| + | #Die Verknüpfung <math>\oplus</math> ist auf der Menge <math>\mathbb{Z}_4</math> abgeschlossen, d.h. <math>\forall \overline{a}, \overline{b} \in \mathbb{Z}_4: \overline{a} \oplus \overline{b} \in \mathbb{Z}_4</math>, | ||
| + | #Die Verknüpfung <math>\oplus</math> ist auf der Menge <math>\mathbb{Z}_4</math> assoziativ, d.h. <math>\forall \overline{a}, \overline{b}, \overline{c} \in \mathbb{Z}_4: \left(\overline{a} \oplus \overline{b} \right) \oplus \overline{c}= \overline{a} \oplus \left( \overline{b} \oplus \overline{c} \right)</math>, | ||
| + | #<math>\mathbb{Z}_4</math> hat ein neutrales Element, nämlich die Klasse <math>\overline{0}</math>, d.h. <math> \forall \overline{a} \in \mathbb{Z}_4: \overline{a} \oplus \overline{0}= \overline{0} \oplus \overline{a} = \overline{a}</math>,<br /> | ||
| + | #Zu jedem Element aus <math>\mathbb{Z}_4</math> gibt es ein inverses Element, d.h. <math>\forall \overline{a} \in \mathbb{Z}_4 \exist \left(-\overline{a}\right): \overline{a} \oplus \left(-\overline{a}\right) = \left(-\overline{a}\right) \oplus \overline{a} = \overline{0} </math>. | ||
| + | |||
| + | Die folgende Verknüpfungstafel verdeutlicht die obigen Eigenschaften: | ||
| + | |||
| + | <ggb_applet width="155" height="176" version="4.2" ggbBase64="UEsDBBQACAgIALGQiUEAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAgIALGQiUEAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s7Vptb9u2Fv7c/QpC2LfrxKJIyXbhdGic9G5AOxRNNwz3GyUxNhdZ1JUoOxn24+8hKcpyFDtVu9XA7YLGfDsvfA7PC+lm/sP9OkMbXlZC5hcePvc9xPNEpiJfXni1uj2bej+8+m6+5HLJ45KhW1mumbrw6Hng7fhgdE41r0gvvNvYj9KUpGeY3vIzGk34WRwn9CzhzJ9M6SyMb0MPoftKvMzlz2zNq4Il/CZZ8TV7KxOmjMiVUsXL8Xi73Z475eeyXI6Xy/j8vko9BBvPqwuv6bwEcXtMW2LIA9/H49/evbXiz0ReKZYn3EMaVC1effdivhV5KrdoK1K1AhNMAdiKi+UKUAZT2OlYExUAteCJEhteAWtnaDCrdeEZMpbr9Re2h7IWjodSsREpL7WRZ5OpH+D200OyFDxXDSluVI6dsPlG8K2VqntGoba+qESccTA4yypAJPLbEqzZjiv1kPGYle3EbjdkRGBd/AHEYCAPWROAat8f6d8g9EdUL4z3tcJWlZSZEQp0GP2JoAlsQxD603RCO6bNMLLDiWmwbxvcLE71x0wPoi9EhB0i8hSiyH8aEfVnkyOKVVnv6bXjnVq8U0u7aoMZGBFPRhNQG4Z9tfiLwLY6Zz4dALVzeD4KjdEDP/DRSDfYNgE0UWSXfDsHB2uawDbUNqGloZadWlJqaailoaSD0lpuyIk6kDgMPx0k/jI3wjulndOEaDD/zG9PJRkUiz0P+gyNEf0Sl/0MhRP/ayicj12imzeOiqqVpm18R/F1pV2XzIz3IoxCcNFoAs4WIjyDZqJTUYBwiGgIQzxFkW4niOjsQxFBU6TpMEHGR8MpfFCTmSIUgiw9ObEpChGKQoKw8WyKwJ+RiQ6IlIAARRiiEJi0dqzVkgjRCAZkiihsUMfFRCdIAnwwBuUBIhgRzYsnKIhQFKCJji1MdchFU713EBqgyEeRZoXggsCyQQUcU0Q0GvDwQlaiNe6KZ0V7KsaOIi9q1diumU/WqbOjko/IU5ncXT4yNmeVcn0ggmK0q3i2OO0VxBfzjMU8g1vDjfYDhDYs0yFs5N/KXCHnA4GdW5asWImkuuFKAVeFfmcb9pYpfv8GqCu3QaPa1Ok5r5NMpILlv4KTaBFaIHJl22RCV7anE2y1JFKW6c1DBZ6D7v/DSwmZGdPzWfcH0v+DXSKPl0BklTDt83S2vzKFQ3g4sDazuvmmxcbueeWMuSzNHcmaXw9+qi5ltpsqpMjVghWqLs0dDNJgqVG9zpcZN8Y1xR+uM8ldLO9vrFWJlfXxoYCRbzcQLxcykyWCkAx0Cl02bWxbQ6N31lL5hsY3FL47JpG263gWGArTxrY1VHDudmsNUuxgYt+pEZVJJCC862XGafTlqM6FeusGSiR3DVJs6X+u1zH4W8O2LxL/RSLn40ceNq+KkrO0WnGunvQ5U5icz+GoMQYw3S54lt10SXUCbS+VDWFHPJi4XufOQg1PMD1Gh1s64h+jCz6Rjuz0zo7R0R1d40MVz3QekDlCq5uklFlmUGw6/cTwa48Bb9Zn1UDL2IOsdW6AA3kDL4s6Y5eduqyn/92NFz3xo5X7mO7Xp6cvQV3Fy/dwlc72FiykHwEh3+f4ACrMLGqnWZbJ7Q1kO8Gy61Qo2VY5s/IRitVHUbQhzv9bA98HaETJ27TLaiUXcl1kXPFOetu3M/jNG/PCQs1L6x2DZB2MglE8wuFLOqK2E4yI7cBtyC2FbsYSj5LRGSFhSGYEyHFvzm9E7M/RJ+bC3hx9Ql7g9kbdbgO3Jep2S1wHPyGAOD7yxCLecQauE7oOdXyh69gZG9a9MJ7f8RLcwRaIHFJ0LevKVqzOsdQVf8/U6nWefuBL8O73TF93FOQMS7pLRSk4xhoY7XwT3Uzn618gB9nZlC9L7lJXZp6zNmOaVb9brnrTRtSbUq5/yjcfoRg82up87PDMq6QUha45KIb71x3fRU4qKga3t7TLB+ArQGFjVwmls6Px05V2cOBh2lNn6Ir/wXWyhCsQlG9dijO+hvcqUqbc5PWalyJpU+9lYJ7CsMna4Th3qQfiC8n4d8gXu8u35dqZE9YPlCQIt2LFtDzcL3H6ArBs2qbEOfq23EG+ARhd2xrt72Ta7BQ7i8OBGrPA1aGwChFcd7hNvKops6gAgaZKd/yG1fciE6x82HcTKC/Was/ab9GzH/677Pe59viK1rjqWSP4hq1x3bMG+Yat8Zr832War2k9+k+e6Vgj/CfPdKwRfVt5JpHrNctTlJtvtEC3t/sehfkX3vevCfoXuvweXlMM60eQRVkrR3BJrMhG0POXpMOp61Ns5//FyBaHkS0GIlv0kOFTIrs6jOxqILKrHrLglMiuDyO7HojsuoeMnAoZfSbO6MA4O1zkToHsWJwNRLboITuZN9Jn4mwgsqsespN647E4G4jsuofsZFk/fCbOwoFxdvj6dApkx+JsILJFD9nJvDF8Js4GIrvqITupNx6Ls4HIrnvITpb1o2fiLBoYZ4cv5qdAdizOBiJb9JCdzBujZ+JsILKrHrKTeuOxOBuI7LqH7G/K+uPud9Xm/4Sbvwl79T9QSwcIzlP2YogHAADCJgAAUEsBAhQAFAAICAgAsZCJQdY3vbkZAAAAFwAAABYAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhX2phdmFzY3JpcHQuanNQSwECFAAUAAgICACxkIlBzlP2YogHAADCJgAADAAAAAAAAAAAAAAAAABdAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAACAAIAfgAAAB8IAAAAAA==" showResetIcon = "false" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" /><br /><br /> | ||
| + | Die Tabelle wurde mit der Tabellenkalkulation von Geogebra generiert. Aus diesem Grunde fehlen die Querstriche über den Klassen. | ||
| + | |||
| + | Die Verknüpfungstabelle zeigt eine weitere Eigenschaft der Gruppe <math>\left(\mathbb{Z}_4, \oplus\right)</math>:<br /> | ||
| + | Die Ergebnisse in der Tabelle sind symmetrisch bezüglich der Hauptdiagonalen angeordnet. Letzteres bedeutet, dass die Verknüpfung <math>\oplus</math> auf <math>\mathbb{Z}_4</math> kommutativ ist:<br /> | ||
| + | *<math>\forall \overline{a}, \overline{b} \in \mathbb{Z}_4: \overline{a} \oplus \overline{b} = \overline{b} \oplus \overline{a}</math>.<br /> | ||
| + | Kommutative Gruppen werden auch Abelsche Gruppen genannt.<br /><br /> | ||
| + | ==Gruppe der Deckdrehungen des Quadrats== | ||
| + | Hierbei verstehen wir unter <math>D_Q</math> die Menge aller Drehungen die das Quadrat <math>\overline{ABCD}</math> auf sich selbst abbilden:<br /> | ||
| + | <math>D_Q:=\left\{D_{0}, D_{90}, D_{180}, D_{270}\right\}</math><br /><br /> | ||
| + | Die Verknüpfung sei die NAF.<br /><br /> | ||
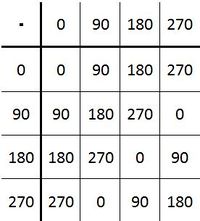
| + | Daraus ergibt sich folgende Verknüpfungstafel:<br /> | ||
| + | [[Bild:Verknüpfungstafel_DR.3JPG.JPG| 200px]]<br /><br /> | ||
| + | <u>'''Überprüfung der Gruppeneigenschaften:'''</u><br /> | ||
| + | 1. Abgeschlossenheit: siehe Verknüpfungstabelle<br /> | ||
| + | 2. Assoziativität: Drehungen sind immer assoziativ<br /> | ||
| + | 3. Neutrales Element: <math>D_{0}</math><br /> | ||
| + | 4. Inverse Elemente: <math>D_{0} \cdot D_{0}= D_{0}</math> und <math>D_{90} \cdot D_{270} = D_{0}</math> und <math>D_{180} \cdot D_{180} = D_{0}</math> und <math>D_{270} \cdot D_{90} = D_{0}</math><br /> | ||
| + | 5. Kommutativ: Drehungen sind immer kommutativ<br /><br /> | ||
| + | Es handelt sich also sogar um eine abelsche Gruppe.<br /><br /> | ||
| + | Anmerkung: Die Gruppe der Deckdrehungen des Quadrats ist eine zyklische Gruppe.<br /><br /> | ||
| + | --[[Benutzer:Jessy*|Jessy*]] 16:26, 11. Dez. 2012 (CET)<br /><br /> | ||
| + | |||
| + | ==Gruppe der Deckabbildungen des Rechtecks== | ||
| + | [[Bild:Decvkabbildungen_Rechteck.png| 300px]]<br /> | ||
| + | Unter <math>D_R</math> wollen wir die Menge aller Bewegungen verstehen, die das Rechteck <math>\overline{ABCD}</math> auf sich selbst abbilden. Es handelt sich dabei um die folgenden Drehungen (mit dem Drehzentrum <math>Z</math>) und Geradenspiegelungen:<br /> | ||
| + | <math>D_R:=\left\{D_{0}, D_{180}, S_m, S_n\right\}</math><br /><br /> | ||
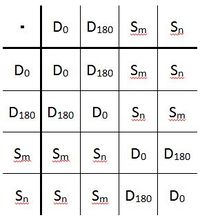
| + | Es ergibt sich folgende Verknüpfungstafel:<br /> | ||
| + | [[Bild:Verknüpfungstafel_DR.4.JPG| 200px]]<br /><br /> | ||
| + | <u>'''Überprüfung der Gruppeneigenschaften:'''</u><br /> | ||
| + | 1. Abgeschlossenheit: siehe Verknüpfungstabelle<br /> | ||
| + | 2. Assoziativität: Gegeben <br /> | ||
| + | 3. Neutrales Element: <math>D_{0}</math><br /> | ||
| + | 4. Inverse Elemente: <math>D_{0} \cdot D_{0}= D_{0}</math> und <math>D_{180} \cdot D_{180} = D_{0}</math> und <math>S_{m} \cdot S_{m} = D_{0}</math> und <math>S_{n} \cdot S_{n} = D_{0}</math><br /><br /> | ||
| + | Anmerkung: Die Gruppe der Deckabbildungen des Rechtecks ist die kleinste nicht-zyklische Gruppe und wird auch '''Kleinsche Vierergruppe''' genannt.<br /><br /> | ||
| + | --[[Benutzer:Jessy*|Jessy*]] 10:17, 12. Dez. 2012 (CET)<br /><br /> | ||
| + | |||
| + | |||
| + | |||
| + | <!--- hier drunter nichts eintragen ---> | ||
| + | [[Kategorie:Linalg]] | ||
| + | |||
| + | |} | ||
| + | </div> | ||
Aktuelle Version vom 15. Januar 2013, 15:54 Uhr
|
GruppeneigenschaftenEine Verknüpfung Bemerkung --*m.g.* 14:14, 12. Dez. 2012 (CET): Beispiele für endliche GruppenRestklassen modulo 4
Wir definieren auf Die Struktur
Die folgende Verknüpfungstafel verdeutlicht die obigen Eigenschaften:
Die Tabelle wurde mit der Tabellenkalkulation von Geogebra generiert. Aus diesem Grunde fehlen die Querstriche über den Klassen. Die Verknüpfungstabelle zeigt eine weitere Eigenschaft der Gruppe
Kommutative Gruppen werden auch Abelsche Gruppen genannt. Gruppe der Deckdrehungen des QuadratsHierbei verstehen wir unter Gruppe der Deckabbildungen des Rechtecks
|
 bzw. einer Operation auf einer Menge M ist eine Gruppe, wenn folgende Eigenschaften erfüllt sind:
bzw. einer Operation auf einer Menge M ist eine Gruppe, wenn folgende Eigenschaften erfüllt sind: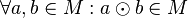
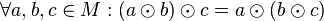
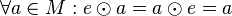
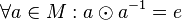 mit
mit 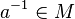 und e = neutrales Element
und e = neutrales Element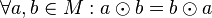
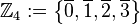
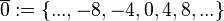 (Menge aller durch 4 teilbaren ganzen Zahlen),
(Menge aller durch 4 teilbaren ganzen Zahlen),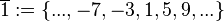 (Menge aller ganzen Zahlen, die bei Division durch 4 den Rest 1 lassen),
(Menge aller ganzen Zahlen, die bei Division durch 4 den Rest 1 lassen),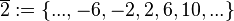 (Menge aller ganzen Zahlen, die bei Division durch 4 den Rest 2 lassen),
(Menge aller ganzen Zahlen, die bei Division durch 4 den Rest 2 lassen),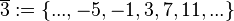 (Menge aller ganzen Zahlen, die bei Division durch 4 den Rest 3 lassen),
(Menge aller ganzen Zahlen, die bei Division durch 4 den Rest 3 lassen), eine Verknüpfung
eine Verknüpfung  wie folgt:
wie folgt: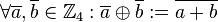
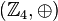 ist eine Gruppe:
ist eine Gruppe:
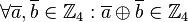 ,
,
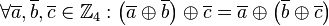 ,
,
 , d.h.
, d.h. 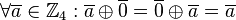 ,
,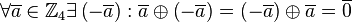 .
.
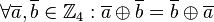 .
.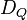 die Menge aller Drehungen die das Quadrat
die Menge aller Drehungen die das Quadrat  auf sich selbst abbilden:
auf sich selbst abbilden: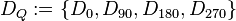
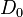
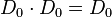 und
und 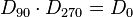 und
und 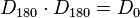 und
und 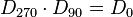
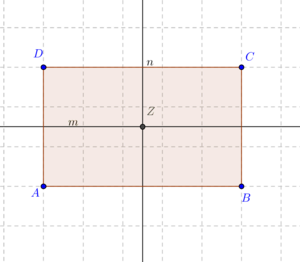
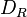 wollen wir die Menge aller Bewegungen verstehen, die das Rechteck
wollen wir die Menge aller Bewegungen verstehen, die das Rechteck  ) und Geradenspiegelungen:
) und Geradenspiegelungen: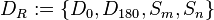
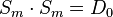 und
und