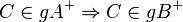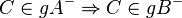Lösung von Aufgabe 8.6 (WS 12 13): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
Yellow (Diskussion | Beiträge) (→Lösung von User ...) |
|||
| (8 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 17: | Zeile 17: | ||
==Lösung von User ...== | ==Lösung von User ...== | ||
| − | [[Bild:8.6a.jpg | | + | <br />[[Bild:8.6a.jpg | 500px]] |
--[[Benutzer:Yellow|Yellow]] 17:01, 18. Dez. 2012 (CET) | --[[Benutzer:Yellow|Yellow]] 17:01, 18. Dez. 2012 (CET) | ||
| + | @ yellow Hallöle du hast als zweite Voraussetzung dass a,b,c element von g ist. dass verstehe ich nicht ganz??? | ||
==Lösung von User ...== | ==Lösung von User ...== | ||
| − | + | [[Bild:8.6b.jpg | 500px]] | |
| + | --[[Benutzer:Yellow|Yellow]] 17:26, 18. Dez. 2012 (CET) | ||
| + | |||
| + | {{#ev:youtube|LCTHgm1wlBU}} | ||
<!--- Was hier drunter steht muss stehen bleiben ---> | <!--- Was hier drunter steht muss stehen bleiben ---> | ||
|} | |} | ||
Aktuelle Version vom 11. Januar 2013, 14:21 Uhr
Aufgabe 8.6Es sei Beweisen Sie:
Lösung von User ...
--Yellow 17:01, 18. Dez. 2012 (CET) @ yellow Hallöle du hast als zweite Voraussetzung dass a,b,c element von g ist. dass verstehe ich nicht ganz??? Lösung von User ...
|
eine Gerade der Ebene 
. Ferner seien 
drei nicht kollineare Punkte der Ebene Epsilon. Keiner dieser drei Punkte möge zu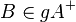 
.
