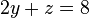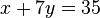Lösungen zu den Aufgaben 2: Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(Die Seite wurde neu angelegt: „==2.1== ==2.2== Man betrachte den Steigungswinkel <math>\alpha</math> am Steigungsdreieck. Mit der Steigung und dem <math>tan\alpha</math> berechnen Sie den Win…“)
 
(→‎2.1)
 
(2 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt)
Zeile 1: Zeile 1:
 
==2.1==
 
==2.1==
−
 
+
Berechnen Sie die Werte. Zur Kontrolle beachten (und verändern) Sie die GeoGebra Applikation im Wiki des Algorithmus von Bresenham.
  
 
==2.2==
 
==2.2==
Zeile 14: Zeile 14:
 
<math>m=\frac{y_2-y_1}{x_2-x_1}=\frac{-\frac{1}{2}}{-4}=\frac{1}{8}</math><br />
 
<math>m=\frac{y_2-y_1}{x_2-x_1}=\frac{-\frac{1}{2}}{-4}=\frac{1}{8}</math><br />
 
<math>\tan\alpha=\frac{1}{8} \Rightarrow \alpha = 7,125^\circ </math>
 
<math>\tan\alpha=\frac{1}{8} \Rightarrow \alpha = 7,125^\circ </math>
 +
 +
==2.3==
 +
 +
Der Beweis erfolgt durch Einsetzen der Punkte in die Gleichung und Umstellen ;-).
 +
 +
==2.4==
 +
<math>ax+by+cz=d</math> bezeichnet eine Ebene im <math>\mathbb{R}^3</math>.<br />
 +
Es seien zwei Ebenen gegeben.<br />
 +
<math>e_1: a_1 x+b_1 y+c_1 z=d_1 </math><br />
 +
<math>e_2: a_2 x+b_2 y+c_2 z=d_2</math><br />
 +
Die Lösungsmenge, die auf beide Ebenen passt entspricht der Schnittgerade. Damit kann also eine Gerade im <math>\mathbb{R}^3</math> mit zwei Gleichungen dargestellt werden. Allerdings sind diese Gleichungen nicht eindeutig.<br />
 +
Zur Bestimmung des Linearen Gleichungssystems, dass die Gerade durch die Punkte P, Q bestimmt, werden die beide Punkte je in die Gleichung  <math>e_1</math> und <math>e_2</math> eingesetzt.<br />
 +
 +
<math> 5b_1 -2c_1=d_1 </math><br />
 +
<math>14a_1+3b_1 y+2c_1=d_1</math><br />
 +
 +
 +
<math> 5b_2 -2c_2=d_2 </math><br />
 +
<math>14a_2+3b_2 y+2c_2=d_2</math><br />
 +
 +
'''Lösung der LGS'''<br />
 +
 +
Gauß ergibt:<br />
 +
<math>7a_1+4b_1=d_1</math> und <math>7a_2+4b_2=d_2</math><br />
 +
Jeweils zwei Werte können frei gewählt werden, allerdings ist dabei zu achten, dass keine Vielfachen der Gleichungen entstehen. Damit lassen sich die Punkte durch folgedens LGS beschreiben:<br />
 +
<math>2y+z=8</math><br />
 +
<math>x+7y=35</math>

Aktuelle Version vom 27. Dezember 2012, 15:17 Uhr

Inhaltsverzeichnis

2.1

Berechnen Sie die Werte. Zur Kontrolle beachten (und verändern) Sie die GeoGebra Applikation im Wiki des Algorithmus von Bresenham.

2.2

Man betrachte den Steigungswinkel \alpha am Steigungsdreieck. Mit der Steigung und dem 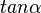tan\alpha berechnen Sie den Winkel.
a) 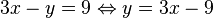3x-y=9 \Leftrightarrow y=3x-9 .
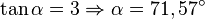
\tan\alpha=3 \Rightarrow \alpha = 71,57^\circ

b) 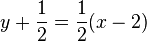y + \frac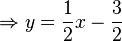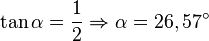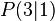{1}{2}=\frac{1}{2}(x-2)
\Rightarrow y=\frac{1}{2}x-\frac{3}{2}
\tan\alpha=\frac{1}{2} \Rightarrow \alpha = 26,57^\circ

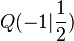
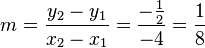
c) P(3|1) und Q(-1|\frac{1}{2}) m=\frac{y_2-y_1}{x_2-x_1}=\frac{-\frac{1}{2}}{-4}=\frac{1}{8}
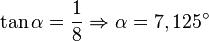
\tan\alpha=\frac{1}{8} \Rightarrow \alpha = 7,125^\circ

2.3

Der Beweis erfolgt durch Einsetzen der Punkte in die Gleichung und Umstellen ;-).

2.4

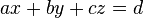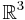ax+by+cz=d bezeichnet eine Ebene im \mathbb{R}^3.
Es seien zwei Ebenen gegeben.
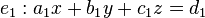
e_1: a_1 x+b_1 y+c_1 z=d_1
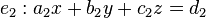
e_2: a_2 x+b_2 y+c_2 z=d_2
Die Lösungsmenge, die auf beide Ebenen passt entspricht der Schnittgerade. Damit kann also eine Gerade im 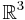\mathbb{R}^3 mit zwei Gleichungen dargestellt werden. Allerdings sind diese Gleichungen nicht eindeutig.
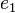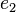Zur Bestimmung des Linearen Gleichungssystems, dass die Gerade durch die Punkte P, Q bestimmt, werden die beide Punkte je in die Gleichung e_1 und e_2 eingesetzt.

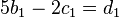
5b_1 -2c_1=d_1
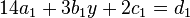
14a_1+3b_1 y+2c_1=d_1


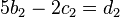
5b_2 -2c_2=d_2
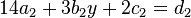
14a_2+3b_2 y+2c_2=d_2

Lösung der LGS

Gauß ergibt:
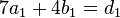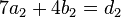
7a_1+4b_1=d_1 und 7a_2+4b_2=d_2
Jeweils zwei Werte können frei gewählt werden, allerdings ist dabei zu achten, dass keine Vielfachen der Gleichungen entstehen. Damit lassen sich die Punkte durch folgedens LGS beschreiben:
2y+z=8
x+7y=35

Von „http://geometrie.zum.de/index.php?title=Lösungen_zu_den_Aufgaben_2&oldid=19912“