Lösung von Aufgabe 9.4P (WS 12 13): Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: „''m'' sei Mittelsenkrechte der Strecke <math>\overline{AB}</math>. Beweisen Sie durch Kontraposition: <math>\left| AP \right| =\left| BP \right|\Rightarrow P\in …“) |
|||
| (Eine dazwischenliegende Version von einem Benutzer wird nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
''m'' sei Mittelsenkrechte der Strecke <math>\overline{AB}</math>. Beweisen Sie durch Kontraposition: <math>\left| AP \right| =\left| BP \right|\Rightarrow P\in m</math> | ''m'' sei Mittelsenkrechte der Strecke <math>\overline{AB}</math>. Beweisen Sie durch Kontraposition: <math>\left| AP \right| =\left| BP \right|\Rightarrow P\in m</math> | ||
<br />Tipp: Nutzen Sie den Satz von Pasch und die Dreiecksungleichung. <br />Hinweis: Die Umkehrung des hier zu beweisenden Satzes sei bereits bewiesen.<br /> | <br />Tipp: Nutzen Sie den Satz von Pasch und die Dreiecksungleichung. <br />Hinweis: Die Umkehrung des hier zu beweisenden Satzes sei bereits bewiesen.<br /> | ||
| + | |||
| + | In der Vorlesung hat Herr Schnirch schon den Tipp gegeben, den Beweis indirekt zu führen. Ob man nun die Kontraposition oder einen Widerspruchsbeweis wählt, ist egal. (Es handelt sich um die selben Schritte. | ||
| + | Ich mache hier mal den Anfang. | ||
| + | |||
| + | |||
| + | {| class="wikitable" | ||
| + | | Voraussetzung || ''m'' sei Mittelsenkrechte der Strecke <math>\overline{AB}</math>. <math>\left| AP \right| =\left| BP \right|</math> | ||
| + | |- | ||
| + | | Behauptung || <math>P\in m</math> | ||
| + | |- | ||
| + | | Annahme || <math>P \not\in m </math> | ||
| + | |} | ||
| + | <br /> | ||
| + | Fallunterscheidung je nach Lage von P.<br /> Nach der Annahme liegt P entweder auf AB (Fall 1), oder in der Halbebenen gA^+ (ohne auf AB zu liegen)(Fall 2) oder in gA- (Fall 3). <br /> | ||
| + | Fall 1 kann nicht eintreten, da P nach Voraussetzung ja Mittelpunkt der STrecke AB wäre und damit auf m liegen würde.<br /> | ||
| + | Fall 2 genauer zu betrachen und zum Widerspruch zu führen.<br /> | ||
| + | Fall 3 lässt sich analog zu Fall 2 beweisen. (Nicht extra nötig)--[[Benutzer:Tutorin Anne|Tutorin Anne]] 13:04, 14. Jan. 2013 (CET)<br /><br /> | ||
| + | |||
| + | <ggb_applet width="585" height="422" version="4.2" ggbBase64="UEsDBBQACAAIAC1pLkIAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAAIAC1pLkIAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s1Vjbbtw2EH1OvmKg53iX1H2D3QRxgKApnNSo06LoS0BJ9C5jraSK3FuQz+mf9Mc6Q0p7s53UjlMktncpksMZzpnDGcrj5+t5CUvZalVXE48PmAeyyutCVdOJtzCXJ6n3/Nnj8VTWU5m1Ai7rdi7MxAsHvrdbh70Bj2ixKiZekMXJKBsVJyIK2UmY5Pwki7E7KpKChVmeiMtLD2Ct1dOqfivmUjcilxf5TM7FWZ0LY3XOjGmeDoer1WrQWx/U7XQ4nWaDtS48wJ1XeuJ1D09R3cGiVWDFfcb48I83Z079iaq0EVUuPSCvFurZ40fjlaqKegUrVZjZxIs5ejaTajojN9PUgyEJNehrI3OjllLj0r2u9dnMG8+KiYrmH7knKLfueFCopSpkO/HYwE+TKOXxaBSEccgiNFi3Slamk+WdzWGvbbxUcuXU0pO1GLJRgiFQWmWlnHiXotTolaouW0QUN9QusKvNppSZaPv+bj/8Cf6igPooSReGzsGAM4w9oU+Cnyhibi/7hj0wdV1arQyiEXz6BD7zGTyhhrvGxyaO3RRzYyxwje+a0DWRkwnd8tCJhk4mdDJh8Bk/u/7O0W7gwNPez+AmP2P8WACO/OR7Vh16txu9hm5vMUqj/27R/yo/g96mf5OXfnSzzXQvmpxC9Qk4xcg2AVB0uI0SNWHXjV03sQ1nruHdZEpflhXxw/jDk/gOUfs6o9vA8WgPRMTO/tnPNZPBneJ2K1XuYDEOv+bk38Ngwv4Pg+Nhn+fGHSdBz0i2O35GzjXlnGBk0w5wiJCwcYJZIgI+wiYh4vrAIwgj7PIUYmoTCIirIQSQAsnxAGxyiVL8Ci2PY4hQFw0mjtAQhBAFwG1KCgETEdi0hinOD1AiiiDCRWSdk9kghjDGTpBCiBukhJbQcQpwHfbRuA8Bh4DW8gT8GGIfEkqKPKRcGae0d1TqQ8wgpqWYFTEjumyIK1IIyBtkeFNrtQV3JstmGxWLo6qahTnALp8X/aOpj6SLOr86PcJaCm36ZxTCUrQreK40HdTDR+NSZLLEW8MF0QBgKUo6wVb/ZV0Z6Cngu7FpK5qZyvWFNAZXafggluJMGLl+hdK636A1bcv0WC7yUhVKVL8jR0gFKYS+ats821ftwO8s53XdFhcbjcSB9Z+yrTE5unvKxvUC6u3/ILY6F8TycDQY7f9gsd3cMpU6a3K59Uas5dYHmLZ0hPY6r/VpXe6GmlpV5qVozKK11y5MfC058qKaltLiaUsDXmDyq6xeXzggA6fr3abBHnM7yKYv67JuAQ+hHyEg067NXGtlaGtbKWZlmJVgfWRUsZ3nI99K2DZzrZXCULutda7y3k3OejNK29SByh2x+lxLRKH70KJS5qzvGJVfda5yt+DtYp4hxzoSHurkD6VzPDyi1fhKtpUsHXkqDOaiXmjH5i0jH40XWp4LM3tRFb/KKR7Dc0GZ0KBqJ7rbciFzNceFbrwDT1Bgf8OtutFCTlvZu1jam66D1s6yfSpfG7aqXrX1/HW1fIesOdrqeNj7M9Z5qxpiJ2SYmq/kjn+F0gITe7G/Dp3X6EVOSQaBNASiB2JhZnVrL7N4VBHWEH7+5++qki1mR2QkHdNSzvEmC8by0lJ7G58X9opMgYA6+4DJY1sr3PwONpy+kaOWzaJsZoKu0R0GpdjgBvZRsfre1MUxVhgK6xAmhMaRopHS8cntFx8aVGeP4V68Lfga1hPvxB8EWHw39K6U4N3po3tpcq8I5CydzoPs50aPAoe8czh9AbHTHx8xfxBbvLANHwSvvJ7PRVVAZS8fF3JK496u7AlGTAPBCT6HzcL0E8Jp63RcQ1932np8xRfw3/P4tgCw+8O/Rzs2SOODQsUtqOFgFByUoshCfMJRnkXxca42WHKv8JVS24JiutJhH35SRSHtfaKHrKSgvq4oq0mbB67nwSspGypAv1TvWlFp+ufAYQK8PW5nuKlTRZrr9ih44lrUss9HjRzchiT7XkJ2U2w2t4TyI52PKPTTg6vIvaMn/6rcEu3Kn5o3pcqVuUvqOX/v//jJB9M1T7uTEvrfIP2cW8y+xN/z9/zzDD6Gnt8Leu67O59tvwv4+cAP0igOkNkxJqQuFnwwSngSpixOWMJTusp+4zp6/j748cnsD/yey+xhuDzcv+bZV63uP63P/gVQSwcI4SjSHlwGAAAZFgAAUEsBAhQAFAAIAAgALWkuQtY3vbkZAAAAFwAAABYAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhX2phdmFzY3JpcHQuanNQSwECFAAUAAgACAAtaS5C4SjSHlwGAAAZFgAADAAAAAAAAAAAAAAAAABdAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAACAAIAfgAAAPMGAAAAAA==" showResetIcon = "false" enableRightClick = "true" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "true" showToolBar = "true" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" /> | ||
| + | <br /> | ||
| + | Fall 2: <br /> | ||
| + | {| class="wikitable" | ||
| + | !Beweisschritt!!Begründung | ||
| + | |- | ||
| + | | 1 (Schritt 1 hier)|| (Begründung 1) | ||
| + | |- | ||
| + | | 2 (Schritt 2) || (Begründung 2) | ||
| + | |- | ||
| + | | 3 (Schritt) || (Begründung) | ||
| + | |- | ||
| + | | 4 (Schritt) || (Begründung und weitere Schritte ergänzen) | ||
| + | |} | ||
| + | <br /> | ||
| + | |||
[[Kategorie:Einführung_P]] | [[Kategorie:Einführung_P]] | ||
Aktuelle Version vom 14. Januar 2013, 13:10 Uhr
m sei Mittelsenkrechte der Strecke  . Beweisen Sie durch Kontraposition:
. Beweisen Sie durch Kontraposition: 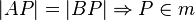
Tipp: Nutzen Sie den Satz von Pasch und die Dreiecksungleichung.
Hinweis: Die Umkehrung des hier zu beweisenden Satzes sei bereits bewiesen.
In der Vorlesung hat Herr Schnirch schon den Tipp gegeben, den Beweis indirekt zu führen. Ob man nun die Kontraposition oder einen Widerspruchsbeweis wählt, ist egal. (Es handelt sich um die selben Schritte. Ich mache hier mal den Anfang.
| Voraussetzung | m sei Mittelsenkrechte der Strecke  . . 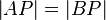
|
| Behauptung | 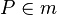
|
| Annahme | 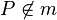
|
Fallunterscheidung je nach Lage von P.
Nach der Annahme liegt P entweder auf AB (Fall 1), oder in der Halbebenen gA^+ (ohne auf AB zu liegen)(Fall 2) oder in gA- (Fall 3).
Fall 1 kann nicht eintreten, da P nach Voraussetzung ja Mittelpunkt der STrecke AB wäre und damit auf m liegen würde.
Fall 2 genauer zu betrachen und zum Widerspruch zu führen.
Fall 3 lässt sich analog zu Fall 2 beweisen. (Nicht extra nötig)--Tutorin Anne 13:04, 14. Jan. 2013 (CET)
Fall 2:
| Beweisschritt | Begründung |
|---|---|
| 1 (Schritt 1 hier) | (Begründung 1) |
| 2 (Schritt 2) | (Begründung 2) |
| 3 (Schritt) | (Begründung) |
| 4 (Schritt) | (Begründung und weitere Schritte ergänzen) |

