Lösung von Aufgabe 10.2P (WS 12 13): Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
 
Zeile 76: Zeile 76:
  
 
--[[Benutzer:Kaeseknilch|Kaeseknilch]] 17:38, 20. Jan. 2013 (CET)<br />
 
--[[Benutzer:Kaeseknilch|Kaeseknilch]] 17:38, 20. Jan. 2013 (CET)<br />
−
*Danke Kaeseknilch, ich habe mich wohl nicht deutlich ausgedrückt. Dein Beweis ist fast richtig. Der letzte Schritt kannst du nicht so scheiben. Es würde bedeuten, dass die beiden Winkel identisch sind - und das sind sie nicht.
+
*Danke Kaeseknilch, ich habe mich wohl nicht deutlich ausgedrückt. Dein Beweis ist fast richtig. Den letzten Schritt kannst du nicht so scheiben. Es würde bedeuten, dass die beiden Winkel identisch sind - und das sind sie nicht.
 
*Der Beweis kann natürlich auch ausführlicher geführt werden. Schritt 4) und 5) kann ebenso mit Def. Geradenspiegelung begründet werden.--[[Benutzer:Tutorin Anne|Tutorin Anne]] 09:20, 25. Jan. 2013 (CET)<br /><br />
 
*Der Beweis kann natürlich auch ausführlicher geführt werden. Schritt 4) und 5) kann ebenso mit Def. Geradenspiegelung begründet werden.--[[Benutzer:Tutorin Anne|Tutorin Anne]] 09:20, 25. Jan. 2013 (CET)<br /><br />
  
−
Es müsste heißen: 6) Winkel MAC <math> \tilde {=}</math>  Winkel MBC oder: <math>\left| \angle MAC  \right| = \left| \angle MBC  \right|</math><br /> Meintest du das Anne?--[[Benutzer:TobiWan|TobiWan]] 10:49, 26. Jan. 2013 (CET)
+
Es müsste heißen: 6) Winkel MAC <math> \tilde {=}</math>  Winkel MBC oder: <math>\left| \angle MAC  \right| = \left| \angle MBC  \right|</math><br /> Meintest du das Anne?--[[Benutzer:TobiWan|TobiWan]] 10:49, 26. Jan. 2013 (CET)<br /><br />
 +
* Ja! So stimmt's dann!--[[Benutzer:Tutorin Anne|Tutorin Anne]] 13:33, 28. Jan. 2013 (CET)

Aktuelle Version vom 28. Januar 2013, 13:33 Uhr

Beweisen Sie mit abbildungsgeometrischen Mitteln den Basiswinkelsatz.

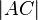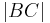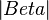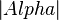
Voraussetzung: gleichschenkliges Dreieck mit \left| AC \right| = \left| BC \right| Behauptung: \left| Beta \right| = \left| Alpha \right|

Schritt Beobachtung
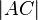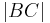
1) \left| AC \right| = \left| BC \right| Vor.
2) m ist Mittelsenkrechte von AB; C \in m 1; Mittelsenkrechtenkriterium
3) Sm (A) = B 2; Def. Geradenspiegelung
4) Sm (C) = C Def. Fixpunkt
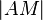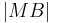
5) \left| AM \right| = \left| MB \right| Def. Mittelsenkrechte
6) Winkel CAM = \alpha; Winkel CBM =\beta Def. Winkel
7) Sm (\alpha) = \beta 5; winkelmaßerhaltung

--Hakunamatata 21:47, 16. Jan. 2013 (CET)

Zwei Anmerkungen dazu:

  • Warum folgt aus Schritt 1) C \in m?
  • Da du bestimmte Schritte zur Begründung weiterer Schritte nicht verwendet hast, brauchst du sie auch nicht. Oder doch? Für welche Schritte? Bitte ergänzt die Nummern, oder die Schritte können weg gelassen werden.--Tutorin Anne 16:03, 17. Jan. 2013 (CET)

Bei meinem ersten Schritt fehlt etwas ;-) So jetzt ist es ergänzt. Wissen wir nicht, dass der Punkt c Element m ist, dadurch das wir ein gleichschenkliges Dreieck haben?!? --Hakunamatata 17:39, 17. Jan. 2013 (CET)

Also passt es jetzt so?? --Hakunamatata 18:09, 19. Jan. 2013 (CET)
Nein, entweder du nutz alle Schritte von 1-6 für irgendwelche Begründungen oder du streichst all die jenigen raus, die du nicht zum Begründen genutzt hast.--Tutorin Anne 12:36, 20. Jan. 2013 (CET)

Damit ihr 2 hier nicht alleine diskutieren müsst..Hier mal meine Tabelle, abgeleitet von oben. Was Anne einfach meint ist (glaube ich), dass du die Schritte bei den Begründungen angeben musst, weil sonst der Schritt keine Berechtigung für den weiteren Beweisverlauf hat. Außerdem ist die Bezeichnung der Winkel (Schritt 6) überflüssig (siehe Wiki-Seite "Der Basiswinkelsatz").--Kaeseknilch 17:38, 20. Jan. 2013 (CET)

Schritt Begründung
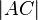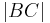
1) \left| AC \right| = \left| BC \right| Vor.
2) m ist Mittelsenkrechte von AB; C \in m 1), Mittelsenkrechtenkriterium
3) Sm (A) = B 2), Def. Geradenspiegelung
4) Sm (C) = C 2), Def. Fixpunkt
5) M = Sm(M) 2), Def. Fixpunkt
6) Winkel MAC = Winkel MBC 3),4),5), Def. Winkeltreue

--Kaeseknilch 17:38, 20. Jan. 2013 (CET)

  • Danke Kaeseknilch, ich habe mich wohl nicht deutlich ausgedrückt. Dein Beweis ist fast richtig. Den letzten Schritt kannst du nicht so scheiben. Es würde bedeuten, dass die beiden Winkel identisch sind - und das sind sie nicht.
  • Der Beweis kann natürlich auch ausführlicher geführt werden. Schritt 4) und 5) kann ebenso mit Def. Geradenspiegelung begründet werden.--Tutorin Anne 09:20, 25. Jan. 2013 (CET)

Es müsste heißen: 6) Winkel MAC 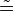\tilde {=} Winkel MBC oder: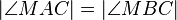 \left| \angle MAC \right| = \left| \angle MBC \right|
Meintest du das Anne?--TobiWan 10:49, 26. Jan. 2013 (CET)

  • Ja! So stimmt's dann!--Tutorin Anne 13:33, 28. Jan. 2013 (CET)
Von „http://geometrie.zum.de/index.php?title=Lösung_von_Aufgabe_10.2P_(WS_12_13)&oldid=20997“