Lösung Aufgabe 11.03 WS 12 13: Unterschied zwischen den Versionen
Hauler (Diskussion | Beiträge) |
*m.g.* (Diskussion | Beiträge) (→Frage) |
||
| Zeile 36: | Zeile 36: | ||
--[[Benutzer:Hauler|Hauleri]] 13:05, 26. Jan. 2013 (CET) | --[[Benutzer:Hauler|Hauleri]] 13:05, 26. Jan. 2013 (CET) | ||
| + | =Antwort--[[Benutzer:*m.g.*|*m.g.*]] 14:33, 26. Jan. 2013 (CET)= | ||
| + | Was sollte nicht stimmen? Wir haben die Aufgabe im Prinzip in der Übung vom 18.02.13 gelöst. Nur haben wir es dort indirekt gemacht. | ||
| + | Also noch mal: | ||
| + | *Wir gehen davon aus, dass wir einen Winkel mit seiner Winkelhalbierenden haben. | ||
| + | *Auf der Winkelhalbierenden wählen wir einen beliebigen Punkt. | ||
| + | *Von diesem Punkt aus fällen wir das Lot auf einen Schenkel des Winkels. | ||
| + | *Wir messen den Abstand des Fußpunktes dieses Lotes zum Scheitel des Winkels. | ||
| + | *Den so gewonnenen Abstand tragen wir auf dem anderen Schenkel des Winkels ab. | ||
| + | *Wir behaupten jetzt, dass der so gewonnene Punkt der Fußpunkt des Lotes von dem Punkt auf der Winkelhalbierenden auf den anderen Schenkel des Winkels ist. | ||
| + | Wo ist Ihr Problem mit der Aufgabenstellung? | ||
<!--- Was hier drunter steht muss stehen bleiben ---> | <!--- Was hier drunter steht muss stehen bleiben ---> | ||
|} | |} | ||
Aktuelle Version vom 26. Januar 2013, 14:33 Uhr
Aufgabe 11.03Es sei
Berichtigung der Erstfassung(Muss es nicht korrekterweise heißen: Beweisen Sie: War natürlich ein Fehler, hab's geändert, danke. --*m.g.* 19:34, 21. Jan. 2013 (CET)) Anfrage Sallie FieldDürfen wir bei diesem Beweis die euklidische Geometrie anwenden und einfach über die Innenwinkelsumme im Dreieck gehen? Lösung User ...
Kommentar --*m.g.* 10:01, 25. Jan. 2013 (CET)
FrageIrgendwie stimmt doch etwas in der Aufgabenstellung nicht oder?? --Hauleri 13:05, 26. Jan. 2013 (CET) Antwort--*m.g.* 14:33, 26. Jan. 2013 (CET)Was sollte nicht stimmen? Wir haben die Aufgabe im Prinzip in der Übung vom 18.02.13 gelöst. Nur haben wir es dort indirekt gemacht. Also noch mal:
Wo ist Ihr Problem mit der Aufgabenstellung? |
 ein Winkel mit den Schenkeln
ein Winkel mit den Schenkeln  und
und  und dem Scheitel
und dem Scheitel  . Ferner sei
. Ferner sei  die Winkelhalbierende von
die Winkelhalbierende von 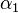 und
und 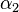 teilt. Auf
teilt. Auf  gegeben.
gegeben. 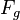 sei der Fußpunkt des Lotes von
sei der Fußpunkt des Lotes von 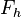 , indem wir auf
, indem wir auf 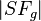 abtragen:
abtragen:

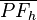 das Lot von
das Lot von 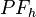 senkrecht auf
senkrecht auf 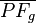 das Lot von
das Lot von 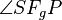 ein Rechter sein ... .
ein Rechter sein ... .

