Lösung von Zusatzaufgabe 8.1P (WS 12 13): Unterschied zwischen den Versionen
| Zeile 3: | Zeile 3: | ||
[[Datei:lwl.jpg|500px]] | [[Datei:lwl.jpg|500px]] | ||
<br /> | <br /> | ||
| − | Ich steche in P ein, stelle den Zirkel bis zum Scheitel des Winkels Bete ein, mache einen Bogen um P, sodass ein Schnittpunkt S1 mit der Halbgeraden DC+ entsteht, dann verbinde ich P mit S1. Jetzt steche ich in S1 ein und zeichen einen Bogen um S1 mit dem Radius |SP|, bis ein Schnittpunt S2 mit der Halbgeraden AB+ entsteht. Ich verbinde S1 und S2. Liegt S2 außerhalb der Strecke AB schneidet die Strecke S1S2 BC und die Aufgabe ist gelöst. Wenn nicht, muss der Vorgang erneut wiederholt werden.--[[Benutzer:Unicycle|Unicycle]] 17:48, 26. Jan. 2013 (CET) | + | Ich steche in P ein, stelle den Zirkel bis zum Scheitel des Winkels Bete ein, mache einen Bogen um P, sodass ein Schnittpunkt S1 mit der Halbgeraden DC+ entsteht, dann verbinde ich P mit S1. Jetzt steche ich in S1 ein und zeichen einen Bogen um S1 mit dem Radius |SP|, bis ein Schnittpunt S2 mit der Halbgeraden AB+ entsteht. Ich verbinde S1 und S2. Liegt S2 außerhalb der Strecke AB schneidet die Strecke S1S2 BC und die Aufgabe ist gelöst. Wenn nicht, muss der Vorgang erneut wiederholt werden.--[[Benutzer:Unicycle|Unicycle]] 17:48, 26. Jan. 2013 (CET)<br /><br /> |
| + | |||
| + | So könntest du es lösen. Wie müsst man es lösen, wenn AB und CD nicht parallel verlaufen würden?--[[Benutzer:Tutorin Anne|Tutorin Anne]] 13:31, 28. Jan. 2013 (CET) | ||
[[Kategorie:_Einführung_P]] | [[Kategorie:_Einführung_P]] | ||
Aktuelle Version vom 28. Januar 2013, 13:31 Uhr
Nachstehende Abbildung zeigt den Schnitt durch einen Lichtwellenleiter (LWL) und den Weg, den ein Laserstrahl bis zum Punkt P zurücklegt (Pfeile). Das Laserlicht im LWL wird jeweils an den Grenzflächen (Glas, Luft) total reflektiert. Die beiden Grenzgeraden AB und CD können als ideale Spiegel betrachtet werden. Konstruieren Sie nur mit Zirkel und Lineal den weiteren Weg des Lichts vom Punkt P aus bis zur Begrenzungslinie  .
.
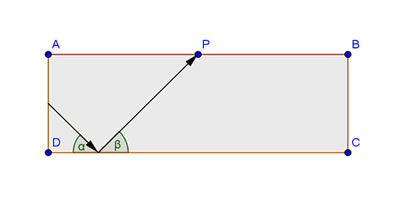
Ich steche in P ein, stelle den Zirkel bis zum Scheitel des Winkels Bete ein, mache einen Bogen um P, sodass ein Schnittpunkt S1 mit der Halbgeraden DC+ entsteht, dann verbinde ich P mit S1. Jetzt steche ich in S1 ein und zeichen einen Bogen um S1 mit dem Radius |SP|, bis ein Schnittpunt S2 mit der Halbgeraden AB+ entsteht. Ich verbinde S1 und S2. Liegt S2 außerhalb der Strecke AB schneidet die Strecke S1S2 BC und die Aufgabe ist gelöst. Wenn nicht, muss der Vorgang erneut wiederholt werden.--Unicycle 17:48, 26. Jan. 2013 (CET)
So könntest du es lösen. Wie müsst man es lösen, wenn AB und CD nicht parallel verlaufen würden?--Tutorin Anne 13:31, 28. Jan. 2013 (CET)

