Lösung von Aufgabe 12.05 WS 12 13: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „<div style="margin:0; margin-right:4px; border:1px solid #27408B; padding: 1em 1em 1em 1em; background-color:#FFFF99; align:left;"> {|width=90%| style="background…“) |
*m.g.* (Diskussion | Beiträge) (→Bemerkung --*m.g.* 16:32, 27. Jan. 2013 (CET)) |
||
| (8 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 3: | Zeile 3: | ||
| valign="top" | | | valign="top" | | ||
| − | + | =Aufgabe 12.05= | |
| − | + | {{Definition|Parallelogramm<br />Ein Parallelogramm ist ein Viereck mit zwei Paaren paralleler Seiten.}} | |
| + | Beweisen Sie ohne Verwendung weiterer aus der Schule bekannten Eigenschaften von Parallelogrammen:<br /> | ||
| + | <math>\overline{ABCD}</math> ist ein Parallelogramm <math>\Leftrightarrow \overline{AB} \tilde= \overline{CD} \wedge \overline{AD} \tilde= \overline{BC}</math>. | ||
=Lösung User ...= | =Lösung User ...= | ||
| − | + | [[Datei:12.05.1.jpg|600px]]<br /><br /> | |
| − | + | --[[Benutzer:Yellow|Yellow]] 11:59, 27. Jan. 2013 (CET)<br /><br /> | |
| + | ==Bemerkung --[[Benutzer:*m.g.*|*m.g.*]] 16:32, 27. Jan. 2013 (CET)== | ||
| + | ''Lange Beweise machen die Behauptung zunichte.'' <sub>Sprichwort unter Mathematikern</sub><br /> | ||
| + | <math>\overline{ABCD}</math> ist ein Parallelogramm <math>\Rightarrow \overline{AB} \tilde= \overline{CD} \wedge \overline{AD} \tilde= \overline{BC}</math>.<br /> | ||
| + | Wählen Sie eine einzige beliebige Diagonale. Diese teilt ein Paar gegenüberliegender Innenwinkel. Betrachten Sie diesbezüglich Wechselwinkelpaare. WSW und fertig ist die Laube.<br /> | ||
| + | Bemerkung: Ich mach das nicht um Sie zu ärgern. Ich möchte dass Sie für die Klausur Ihre Effizienz steigern. | ||
=Lösung User ...= | =Lösung User ...= | ||
Aktuelle Version vom 27. Januar 2013, 16:38 Uhr
Aufgabe 12.05Definition Parallelogramm Beweisen Sie ohne Verwendung weiterer aus der Schule bekannten Eigenschaften von Parallelogrammen: Lösung User ...
Bemerkung --*m.g.* 16:32, 27. Jan. 2013 (CET)Lange Beweise machen die Behauptung zunichte. Sprichwort unter Mathematikern Lösung User ... |
 ist ein Parallelogramm
ist ein Parallelogramm 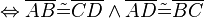 .
.

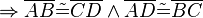 .
.
