Lösung von Zusatzaufgabe 12.2P (WS 12 13): Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(Die Seite wurde neu angelegt: „Beweisen Sie den Innenwinkelsatz für Dreiecke mit Hilfe zweier Punktspiegelungen. <br /> Kategorie:Einführung_P“)
 
 
(5 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt)
Zeile 1: Zeile 1:
 
Beweisen Sie den Innenwinkelsatz für Dreiecke mit Hilfe zweier Punktspiegelungen.
 
Beweisen Sie den Innenwinkelsatz für Dreiecke mit Hilfe zweier Punktspiegelungen.
 
<br />
 
<br />
 +
<br />
 +
<ggb_applet width="900" height="600"  version="4.2" ggbBase64="UEsDBBQACAgIAJoAQ0IAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiu5QIAUEsHCEXM3l0aAAAAGAAAAFBLAwQUAAgICACaAENCAAAAAAAAAAAAAAAADAAAAGdlb2dlYnJhLnhtbO1a2W7bSBZ9Tn9FQQ/zFFO1Lxk5DTtAMAHi7qCTGQzmJaDIssQ2RWpIyksjP5X0f+Sb5lYVSa1eZCdpB5M4drFY6z3nblXS6OfLWY7ObVVnZXE4IBEeIFskZZoVk8PBojk90IOfn/80mthyYsdVjE7LahY3hwMe0cFyHNQiot3gLD0cWBWzRAl2MNZUHnBu4gOjeXJABcZJzGNCDQxGl3X2rCh/iWe2nseJfZtM7Sx+XSZx4+ecNs382XB4cXERdatHZTUZTibj6LJOBwh2XtSHg/bhGUy3NuiC+e4UYzL898nrMP1BVtRNXCR2gJxUi+z5T09GF1mRlhfoIkubKWBgKMgxtdlkCnISzKE2dN3mIO3cJk12bmsYvFL1Ujez+cB3iwvX/iQ8obwXaIDS7DxLbXU4wBHBUimsWf9vgMoqs0XTdibtosNuutF5Zi/CvO7JL8mxUcBCVmfj3B4OTuO8BsGy4rQCUGFH1QKqdXOV23FcdfXlhshT+IEO2R/WzQVyBiQOB5Lgp5SLpwrjp0K0AKwuPEBNWeZ+VoyEQR8+IIopRk9dQUJBoZAyNOHwDrNQ0FDwUIjQh4fhPHTloQ8PfTi7Qc62vhS0fbEmaScnW5WTgHzuV8KvB2BDTr0iJ3FCfEDE7d4XDLl9E79/V/C2KkNV+YLgUJC2Ubs/Hi/5QInYvSQiK6sGfdhn0W5Jog27+5r0QZL2clIsttcEn7JbzgfC20sqVsCFtfx//7u1JNtLzi1jvMeKkj/E+u+xoMJrht9ZfShJW94Ewxfb1GjY+cNRuyFUT13fVqkbO6vdFpnx7gkRJMB8pQJvIhAxUChnxhQRgbiAKtFIulIh5iyXI4Y0cv0IQ94JCQ1/uLdqiQTM5V6qYN6IcSQYIt51cQQoIO/+ABPKoIcQSMAgtzpxyzKJuIQK04jDBp3jU865MBgHdVicIkYQc2OJQlQiSZFyzpNw51OldnuHSSmSGEk3FLwneM7gNWGERsxJA1YwL+usB3dq83nPiscxK+aLpsWufZ/M0g7HptzonpbJ2fEG2Daum+4ZOkHMWobGEMPWIueTUR6PbQ4ZxlunBwidx7kzcz//aVk0qNMBGt5Nqng+zZL6rW0aGFWj3+Pz+HXc2MuX0LvuNuiX9iF9ZBdJnqVZXPwLlMRN4SZEfYT33quL8IaosExSllX69qoG1UGX/7FVCZtiEVcaCywNV5RhsLer0EKJiSQXWFGpFcWKQKiok9jpvCGRUpxrzojEijNoubqmiYSV7XkvWnxpe4HQpMp6Jtzzq/q4zNO+eV5mRfMinjeLyqdrIFTlZDoqJrn12HrfC4lPcjYuL98GUFmY693VHGo4bGA8eVHmZYXAIqkALztpy3EofR+3s74X9n2w74E7lrK0bycuw5u05TiUvhfQHrbWSko6KQnulslq72tg8jWt9ErjsqhFkTWvu0qTJWetqCQM+GUxG4O+tbitz0m+1Jyj4YaKjc5sVdg86FEBXC7KRR00u9fOJ6NFbd/EzfSoSH+zE7DJN7Fziw1MHbout5zaJJvBwPC+BS92xP4TthrepnZS2U7E3GfIAVrfile1euu1n+plVc5eFefvQGs2tjoadvKM6qTK5k450Rj89Jld6l+a1TF4+XR1HAhfgxSJ8zgAZONAHKB40UzLyqfAYLYgD3oJu12AH6EYFNJZbG5nkP2ixqul1+yenhc+r3Y8oHL8O/iRPm6E9iVq0LxTRb0yx/l8Grvcu4Ugj69stQaKn++kTDehAia8POAa5kEn5tYGdQr7hYc5TOetcIVuj32NLiFwRga8jjBKE3igGPzy1eHgAEdMMAl+xXAjGJeKQj7/RziHhTOHA8IZ7pqTDG83OAWVDBjegubR94+mAC8KObWE4w8VnGoV0GSRlAKOClIJDocr4lD+ymAef/9gEhZpLog7i0IOh5U7igY0hVJwttBKGfgr9RcBMylns7hIUeHTwTdlfjUpi8EyEYmxs3cUE6eoKKYO4oDfounawePmENJI6JaEbjEU7HAwDgu2y+xgLyzY8dNPtR6bGkg3zuDcXfsA2rSh0j/8I0tT65Op4c3Ur4C9yj0RzLMvSBs8l+STfci/XkNrO3G1fiPJLTq6/0b31NKlrrGIEcIJI5BTUSZ4q2o0IlwZMFzNpWSGGK9qB1RGRlNBJdES8i0w7s0c4u48gfrkzgheFS7aWh+ftuPzmbVzlxj9Wryr4qJ2l13rgfnuqMePB3UIM86KOVVGCSUJp1x44HUESSg2lDJqhOQ8+EsG3QF3KdwFFXgGyr8j2MePCHYWAbJSYaYpHB84xm2cEpEBneZacGgA/Q4xn8JZg1HOoU1zCoQ9KtTX/fZr2NRupx1veevJzR7ZydezM3lwOP1LDCYSAsiVcJJURisj78+c/W8RhtTh/JHN5nmWZM3NdJxkaUhL1ilJtrg4uTU8riY3J7cZ0246XKYwCcU4FA9nREKOwh22zAgIBlx1gQNjwxj4KUEJRBTzFXKUa8Ad7wD3PdkP3vfk0QBMcKThXMI4FhKDZrcAk8hIwaWQWoI1EKm+RhZ4klVVWW3gexz8yck2zsd/i+dl/fd9oO6G/KXJ+pp/IUIQ8PaQd0N0YEZ150EO2ZFiPiwYON9w/q3wPurwfk+2ED/aH/Gjx4U4gZhrGCSdGOKuAoVmHeCQ52gNvlsxOO1Q8RXg3hEsW+Ve0eQ1vO0eIdPeL+H58jGTRYQJQ5XQgilCRXcqJxycNKYcKw2ppAagQ3Yv3WldEzixU+5/vnXU3MFLawRH1/Byugcvp4+HF2YMuBujNDZGahHunsDhUwoOX0DWIqGUIQsVClIfrOAMJhTEAWW+NSt9zrpBzWmgxm6R8nIft/Ty0QRcxcDLYCmJkEosIwA4qEgKw7S7viJUtx5JuU8buACLAb6YNvoL+if/ccFuB9VewbzYAv3zx5tR99fLParQ242HzSy6LcHJngvMDSaUadA0ddt1yk2hguBtg9nrMmVPBe+u46tkBfvuSi7Py4vf7GluLz2wdz1S7WKhPVMdBxaOtln4tBcLn7ZZENhgSOs0uAgF+R//wcI2C21QeHHddeTnP/di4c9NFsDguXa32UCDYO4LMD9Y2GbBJ6arRFwXpD9/uku2umkaK+nqDwPZN1i04K2ys+Pc9vnjPYj5eB0xG/HD/P8RM1z9rNV/96H9muTz/wFQSwcIbiabUFsJAADWKQAAUEsBAhQAFAAICAgAmgBDQkXM3l0aAAAAGAAAABYAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhX2phdmFzY3JpcHQuanNQSwECFAAUAAgICACaAENCbiabUFsJAADWKQAADAAAAAAAAAAAAAAAAABeAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAACAAIAfgAAAPMJAAAAAA==" showResetIcon = "false" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "true" showMenuBar = "true" showToolBar = "true" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" />
 +
<br />
 +
 +
 +
{| class="wikitable sortable"
 +
! !!
 +
|-
 +
| Voraussetzung || Dreieck ABC mit den Innenwinkeln <math>\alpha ,\beta ,\gamma</math>
 +
|-
 +
| Behauptung || <math>\left| \alpha  \right| +\left| \beta  \right| +\left| \gamma  \right| = 180</math>
 +
|}
 +
 +
<br />
 +
{| class="wikitable sortable"
 +
!Beweisschritte!!Begründung!! Hinweis (Tutorin_Anne)!!Änderungsvorschläge
 +
|-
 +
|1. Wir konstruieren eine Gerade g, für die gilt g ll <math>\overline{AB}</math> ^ C<math>\in</math>g    ||  Parallelenaxiom, Vor.
 +
|-
 +
|2. D(mb,180)(A)=C ^ D(mb,180)(B)=B' ||1.), Def. Punktspiegelung, Def. Mittelpunkt
 +
|-
 +
|2.1 <math>B'C \equiv g</math>  ||1.),2.) || Warum folgt das aus Schritt 1 und 2? || Man müsste vllt. noch Satz IX.4 <span style="color: red">(richtig! Parallelentreue der Punktspiegelung)</span>erwähnen, sodass gilt AB parallel C'B und laut Parallelenaxiom <span style="color: red">(genau!)</span>gibt es nur eine parallele Gerade durch C, heißt B'C muss auf g zu liegen kommen.
 +
|-
 +
|3. <math>\alpha \tilde {=}\alpha '</math> || Wechselwinkelsatz, 1.),2.),2.1), Eig. Punktspiegelung (winkeltreue), winkelmaßerhaltend || Das sind zu viele Begründungen, entscheide dich! || Eig. Punktspiegelung (winkeltreue), 2.1),2.)
 +
|-
 +
|4. D(ma,180)(A)=A' ^D(ma,180)(B)=C || 1.), Def. Punktspiegelung, Def. Mittelpunkt
 +
|-
 +
|5. <math>\beta \tilde {=} \beta'</math> || 4.),2.1) Wechselwinkelsatz, Eig. Punktspiegelung (winkeltreue), winkelmaßerhaltend ||Das sind zu viele Begründungen, entscheide dich! || Eig. Punktspiegelung (winkeltreue), 2.1),4.) <span style="color: red">(gut!)</span>
 +
|-
 +
|6. <math>\left| \alpha'  \right| + \left| \beta' \right|+ \left| \gamma  \right|= 180</math> || 4.), 5.),Def. Nebenwinkel, Satz(Nebenwinkel sind supplementär)|| Woher weißt du, dass sie alle an einer Geraden liegen?|| Die Winkel alpha',beta',gamma' besitzen alle den gleichen Scheitelpunkt, nämlich C. Das ist anzunehmen, da der Winkel alpha mit dem Scheitelpunkt A punktgespiegelt wird und alpha' nun den Scheitelpunkt C hat.(Für B analog). Der Winkel Gamma hat ja schon den Scheitelpunkt C. <span style="color: red"> Die Voraussetzung ist ja, dass B´, C, A´ auf einer Geraden liegen, daher würde ich eher noch einen Schritt für A'C = g wie 2.1 einfügen. -Tutorin_Anne</span>
 +
|-
 +
|7. <math>\left| \alpha  \right| + \left| \beta \right|+ \left| \gamma  \right|= 180</math> || 3.),5.),6.)
 +
|}
 +
<br />--[[Benutzer:TobiWan|TobiWan]] 00:37, 3. Feb. 2013 (CET)<br />
 +
* Im Großen und Ganzen stimmt der Beweis. Ich habe ein paar Kleinigkeiten angemerkt.--[[Benutzer:Tutorin Anne|Tutorin Anne]] 17:49, 5. Feb. 2013 (CET)
 +
 +
<br />--[[Benutzer:TobiWan|TobiWan]] 11:52, 6. Feb. 2013 (CET)
 +
Eingefügt in rot.--[[Benutzer:Tutorin Anne|Tutorin Anne]] 14:07, 6. Feb. 2013 (CET)
 
[[Kategorie:Einführung_P]]
 
[[Kategorie:Einführung_P]]

Aktuelle Version vom 6. Februar 2013, 14:07 Uhr

Beweisen Sie den Innenwinkelsatz für Dreiecke mit Hilfe zweier Punktspiegelungen.



Voraussetzung Dreieck ABC mit den Innenwinkeln 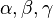\alpha ,\beta ,\gamma
Behauptung 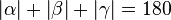\left| \alpha \right| +\left| \beta \right| +\left| \gamma \right| = 180


Beweisschritte Begründung Hinweis (Tutorin_Anne) Änderungsvorschläge
1. Wir konstruieren eine Gerade g, für die gilt g ll \overline{AB} ^ C\ing Parallelenaxiom, Vor.
2. D(mb,180)(A)=C ^ D(mb,180)(B)=B' 1.), Def. Punktspiegelung, Def. Mittelpunkt
2.1 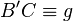B'C \equiv g 1.),2.) Warum folgt das aus Schritt 1 und 2? Man müsste vllt. noch Satz IX.4 (richtig! Parallelentreue der Punktspiegelung)erwähnen, sodass gilt AB parallel C'B und laut Parallelenaxiom (genau!)gibt es nur eine parallele Gerade durch C, heißt B'C muss auf g zu liegen kommen.
3. 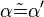\alpha \tilde {=}\alpha ' Wechselwinkelsatz, 1.),2.),2.1), Eig. Punktspiegelung (winkeltreue), winkelmaßerhaltend Das sind zu viele Begründungen, entscheide dich! Eig. Punktspiegelung (winkeltreue), 2.1),2.)
4. D(ma,180)(A)=A' ^D(ma,180)(B)=C 1.), Def. Punktspiegelung, Def. Mittelpunkt
5. 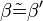\beta \tilde {=} \beta' 4.),2.1) Wechselwinkelsatz, Eig. Punktspiegelung (winkeltreue), winkelmaßerhaltend Das sind zu viele Begründungen, entscheide dich! Eig. Punktspiegelung (winkeltreue), 2.1),4.) (gut!)
6. 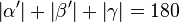\left| \alpha' \right| + \left| \beta' \right|+ \left| \gamma \right|= 180 4.), 5.),Def. Nebenwinkel, Satz(Nebenwinkel sind supplementär) Woher weißt du, dass sie alle an einer Geraden liegen? Die Winkel alpha',beta',gamma' besitzen alle den gleichen Scheitelpunkt, nämlich C. Das ist anzunehmen, da der Winkel alpha mit dem Scheitelpunkt A punktgespiegelt wird und alpha' nun den Scheitelpunkt C hat.(Für B analog). Der Winkel Gamma hat ja schon den Scheitelpunkt C. Die Voraussetzung ist ja, dass B´, C, A´ auf einer Geraden liegen, daher würde ich eher noch einen Schritt für A'C = g wie 2.1 einfügen. -Tutorin_Anne
7. 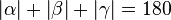\left| \alpha \right| + \left| \beta \right|+ \left| \gamma \right|= 180 3.),5.),6.)


--TobiWan 00:37, 3. Feb. 2013 (CET)

  • Im Großen und Ganzen stimmt der Beweis. Ich habe ein paar Kleinigkeiten angemerkt.--Tutorin Anne 17:49, 5. Feb. 2013 (CET)


--TobiWan 11:52, 6. Feb. 2013 (CET) Eingefügt in rot.--Tutorin Anne 14:07, 6. Feb. 2013 (CET)

Von „http://geometrie.zum.de/index.php?title=Lösung_von_Zusatzaufgabe_12.2P_(WS_12_13)&oldid=21618“