Probeklausur WS 12 13 Aufgabe 1: Unterschied zwischen den Versionen
Monron (Diskussion | Beiträge) (→Lösung User ...) |
*m.g.* (Diskussion | Beiträge) (→Lösung User --Sweetnightmare5 19:27, 5. Feb. 2013 (CET)) |
||
| (27 dazwischenliegende Versionen von 8 Benutzern werden nicht angezeigt) | |||
| Zeile 10: | Zeile 10: | ||
==Lösung User Ron== | ==Lösung User Ron== | ||
{P/ Zw (A,P,B)} U {A,B} | {P/ Zw (A,P,B)} U {A,B} | ||
| + | ===Bewertung=== | ||
| + | 2 von 2 Punkten | ||
==Lösung User ...== | ==Lösung User ...== | ||
| Zeile 20: | Zeile 22: | ||
Eine Menge von Punkten heißt komplanar, wenn es eine Ebene gibt, die alle Punkte der Menge enthält. | Eine Menge von Punkten heißt komplanar, wenn es eine Ebene gibt, die alle Punkte der Menge enthält. | ||
| + | ===Bewertung=== | ||
| + | 1 von 2 Punkten --[[Benutzer:*m.g.*|*m.g.*]] 18:01, 4. Feb. 2013 (CET) | ||
| + | |||
| + | Vier Punkte heißen komplanar, wenn sie in ein und derselben Ebene liegen.--[[Benutzer:Caro44|Caro44]] 20:01, 4. Feb. 2013 (CET) | ||
| + | |||
| + | Vier Punkte A, B, C, und D sind komplanar, wenn es eine Ebene gibt, die alle diese Punkte enthält. --[[Benutzer:...lw)...|...lw)...]] 10:45, 5. Feb. 2013 (CET) | ||
==Lösung User ...== | ==Lösung User ...== | ||
| + | <br /> | ||
| + | Drei Punkte heißen komplanar, wenn es ein Ebene gibt, die alle Punkte A,B,C enthällt.<br /> | ||
| + | komp(A,B,C)<br /> | ||
| + | (AxiomI/4)<br />--[[Benutzer:B.....|B.....]] 14:08, 5. Feb. 2013 (CET) | ||
| + | |||
| + | ===Bemerkung --[[Benutzer:*m.g.*|*m.g.*]] 23:18, 9. Feb. 2013 (CET)=== | ||
| + | Gerade wegen Axiom I/4, welches ja aussagt, dass drei Punkte immer komplanar sind, macht die Definition erst ab 4 Punkten so richtig Sinn. | ||
| + | |||
| + | Analogie: Sehnendreieck, Sehnenviereck. | ||
=Aufgabe c= | =Aufgabe c= | ||
| Zeile 29: | Zeile 46: | ||
Ein Viereck ist eine Raute, wenn alle vier Seiten gleich lang sind. | Ein Viereck ist eine Raute, wenn alle vier Seiten gleich lang sind. | ||
| + | ===Bewertung=== | ||
| + | 2 von 2 Punkten--[[Benutzer:*m.g.*|*m.g.*]] 18:02, 4. Feb. 2013 (CET) | ||
| + | |||
| + | === Lösung ...lw)... === | ||
| + | Eine Raute ist ein Viereck mit zwei Paar paralleler und 3 gleichlangen Seiten. --[[Benutzer:...lw)...|...lw)...]] 10:46, 5. Feb. 2013 (CET) | ||
==Lösung User Ron== | ==Lösung User Ron== | ||
Wenn ein Viereck eine Raute ist, dann sind alle vier Seiten des Vierecks gleich lang. | Wenn ein Viereck eine Raute ist, dann sind alle vier Seiten des Vierecks gleich lang. | ||
| + | ===Bewertung=== | ||
| + | 0 von 2 Punkten--[[Benutzer:*m.g.*|*m.g.*]] 18:03, 4. Feb. 2013 (CET) | ||
=Aufgabe d= | =Aufgabe d= | ||
| Zeile 40: | Zeile 64: | ||
==Lösung User Ron== | ==Lösung User Ron== | ||
| − | Ein Kriterium | + | Ein Kriterium<br /> |
| + | <br /> Frage dazu: Wenn es ein Kriterium ist, kann man dann auch sagen, dass es notwendig und hinreichend ist?--[[Benutzer:B.....|B.....]] 20:20, 5. Feb. 2013 (CET) | ||
| + | ===Bewertung=== | ||
| + | 2 von 2 Punkten | ||
| + | <br /> | ||
| + | Warum ist das ein Kriterium?--[[Benutzer:Natürliches Mineralwasser|Natürliches Mineralwasser]] 20:52, 9. Feb. 2013 (CET)<br /> | ||
| + | ==Lösung User --[[Benutzer:Sweetnightmare5|Sweetnightmare5]] 19:27, 5. Feb. 2013 (CET)== | ||
| + | |||
| + | Hinreichende Bedingung | ||
| + | |||
| + | --[[Benutzer:Dothewave|Dothewave]] 22:06, 9. Feb. 2013 (CET)-- Dothewave | ||
| + | Also ich glaube auch, dass es eine hinreichende Bedingung ist. Begründung: Die Eigenschaft E1 ist nicht zwingend erforderlich, um den Begriff B zu definieren. Es könnte auch eine andere Eigenschaft verwednet werden. | ||
| + | Ein Kriterium sagt aus, dass GENAU DANN wenn die Eigenschaft auftriff die Bedingung erfüllt ist. Dort ist sie hinreichent und auch notwenig zugleich und daher nicht austauschbar. | ||
| + | Also soweit mein Verständnig, wenn jemand mehr weiß,wäre auch ich dankbar um die richtige Antwort. | ||
| + | ===Bemerkungen--[[Benutzer:*m.g.*|*m.g.*]] 00:16, 10. Feb. 2013 (CET)=== | ||
| + | Meine Bewertung: 1 von 2 Punkten<br /> | ||
| + | |||
| + | Warum nicht die volle Punktzahl? Es ist sicherlich richtig, dass <math>E_1</math> eine notwendige Bedingung hinsichtlich der Entscheidung, ob irgend ein Repräsentant zu <math>B</math> gehört. Das ist aber nur die halbe Wahrheit. Weil der Begriff über <math>E_1</math> definiert wurde, <math>E_1</math> also definierende Eigenschaft ist, ist <math>E_1</math> auch eine notwendige Bedingung hinsichtlich der Entscheidung ob ein gewisses Objekt Repräsentant von <math>B</math> ist. | ||
| + | |||
| + | Definierende Eigenschaften müssen immer notwendig und hinreichend und somit Kriterien sein. | ||
| + | |||
| + | |||
| + | Beispiel: Wir haben einen Sack voller Vierecke und wollen alle die aussortieren, die Parallelogramme sind. Frisch machen wir uns ans Werk und messen die Seitenlängen. Dann sortieren wir alle Vierecke aus, deren vier Seiten ein und dieselbe Länge haben. Im aussortieren Viereckshaufen liegen auf jeden Fall nur Parallelogramme. Die Eigenschaft eines Vierecks, dass alle seine Seiten zueinander kongruent sind, ist also hinreichen dafür dass wir zielsicher nur Parallelogramme aussortiert haben. Wäre es jetzt korrekt zu definieren: ''Wenn in einem Viereck alle Seiten zueinander kongruent sind, dann ist es ein Parallelogramm?'' | ||
| + | |||
| + | Offenbar nicht, denn wir haben nur Rauten aussortiert. Diese sind Parallelogramme, jedoch sehr spezifische. Ein Großteil der Parallelogramme ist uns ''entwischt''. | ||
| + | |||
| + | Oh, vielleicht ist es ja gar nicht notwendig so viel zu messen. Vielleicht reicht es ja aus, nur ein Paar gegenüberliegender Seiten zu messen. Das halbiert unseren Aufwand. Frisch machen wir uns wieder ans Werk. Auf unserem aussortierten Haufen liegen jetzt wieder alle Rauten und nicht nur die alle beliebigen Parallelogramme auch. Auch der Spezialfall Rechteck ist dabei. Zu unserem Entsetzen stellen wir jetzt jedoch fest, dass unser Verfahren nicht trennscharf genug ist. Neben allen Parallelogrammen haben wir quasi als Beifang auch die gleichschenkligen Trapeze dabei, die keine Parallelogramme sind. Ziemlich unökologisch das Ganze. Neben den Thunfischen (die man eigentlich auch nicht mehr fangen sollte) haben wir auch Delfine im Netz. Es ist zwar notwendig, für ein Viereck ein Paar gegenüberliegender zu einander kongruente Seiten zu haben, um zum Parallelogramm zu avancieren, hinreichend (ausreichend) ist diese Eigenschaft jedoch nicht. Um den Begriff sauber zu definieren brauchen wir also eine Bedingung, die sowohl hinreichend als auch notwenig ist. Anders ausgedrückt: Wir brauchen ein Kriterium. | ||
| + | |||
| + | |||
| + | Ein solches haben wir auch gleich parat: Unsere Vierecke sollen zwei Paare von sich gegenüberliegenden Seiten haben, die jeweils zueinander kongruent sind. Das Ganze ist leider etwa aufwendiger als die anderen beiden Methoden, jedoch haben wir jetzt zielsicher '''alle''' Parallelogramme unserer Ausgangsmenge aussortiert. | ||
| + | |||
| + | Wir melden unsere Methode zum Patent an und lassen offiziell verkünden, dass Alle Vierecke mit zwei Paaren einander gegenüberliegender Seiten, die jeweils kongruent zueinander sind, ab heute Parallelogramme heißen. | ||
| + | |||
| + | Schön und gut, es dauert nicht lange bis uns eine Mitteilung aus der Parallelwelt erreicht: bei uns sind die und nur die Vierecke Parallelogramme, die zwei Paare zueinander paralleler Seiten haben. Vor einigen Jahren hätte uns diese Mitteilung kalt gelassen. Es ist nun jedoch politischer Wille von ganz oben und in Brüssel, die Parallelwelt in Europa aufzunehmen. Die politischen Vertreter der Parallelwelt haben bereits offiziell erklärt, dass Sie auf keinen Fall davon abrücken werden, unter Parallelogrammen Vierecke mit zwei Paaren zueinander paralleler Seiten zu verstehen. Das ist eine nationale Besonderheit und schon weil das Parallelogramm seit Urzeiten das Staatswappen der Parallelwelt ist, wir man diesbezüglich keine Kompromisse eingehen. Die EU könne ja auch ihre Definition der der Parallelwelt anpassen. | ||
| + | |||
| + | Also die Bildzeitung eines Tages nicht recht weiß, was zu berichten wäre(Frau Elvers-Elbertzhagen trinkt wieder, aber das interessiert schon lange keine Sau mehr) bringt sie die Schlagzeile: Parallelwelt erpresst EU mit Parallelogrammdefinition, wieviel Parallelogramm dürfen wir noch sein? | ||
| + | |||
| + | Verhindern Sie rechtsradikale Aufmärsche und schreiben Sie die Story zu einem guten Ende weiter ... --[[Benutzer:*m.g.*|*m.g.*]] 00:16, 10. Feb. 2013 (CET) | ||
| + | |||
| + | =Aufgabe a= | ||
| + | Es seien <math>A</math> und <math>B</math> zwei verschiedene Punkte.<br /> Ergänzen Sie <math>\overline{AB}:= \ldots</math> . | ||
| + | ==Lösung User Ron== | ||
| + | {P/ Zw (A,P,B)} U {A,B} | ||
| + | ===Bewertung=== | ||
| + | 2 von 2 Punkten | ||
| + | |||
| + | ==Lösung User ...== | ||
| + | |||
| + | |||
| + | =Aufgabe b= | ||
| + | Definieren Sie den Begriff ''komplanar'' für die Anzahl von Punkten, ab der der Begriff sinnvoll ist. | ||
| + | |||
| + | ==Lösung User ...== | ||
| + | |||
| + | Eine Menge von Punkten heißt komplanar, wenn es eine Ebene gibt, die alle Punkte der Menge enthält. | ||
| + | ===Bewertung=== | ||
| + | 1 von 2 Punkten --[[Benutzer:*m.g.*|*m.g.*]] 18:01, 4. Feb. 2013 (CET) | ||
| + | |||
| + | Vier Punkte heißen komplanar, wenn sie in ein und derselben Ebene liegen.--[[Benutzer:Caro44|Caro44]] 20:01, 4. Feb. 2013 (CET) | ||
| + | |||
| + | Vier Punkte A, B, C, und D sind komplanar, wenn es eine Ebene gibt, die alle diese Punkte enthält. --[[Benutzer:...lw)...|...lw)...]] 10:45, 5. Feb. 2013 (CET) | ||
| + | |||
| + | ==Lösung User ...== | ||
| + | <br /> | ||
| + | Drei Punkte heißen komplanar, wenn es ein Ebene gibt, die alle Punkte A,B,C enthällt.<br /> | ||
| + | komp(A,B,C)<br /> | ||
| + | (AxiomI/4)<br />--[[Benutzer:B.....|B.....]] 14:08, 5. Feb. 2013 (CET) | ||
| + | |||
| + | ===Bemerkung --[[Benutzer:*m.g.*|*m.g.*]] 23:18, 9. Feb. 2013 (CET)=== | ||
| + | Gerade wegen Axiom I/4, welches ja aussagt, dass drei Punkte immer komplanar sind, macht die Definition erst ab 4 Punkten so richtig Sinn. | ||
| + | |||
| + | Analogie: Sehnendreieck, Sehnenviereck. | ||
| + | |||
| + | =Aufgabe c= | ||
| + | Definieren Sie den Begriff ''Raute'' unter Verwendung des Oberbegriffs ''Viereck''. | ||
| + | |||
| + | ==Lösung User Ron== | ||
| + | |||
| + | Ein Viereck ist eine Raute, wenn alle vier Seiten gleich lang sind. | ||
| + | ===Bewertung=== | ||
| + | 2 von 2 Punkten--[[Benutzer:*m.g.*|*m.g.*]] 18:02, 4. Feb. 2013 (CET) | ||
| + | |||
| + | === Lösung ...lw)... === | ||
| + | Eine Raute ist ein Viereck mit zwei Paar paralleler und 3 gleichlangen Seiten. --[[Benutzer:...lw)...|...lw)...]] 10:46, 5. Feb. 2013 (CET) | ||
| + | |||
| + | ==Lösung User Ron== | ||
| + | |||
| + | Wenn ein Viereck eine Raute ist, dann sind alle vier Seiten des Vierecks gleich lang. | ||
| + | ===Bewertung=== | ||
| + | 0 von 2 Punkten--[[Benutzer:*m.g.*|*m.g.*]] 18:03, 4. Feb. 2013 (CET) | ||
| + | |||
| + | =Aufgabe d= | ||
| + | Nur unter Verwendung der Eigenschaft <math>E_1</math> sei der Begriff <math>B</math> korrekt definiert. Es stellt sich heraus, dass <math>B</math> ebenso korrekt über die Eigenschaft <math>E_2</math> hätte definiert werden können.<br /> Was ist <math>E_1</math> hinsichtlich einer Entscheidung, ob ein Repräsentant <math>R</math> zum Begriff <math>B</math> gehört? | ||
| + | |||
| + | |||
| + | ==Lösung User Ron== | ||
| + | |||
| + | Ein Kriterium<br /> | ||
| + | <br /> Frage dazu: Wenn es ein Kriterium ist, kann man dann auch sagen, dass es notwendig und hinreichend ist?--[[Benutzer:B.....|B.....]] 20:20, 5. Feb. 2013 (CET) | ||
| + | ===Bewertung=== | ||
| + | 2 von 2 Punkten | ||
| + | <br /> | ||
| + | Warum ist das ein Kriterium?--[[Benutzer:Natürliches Mineralwasser|Natürliches Mineralwasser]] 20:52, 9. Feb. 2013 (CET)<br /> | ||
| + | ==Lösung User --[[Benutzer:Sweetnightmare5|Sweetnightmare5]] 19:27, 5. Feb. 2013 (CET)== | ||
| + | |||
| + | Hinreichende Bedingung | ||
| + | |||
| + | --[[Benutzer:Dothewave|Dothewave]] 22:06, 9. Feb. 2013 (CET)-- Dothewave | ||
| + | Also ich glaube auch, dass es eine hinreichende Bedingung ist. Begründung: Die Eigenschaft E1 ist nicht zwingend erforderlich, um den Begriff B zu definieren. Es könnte auch eine andere Eigenschaft verwednet werden. | ||
| + | Ein Kriterium sagt aus, dass GENAU DANN wenn die Eigenschaft auftriff die Bedingung erfüllt ist. Dort ist sie hinreichent und auch notwenig zugleich und daher nicht austauschbar. | ||
| + | Also soweit mein Verständnig, wenn jemand mehr weiß,wäre auch ich dankbar um die richtige Antwort. | ||
| + | |||
| + | |||
| + | |||
| + | ===Bewertung=== | ||
| + | Meine Bewertung: 1 von 2 Punkten<br /> | ||
| + | Warum nicht die volle Punktzahl? Es ist sicherlich richtig, dass <math>E_1</math> eine notwendige Bedingung hinsichtlich der Entscheidung, ob irgend ein Repräsentant zu <math>B</math> gehört. Das ist aber nur die halbe Wahrheit. Weil der Begriff über <math>E_1</math> definiert wurde, <math>E_1</math> also definierende Eigenschaft ist, ist <math>E_1</math> auch eine notwendige Bedingung hinsichtlich der Entscheidung ob ein gewisses Objekt Repräsentant von <math>B</math> ist. | ||
| + | |||
| + | Definierende Eigenschaften müssen immer notwendig und hinreichend und somit Kriterien sein. | ||
| + | |||
| + | |||
| + | Beispiel: Wir haben einen Sack voller Vierecke und wollen alle die aussortieren, die Parallelogramme sind. Frisch machen wir uns ans Werk und messen die Seitenlängen. Dann sortieren wir alle Vierecke aus, deren vier Seiten ein und dieselbe Länge haben. Im aussortieren Viereckshaufen liegen auf jeden Fall nur Parallelogramme. Die Eigenschaft eines Vierecks, dass alle seine Seiten zueinander kongruent sind, ist also hinreichen dafür dass wir zielsicher nur Parallelogramme aussortiert haben. Wäre es jetzt korrekt zu definieren: ''Wenn in einem Viereck alle Seiten zueinander kongruent sind, dann ist es ein Parallelogramm?'' | ||
| + | |||
| + | Offenbar nicht, denn wir haben nur Rauten aussortiert. Diese sind Parallelogramme, jedoch sehr spezifische. Ein Großteil der Parallelogramme ist uns ''entwischt''. | ||
| + | |||
| + | Oh, vielleicht ist es ja gar nicht notwendig so viel zu messen. Vielleicht reicht es ja aus, nur ein Paar gegenüberliegender Seiten zu messen. Das halbiert unseren Aufwand. Frisch machen wir uns wieder ans Werk. Auf unserem aussortierten Haufen liegen jetzt wieder alle Rauten und nicht nur die alle beliebigen Parallelogramme auch. Auch der Spezialfall Rechteck ist dabei. Zu unserem Entsetzen stellen wir jetzt jedoch fest, dass unser Verfahren nicht trennscharf genug ist. Neben allen Parallelogrammen haben wir quasi als Beifang auch die gleichschenkligen Trapeze dabei, die keine Parallelogramme sind. Ziemlich unökologisch das Ganze. Neben den Thunfischen (die man eigentlich auch nicht mehr fangen sollte) haben wir auch Delfine im Netz. Es ist zwar notwendig, für ein Viereck ein Paar gegenüberliegender zu einander kongruente Seiten zu haben, um zum Parallelogramm zu avancieren, hinreichend (ausreichend) ist diese Eigenschaft jedoch nicht. Um den Begriff sauber zu definieren brauchen wir also eine Bedingung, die sowohl hinreichend als auch notwenig ist. Anders ausgedrückt: Wir brauchen ein Kriterium. | ||
| + | |||
| + | |||
| + | Ein solches haben wir auch gleich parat: Unsere Vierecke sollen zwei Paare von sich gegenüberliegenden Seiten haben, die jeweils zueinander kongruent sind. Das Ganze ist leider etwa aufwendiger als die anderen beiden Methoden, jedoch haben wir jetzt zielsicher '''alle''' Parallelogramme unserer Ausgangsmenge aussortiert. | ||
| + | |||
| + | Wir melden unsere Methode zum Patent an und lassen offiziell verkünden, dass Alle Vierecke mit zwei Paaren einander gegenüberliegender Seiten, die jeweils kongruent zueinander sind, ab heute Parallelogramme heißen. | ||
| + | |||
| + | Schön und gut, es dauert nicht lange bis uns eine Mitteilung aus der Parallelwelt erreicht: bei uns sind die und nur die Vierecke Parallelogramme, die zwei Paare zueinander paralleler Seiten haben. Vor einigen Jahren hätte uns diese Mitteilung kalt gelassen. Es ist nun jedoch politischer Wille von ganz oben und in Brüssel, die Parallelwelt in Europa aufzunehmen. Die politischen Vertreter der Parallelwelt haben bereits offiziell erklärt, dass Sie auf keinen Fall davon abrücken werden, unter Parallelogrammen Vierecke mit zwei Paaren zueinander paralleler Seiten zu verstehen. Das ist eine nationale Besonderheit und schon weil das Parallelogramm seit Urzeiten das Staatswappen der Parallelwelt ist, wir man diesbezüglich keine Kompromisse eingehen. Die EU könne ja auch ihre Definition der der Parallelwelt anpassen. | ||
| + | |||
| + | Also die Bildzeitung eines Tages nicht recht weiß, was zu berichten wäre(Frau Elvers-Elbertzhagen trinkt wieder, aber das interessiert schon lange keine Sau mehr) bringt sie die Schlagzeile: Parallelwelt erpresst EU mit Parallelogrammdefinition, wieviel Parallelogramm dürfen wir noch sein? | ||
| + | |||
| + | Verhindern Sie rechtsradikale Aufmärsche und schreiben Sie die Story zu einem guten Ende weiter ... --[[Benutzer:*m.g.*|*m.g.*]] 00:14, 10. Feb. 2013 (CET) | ||
==Lösung User ...== | ==Lösung User ...== | ||
| Zeile 47: | Zeile 207: | ||
Es sei <math>R</math> ein beliebiger Punkt und <math>r \in \mathbb{R}, r>0</math>. Was ist das? <math>M:=\left\{P||RP|\leq r \right\}</math>. | Es sei <math>R</math> ein beliebiger Punkt und <math>r \in \mathbb{R}, r>0</math>. Was ist das? <math>M:=\left\{P||RP|\leq r \right\}</math>. | ||
| + | <br /><br /> | ||
| + | Die Punktmenge M ist das Volumen einer Kugel mit Mittelpunkt R und Radius r.--[[Benutzer:Natürliches Mineralwasser|Natürliches Mineralwasser]] 20:50, 9. Feb. 2013 (CET)<br /><br /> | ||
| + | ==Lösung User ...== | ||
| + | Eine Kugel | ||
| + | ===Bewertung=== | ||
| + | 1 von 2 Punkten--[[Benutzer:*m.g.*|*m.g.*]] 18:04, 4. Feb. 2013 (CET) | ||
| + | |||
| + | ==Lösung User Aaliyah== | ||
| + | |||
| + | Es ist eine Kugel um P mit dem Radius r inklusive ihres Inneren.--[[Benutzer:Aaliyah|Aaliyah]] 18:55, 4. Feb. 2013 (CET) | ||
| + | |||
| + | |||
| + | |||
| + | === Lösung User ...lw)... === | ||
| + | M ist eine Kugel mit dem Radius RP. --[[Benutzer:...lw)...|...lw)...]] 10:50, 5. Feb. 2013 (CET) | ||
| + | |||
| + | =Aufgabe f= | ||
| + | Definieren Sie den Begriff ''Rechter Winkel'' wie in der Vorlesung. | ||
| + | |||
| + | |||
| + | ==Lösung User Ron== | ||
| + | |||
| + | Ein Winkel, der so groß ist, wie einer seiner Nebenwinkel, nennt man rechter Winkel. | ||
| + | |||
| + | ===Bewertung=== | ||
| + | 2 von 2 Punkten mit sehr großen Bauchschmerzen:<br /> | ||
| + | Wen oder was nennt man rechter Winkel? Ein'''en''' Winkel, der ...--[[Benutzer:*m.g.*|*m.g.*]] 18:06, 4. Feb. 2013 (CET) | ||
| + | |||
| + | ==Lösung User Aaliyah== | ||
| + | |||
| + | Wenn ein Winkel so groß ist, wie einer seiner Nebenwinkel, dann ist der Winkel ein Rechter.--[[Benutzer:Aaliyah|Aaliyah]] 18:57, 4. Feb. 2013 (CET) | ||
| + | |||
| + | =Aufgabe g= | ||
| + | Ergänzen Sie die folgende Definition: Zwei Geraden <math>a</math> und <math>b</math> sind windschief, wenn <math>\ldots</math> | ||
| + | |||
| + | |||
| + | ==Lösung User Ron== | ||
| + | |||
| + | ,wenn sie nicht parallel sind und keinen gemeinsamen Schnittpunkt(schnittfrei sind) haben | ||
| + | ===Bewertung=== | ||
| + | 2 von 2 Punkten, besser ''schnittpunktfrei'' --[[Benutzer:*m.g.*|*m.g.*]] 18:08, 4. Feb. 2013 (CET) | ||
==Lösung User ...== | ==Lösung User ...== | ||
| − | Eine Kugel | + | |
| + | =Aufgabe h= | ||
| + | Definieren Sie den Begriff Tangentialebene einer Kugel. | ||
| + | |||
| + | |||
| + | ==Lösung User Ron== | ||
| + | |||
| + | Eine Ebene, welche eine Kugel in einem Punkt berührt, nennt man Tangentialebene | ||
| + | |||
| + | ===Bewertung=== | ||
| + | 1 von 2 Punkten--[[Benutzer:*m.g.*|*m.g.*]] 18:10, 4. Feb. 2013 (CET)<br /> | ||
| + | Tangentialebene sein ist eine zweistellige Relation, es macht erst Sinn, wenn man formuliert ''Tangentialebene der ...'' | ||
| + | |||
| + | ==Lösung User Aaliyah== | ||
| + | |||
| + | Es sei k eine Kugel. Eine Ebene E, die mit der Kugel k genau einen Berührpunkt B hat, nennt man Tangentialebene an der Kugel k.--[[Benutzer:Aaliyah|Aaliyah]] 19:00, 4. Feb. 2013 (CET) | ||
| + | |||
| + | |||
| + | <!--- Was hier drunter steht muss stehen bleiben ---> | ||
| + | |} | ||
| + | </div> | ||
| + | [[Kategorie:Einführung_S]] | ||
==Lösung User ...== | ==Lösung User ...== | ||
| + | |||
| + | =Aufgabe e= | ||
| + | |||
| + | Es sei <math>R</math> ein beliebiger Punkt und <math>r \in \mathbb{R}, r>0</math>. Was ist das? <math>M:=\left\{P||RP|\leq r \right\}</math>. | ||
| + | <br /><br /> | ||
| + | Die Punktmenge M ist das Volumen einer Kugel mit Mittelpunkt R und Radius r.--[[Benutzer:Natürliches Mineralwasser|Natürliches Mineralwasser]] 20:50, 9. Feb. 2013 (CET)<br /><br /> | ||
| + | ==Lösung User ...== | ||
| + | |||
| + | Eine Kugel | ||
| + | ===Bewertung=== | ||
| + | 1 von 2 Punkten--[[Benutzer:*m.g.*|*m.g.*]] 18:04, 4. Feb. 2013 (CET) | ||
| + | |||
| + | ==Lösung User Aaliyah== | ||
| + | |||
| + | Es ist eine Kugel um P mit dem Radius r inklusive ihres Inneren.--[[Benutzer:Aaliyah|Aaliyah]] 18:55, 4. Feb. 2013 (CET) | ||
| + | |||
| + | |||
| + | |||
| + | === Lösung User ...lw)... === | ||
| + | M ist eine Kugel mit dem Radius RP. --[[Benutzer:...lw)...|...lw)...]] 10:50, 5. Feb. 2013 (CET) | ||
=Aufgabe f= | =Aufgabe f= | ||
| Zeile 63: | Zeile 305: | ||
Ein Winkel, der so groß ist, wie einer seiner Nebenwinkel, nennt man rechter Winkel. | Ein Winkel, der so groß ist, wie einer seiner Nebenwinkel, nennt man rechter Winkel. | ||
| − | == | + | ===Bewertung=== |
| + | 2 von 2 Punkten mit sehr großen Bauchschmerzen:<br /> | ||
| + | Wen oder was nennt man rechter Winkel? Ein'''en''' Winkel, der ...--[[Benutzer:*m.g.*|*m.g.*]] 18:06, 4. Feb. 2013 (CET) | ||
| + | |||
| + | ==Lösung User Aaliyah== | ||
| + | Wenn ein Winkel so groß ist, wie einer seiner Nebenwinkel, dann ist der Winkel ein Rechter.--[[Benutzer:Aaliyah|Aaliyah]] 18:57, 4. Feb. 2013 (CET) | ||
=Aufgabe g= | =Aufgabe g= | ||
| Zeile 73: | Zeile 320: | ||
,wenn sie nicht parallel sind und keinen gemeinsamen Schnittpunkt(schnittfrei sind) haben | ,wenn sie nicht parallel sind und keinen gemeinsamen Schnittpunkt(schnittfrei sind) haben | ||
| + | ===Bewertung=== | ||
| + | 2 von 2 Punkten, besser ''schnittpunktfrei'' --[[Benutzer:*m.g.*|*m.g.*]] 18:08, 4. Feb. 2013 (CET) | ||
==Lösung User ...== | ==Lösung User ...== | ||
| Zeile 85: | Zeile 334: | ||
Eine Ebene, welche eine Kugel in einem Punkt berührt, nennt man Tangentialebene | Eine Ebene, welche eine Kugel in einem Punkt berührt, nennt man Tangentialebene | ||
| − | == | + | ===Bewertung=== |
| + | 1 von 2 Punkten--[[Benutzer:*m.g.*|*m.g.*]] 18:10, 4. Feb. 2013 (CET)<br /> | ||
| + | Tangentialebene sein ist eine zweistellige Relation, es macht erst Sinn, wenn man formuliert ''Tangentialebene der ...'' | ||
| + | |||
| + | ==Lösung User Aaliyah== | ||
| + | |||
| + | Es sei k eine Kugel. Eine Ebene E, die mit der Kugel k genau einen Berührpunkt B hat, nennt man Tangentialebene an der Kugel k.--[[Benutzer:Aaliyah|Aaliyah]] 19:00, 4. Feb. 2013 (CET) | ||
Aktuelle Version vom 10. Februar 2013, 00:16 Uhr
|
Aufgabe aEs seien Lösung User Ron{P/ Zw (A,P,B)} U {A,B} Bewertung2 von 2 Punkten Lösung User ...Aufgabe bDefinieren Sie den Begriff komplanar für die Anzahl von Punkten, ab der der Begriff sinnvoll ist. Lösung User ...Eine Menge von Punkten heißt komplanar, wenn es eine Ebene gibt, die alle Punkte der Menge enthält. Bewertung1 von 2 Punkten --*m.g.* 18:01, 4. Feb. 2013 (CET) Vier Punkte heißen komplanar, wenn sie in ein und derselben Ebene liegen.--Caro44 20:01, 4. Feb. 2013 (CET) Vier Punkte A, B, C, und D sind komplanar, wenn es eine Ebene gibt, die alle diese Punkte enthält. --...lw)... 10:45, 5. Feb. 2013 (CET) Lösung User ...
Bemerkung --*m.g.* 23:18, 9. Feb. 2013 (CET)Gerade wegen Axiom I/4, welches ja aussagt, dass drei Punkte immer komplanar sind, macht die Definition erst ab 4 Punkten so richtig Sinn. Analogie: Sehnendreieck, Sehnenviereck. Aufgabe cDefinieren Sie den Begriff Raute unter Verwendung des Oberbegriffs Viereck. Lösung User RonEin Viereck ist eine Raute, wenn alle vier Seiten gleich lang sind. Bewertung2 von 2 Punkten--*m.g.* 18:02, 4. Feb. 2013 (CET) Lösung ...lw)...Eine Raute ist ein Viereck mit zwei Paar paralleler und 3 gleichlangen Seiten. --...lw)... 10:46, 5. Feb. 2013 (CET) Lösung User RonWenn ein Viereck eine Raute ist, dann sind alle vier Seiten des Vierecks gleich lang. Bewertung0 von 2 Punkten--*m.g.* 18:03, 4. Feb. 2013 (CET) Aufgabe dNur unter Verwendung der Eigenschaft
Lösung User RonEin Kriterium Bewertung2 von 2 Punkten
Lösung User --Sweetnightmare5 19:27, 5. Feb. 2013 (CET)Hinreichende Bedingung --Dothewave 22:06, 9. Feb. 2013 (CET)-- Dothewave Also ich glaube auch, dass es eine hinreichende Bedingung ist. Begründung: Die Eigenschaft E1 ist nicht zwingend erforderlich, um den Begriff B zu definieren. Es könnte auch eine andere Eigenschaft verwednet werden. Ein Kriterium sagt aus, dass GENAU DANN wenn die Eigenschaft auftriff die Bedingung erfüllt ist. Dort ist sie hinreichent und auch notwenig zugleich und daher nicht austauschbar. Also soweit mein Verständnig, wenn jemand mehr weiß,wäre auch ich dankbar um die richtige Antwort. Bemerkungen--*m.g.* 00:16, 10. Feb. 2013 (CET)Meine Bewertung: 1 von 2 Punkten Warum nicht die volle Punktzahl? Es ist sicherlich richtig, dass Definierende Eigenschaften müssen immer notwendig und hinreichend und somit Kriterien sein.
Offenbar nicht, denn wir haben nur Rauten aussortiert. Diese sind Parallelogramme, jedoch sehr spezifische. Ein Großteil der Parallelogramme ist uns entwischt. Oh, vielleicht ist es ja gar nicht notwendig so viel zu messen. Vielleicht reicht es ja aus, nur ein Paar gegenüberliegender Seiten zu messen. Das halbiert unseren Aufwand. Frisch machen wir uns wieder ans Werk. Auf unserem aussortierten Haufen liegen jetzt wieder alle Rauten und nicht nur die alle beliebigen Parallelogramme auch. Auch der Spezialfall Rechteck ist dabei. Zu unserem Entsetzen stellen wir jetzt jedoch fest, dass unser Verfahren nicht trennscharf genug ist. Neben allen Parallelogrammen haben wir quasi als Beifang auch die gleichschenkligen Trapeze dabei, die keine Parallelogramme sind. Ziemlich unökologisch das Ganze. Neben den Thunfischen (die man eigentlich auch nicht mehr fangen sollte) haben wir auch Delfine im Netz. Es ist zwar notwendig, für ein Viereck ein Paar gegenüberliegender zu einander kongruente Seiten zu haben, um zum Parallelogramm zu avancieren, hinreichend (ausreichend) ist diese Eigenschaft jedoch nicht. Um den Begriff sauber zu definieren brauchen wir also eine Bedingung, die sowohl hinreichend als auch notwenig ist. Anders ausgedrückt: Wir brauchen ein Kriterium.
Wir melden unsere Methode zum Patent an und lassen offiziell verkünden, dass Alle Vierecke mit zwei Paaren einander gegenüberliegender Seiten, die jeweils kongruent zueinander sind, ab heute Parallelogramme heißen. Schön und gut, es dauert nicht lange bis uns eine Mitteilung aus der Parallelwelt erreicht: bei uns sind die und nur die Vierecke Parallelogramme, die zwei Paare zueinander paralleler Seiten haben. Vor einigen Jahren hätte uns diese Mitteilung kalt gelassen. Es ist nun jedoch politischer Wille von ganz oben und in Brüssel, die Parallelwelt in Europa aufzunehmen. Die politischen Vertreter der Parallelwelt haben bereits offiziell erklärt, dass Sie auf keinen Fall davon abrücken werden, unter Parallelogrammen Vierecke mit zwei Paaren zueinander paralleler Seiten zu verstehen. Das ist eine nationale Besonderheit und schon weil das Parallelogramm seit Urzeiten das Staatswappen der Parallelwelt ist, wir man diesbezüglich keine Kompromisse eingehen. Die EU könne ja auch ihre Definition der der Parallelwelt anpassen. Also die Bildzeitung eines Tages nicht recht weiß, was zu berichten wäre(Frau Elvers-Elbertzhagen trinkt wieder, aber das interessiert schon lange keine Sau mehr) bringt sie die Schlagzeile: Parallelwelt erpresst EU mit Parallelogrammdefinition, wieviel Parallelogramm dürfen wir noch sein? Verhindern Sie rechtsradikale Aufmärsche und schreiben Sie die Story zu einem guten Ende weiter ... --*m.g.* 00:16, 10. Feb. 2013 (CET) Aufgabe aEs seien Lösung User Ron{P/ Zw (A,P,B)} U {A,B} Bewertung2 von 2 Punkten Lösung User ...Aufgabe bDefinieren Sie den Begriff komplanar für die Anzahl von Punkten, ab der der Begriff sinnvoll ist. Lösung User ...Eine Menge von Punkten heißt komplanar, wenn es eine Ebene gibt, die alle Punkte der Menge enthält. Bewertung1 von 2 Punkten --*m.g.* 18:01, 4. Feb. 2013 (CET) Vier Punkte heißen komplanar, wenn sie in ein und derselben Ebene liegen.--Caro44 20:01, 4. Feb. 2013 (CET) Vier Punkte A, B, C, und D sind komplanar, wenn es eine Ebene gibt, die alle diese Punkte enthält. --...lw)... 10:45, 5. Feb. 2013 (CET) Lösung User ...
Bemerkung --*m.g.* 23:18, 9. Feb. 2013 (CET)Gerade wegen Axiom I/4, welches ja aussagt, dass drei Punkte immer komplanar sind, macht die Definition erst ab 4 Punkten so richtig Sinn. Analogie: Sehnendreieck, Sehnenviereck. Aufgabe cDefinieren Sie den Begriff Raute unter Verwendung des Oberbegriffs Viereck. Lösung User RonEin Viereck ist eine Raute, wenn alle vier Seiten gleich lang sind. Bewertung2 von 2 Punkten--*m.g.* 18:02, 4. Feb. 2013 (CET) Lösung ...lw)...Eine Raute ist ein Viereck mit zwei Paar paralleler und 3 gleichlangen Seiten. --...lw)... 10:46, 5. Feb. 2013 (CET) Lösung User RonWenn ein Viereck eine Raute ist, dann sind alle vier Seiten des Vierecks gleich lang. Bewertung0 von 2 Punkten--*m.g.* 18:03, 4. Feb. 2013 (CET) Aufgabe dNur unter Verwendung der Eigenschaft
Lösung User RonEin Kriterium Bewertung2 von 2 Punkten
Lösung User --Sweetnightmare5 19:27, 5. Feb. 2013 (CET)Hinreichende Bedingung --Dothewave 22:06, 9. Feb. 2013 (CET)-- Dothewave Also ich glaube auch, dass es eine hinreichende Bedingung ist. Begründung: Die Eigenschaft E1 ist nicht zwingend erforderlich, um den Begriff B zu definieren. Es könnte auch eine andere Eigenschaft verwednet werden. Ein Kriterium sagt aus, dass GENAU DANN wenn die Eigenschaft auftriff die Bedingung erfüllt ist. Dort ist sie hinreichent und auch notwenig zugleich und daher nicht austauschbar. Also soweit mein Verständnig, wenn jemand mehr weiß,wäre auch ich dankbar um die richtige Antwort.
BewertungMeine Bewertung: 1 von 2 Punkten Definierende Eigenschaften müssen immer notwendig und hinreichend und somit Kriterien sein.
Offenbar nicht, denn wir haben nur Rauten aussortiert. Diese sind Parallelogramme, jedoch sehr spezifische. Ein Großteil der Parallelogramme ist uns entwischt. Oh, vielleicht ist es ja gar nicht notwendig so viel zu messen. Vielleicht reicht es ja aus, nur ein Paar gegenüberliegender Seiten zu messen. Das halbiert unseren Aufwand. Frisch machen wir uns wieder ans Werk. Auf unserem aussortierten Haufen liegen jetzt wieder alle Rauten und nicht nur die alle beliebigen Parallelogramme auch. Auch der Spezialfall Rechteck ist dabei. Zu unserem Entsetzen stellen wir jetzt jedoch fest, dass unser Verfahren nicht trennscharf genug ist. Neben allen Parallelogrammen haben wir quasi als Beifang auch die gleichschenkligen Trapeze dabei, die keine Parallelogramme sind. Ziemlich unökologisch das Ganze. Neben den Thunfischen (die man eigentlich auch nicht mehr fangen sollte) haben wir auch Delfine im Netz. Es ist zwar notwendig, für ein Viereck ein Paar gegenüberliegender zu einander kongruente Seiten zu haben, um zum Parallelogramm zu avancieren, hinreichend (ausreichend) ist diese Eigenschaft jedoch nicht. Um den Begriff sauber zu definieren brauchen wir also eine Bedingung, die sowohl hinreichend als auch notwenig ist. Anders ausgedrückt: Wir brauchen ein Kriterium.
Wir melden unsere Methode zum Patent an und lassen offiziell verkünden, dass Alle Vierecke mit zwei Paaren einander gegenüberliegender Seiten, die jeweils kongruent zueinander sind, ab heute Parallelogramme heißen. Schön und gut, es dauert nicht lange bis uns eine Mitteilung aus der Parallelwelt erreicht: bei uns sind die und nur die Vierecke Parallelogramme, die zwei Paare zueinander paralleler Seiten haben. Vor einigen Jahren hätte uns diese Mitteilung kalt gelassen. Es ist nun jedoch politischer Wille von ganz oben und in Brüssel, die Parallelwelt in Europa aufzunehmen. Die politischen Vertreter der Parallelwelt haben bereits offiziell erklärt, dass Sie auf keinen Fall davon abrücken werden, unter Parallelogrammen Vierecke mit zwei Paaren zueinander paralleler Seiten zu verstehen. Das ist eine nationale Besonderheit und schon weil das Parallelogramm seit Urzeiten das Staatswappen der Parallelwelt ist, wir man diesbezüglich keine Kompromisse eingehen. Die EU könne ja auch ihre Definition der der Parallelwelt anpassen. Also die Bildzeitung eines Tages nicht recht weiß, was zu berichten wäre(Frau Elvers-Elbertzhagen trinkt wieder, aber das interessiert schon lange keine Sau mehr) bringt sie die Schlagzeile: Parallelwelt erpresst EU mit Parallelogrammdefinition, wieviel Parallelogramm dürfen wir noch sein? Verhindern Sie rechtsradikale Aufmärsche und schreiben Sie die Story zu einem guten Ende weiter ... --*m.g.* 00:14, 10. Feb. 2013 (CET) Lösung User ...Aufgabe eEs sei Lösung User ...Eine Kugel Bewertung1 von 2 Punkten--*m.g.* 18:04, 4. Feb. 2013 (CET) Lösung User AaliyahEs ist eine Kugel um P mit dem Radius r inklusive ihres Inneren.--Aaliyah 18:55, 4. Feb. 2013 (CET)
Lösung User ...lw)...M ist eine Kugel mit dem Radius RP. --...lw)... 10:50, 5. Feb. 2013 (CET) Aufgabe fDefinieren Sie den Begriff Rechter Winkel wie in der Vorlesung.
Lösung User RonEin Winkel, der so groß ist, wie einer seiner Nebenwinkel, nennt man rechter Winkel. Bewertung2 von 2 Punkten mit sehr großen Bauchschmerzen: Lösung User AaliyahWenn ein Winkel so groß ist, wie einer seiner Nebenwinkel, dann ist der Winkel ein Rechter.--Aaliyah 18:57, 4. Feb. 2013 (CET) Aufgabe gErgänzen Sie die folgende Definition: Zwei Geraden
Lösung User Ron,wenn sie nicht parallel sind und keinen gemeinsamen Schnittpunkt(schnittfrei sind) haben Bewertung2 von 2 Punkten, besser schnittpunktfrei --*m.g.* 18:08, 4. Feb. 2013 (CET) Lösung User ...Aufgabe hDefinieren Sie den Begriff Tangentialebene einer Kugel.
Lösung User RonEine Ebene, welche eine Kugel in einem Punkt berührt, nennt man Tangentialebene Bewertung1 von 2 Punkten--*m.g.* 18:10, 4. Feb. 2013 (CET) Lösung User AaliyahEs sei k eine Kugel. Eine Ebene E, die mit der Kugel k genau einen Berührpunkt B hat, nennt man Tangentialebene an der Kugel k.--Aaliyah 19:00, 4. Feb. 2013 (CET)
|
Lösung User ...
Aufgabe e
Es sei  ein beliebiger Punkt und
ein beliebiger Punkt und 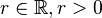 . Was ist das?
. Was ist das? 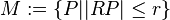 .
.
Die Punktmenge M ist das Volumen einer Kugel mit Mittelpunkt R und Radius r.--Natürliches Mineralwasser 20:50, 9. Feb. 2013 (CET)
Lösung User ...
Eine Kugel
Bewertung
1 von 2 Punkten--*m.g.* 18:04, 4. Feb. 2013 (CET)
Lösung User Aaliyah
Es ist eine Kugel um P mit dem Radius r inklusive ihres Inneren.--Aaliyah 18:55, 4. Feb. 2013 (CET)
Lösung User ...lw)...
M ist eine Kugel mit dem Radius RP. --...lw)... 10:50, 5. Feb. 2013 (CET)
Aufgabe f
Definieren Sie den Begriff Rechter Winkel wie in der Vorlesung.
Lösung User Ron
Ein Winkel, der so groß ist, wie einer seiner Nebenwinkel, nennt man rechter Winkel.
Bewertung
2 von 2 Punkten mit sehr großen Bauchschmerzen:
Wen oder was nennt man rechter Winkel? Einen Winkel, der ...--*m.g.* 18:06, 4. Feb. 2013 (CET)
Lösung User Aaliyah
Wenn ein Winkel so groß ist, wie einer seiner Nebenwinkel, dann ist der Winkel ein Rechter.--Aaliyah 18:57, 4. Feb. 2013 (CET)
Aufgabe g
Ergänzen Sie die folgende Definition: Zwei Geraden  und
und  sind windschief, wenn
sind windschief, wenn 
Lösung User Ron
,wenn sie nicht parallel sind und keinen gemeinsamen Schnittpunkt(schnittfrei sind) haben
Bewertung
2 von 2 Punkten, besser schnittpunktfrei --*m.g.* 18:08, 4. Feb. 2013 (CET)
Lösung User ...
Aufgabe h
Definieren Sie den Begriff Tangentialebene einer Kugel.
Lösung User Ron
Eine Ebene, welche eine Kugel in einem Punkt berührt, nennt man Tangentialebene
Bewertung
1 von 2 Punkten--*m.g.* 18:10, 4. Feb. 2013 (CET)
Tangentialebene sein ist eine zweistellige Relation, es macht erst Sinn, wenn man formuliert Tangentialebene der ...
Lösung User Aaliyah
Es sei k eine Kugel. Eine Ebene E, die mit der Kugel k genau einen Berührpunkt B hat, nennt man Tangentialebene an der Kugel k.--Aaliyah 19:00, 4. Feb. 2013 (CET)
|}
</div>
 und
und  zwei verschiedene Punkte.
zwei verschiedene Punkte.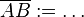 .
.
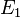 sei der Begriff
sei der Begriff 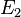 hätte definiert werden können.
hätte definiert werden können.
