Lösung von Aufgabe 4.1 P (SoSe 13): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(Die Seite wurde neu angelegt: „Beweisen Sie mit Hilfe einer Wahrheitstabelle:<br /><br /> <math>(\ A \Rightarrow B) \ \Leftrightarrow (\neg B \Rightarrow \neg A)</math><br /> Inwiefern hilf…“) |
|||
| (3 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 2: | Zeile 2: | ||
<math>(\ A \Rightarrow B) \ \Leftrightarrow (\neg B \Rightarrow \neg A)</math><br /> | <math>(\ A \Rightarrow B) \ \Leftrightarrow (\neg B \Rightarrow \neg A)</math><br /> | ||
| − | |||
| + | {| class="wikitable " | ||
| + | |- style="background: #DDFFDD;" | ||
| + | ! A | ||
| + | ! B | ||
| + | ! A ⇒ B | ||
| + | ! ¬B | ||
| + | ! ¬A | ||
| + | ! ¬B ⇒ ¬A | ||
| + | |- | ||
| + | | W | ||
| + | | W | ||
| + | | W | ||
| + | | F | ||
| + | | F | ||
| + | | W | ||
| + | |- | ||
| + | | W | ||
| + | | F | ||
| + | | F | ||
| + | | W | ||
| + | | F | ||
| + | | F | ||
| + | |- | ||
| + | | F | ||
| + | | W | ||
| + | | W | ||
| + | | F | ||
| + | | W | ||
| + | | W | ||
| + | |- | ||
| + | | F | ||
| + | | F | ||
| + | | W | ||
| + | | W | ||
| + | | W | ||
| + | | W | ||
| + | |}<br /> | ||
| + | --[[Benutzer:Nolessonlearned|Nolessonlearned]] 12:35, 14. Mai 2013 (CEST)<br /> | ||
| + | |||
| + | Inwiefern hilft Ihnen diese Äquivalenz, wenn Sie einen geometrischen Satz beweisen wollen?<br /> | ||
| + | *Diese Äquivalenz legitimiert die Verwendung der indirekten Beweisform Kontraposition.--[[Benutzer:Nolessonlearned|Nolessonlearned]] 12:40, 14. Mai 2013 (CEST)<br /> | ||
| + | So ist es!--[[Benutzer:Tutorin Anne|Tutorin Anne]] 10:01, 23. Mai 2013 (CEST) | ||
[[Category:Einführung_P]] | [[Category:Einführung_P]] | ||
Aktuelle Version vom 23. Mai 2013, 09:01 Uhr
Beweisen Sie mit Hilfe einer Wahrheitstabelle:
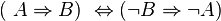
| A | B | A ⇒ B | ¬B | ¬A | ¬B ⇒ ¬A |
|---|---|---|---|---|---|
| W | W | W | F | F | W |
| W | F | F | W | F | F |
| F | W | W | F | W | W |
| F | F | W | W | W | W |
--Nolessonlearned 12:35, 14. Mai 2013 (CEST)
Inwiefern hilft Ihnen diese Äquivalenz, wenn Sie einen geometrischen Satz beweisen wollen?
- Diese Äquivalenz legitimiert die Verwendung der indirekten Beweisform Kontraposition.--Nolessonlearned 12:40, 14. Mai 2013 (CEST)
So ist es!--Tutorin Anne 10:01, 23. Mai 2013 (CEST)

