Lösung von Aufgabe 4.05 S SoSe 13: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „<div style="margin:0; margin-right:4px; border:1px solid #27408B; padding: 1em 1em 1em 1em; background-color:#FFFF99; align:left;"> {|width=80%| style="background…“) |
*m.g.* (Diskussion | Beiträge) |
||
| Zeile 3: | Zeile 3: | ||
| valign="top" | | | valign="top" | | ||
<!--- ---------------------------------------------------------------- ---> | <!--- ---------------------------------------------------------------- ---> | ||
| − | + | ==Aufgabe 4.05== | |
| + | Wir gehen davon aus, dass wir der ebenen Geometrie ein kartesisches Koordinatensystem zugrunde gelegt haben. Bezüglich dieses Systems definieren wir die folgenden beiden Punktmengen: | ||
| + | #<math>A:=\left\{P\left(x_P,y_P\right)|y_p=\frac{3}{4}x_p - \frac{7}{8}\right\}</math> | ||
| + | #<math>B:=\left\{P\left(x_P,y_P\right)|y_p=\frac{36,3}{48,4}x_p - 0,875\right\}</math> | ||
| + | Beweisen Sie <math>A \cap B = A</math>.<br /> | ||
==Lösung User ...== | ==Lösung User ...== | ||
Aktuelle Version vom 13. Mai 2013, 13:52 Uhr
Aufgabe 4.05Wir gehen davon aus, dass wir der ebenen Geometrie ein kartesisches Koordinatensystem zugrunde gelegt haben. Bezüglich dieses Systems definieren wir die folgenden beiden Punktmengen: Beweisen Sie Lösung User ...Lösung User ...Lösung User ...
|
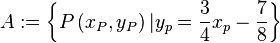
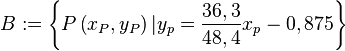
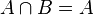 .
.
