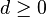Lösung von Aufgabe 4.07 S SoSe 13: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) |
*m.g.* (Diskussion | Beiträge) (→Lösung User ...) |
||
| (Eine dazwischenliegende Version von einem Benutzer wird nicht angezeigt) | |||
| Zeile 9: | Zeile 9: | ||
==Lösung User ...== | ==Lösung User ...== | ||
| + | |||
| + | * Zwei Gerade sind parallel, wenn sie sich nicht schneiden und nicht windschief zueinernader sind. | ||
| + | * Zu jedem Punkt der Gerade g1 kann man ein Lot auf die Gerade g2 fällen. Der Betrag d der Länge des Lots ist dabei immer gleichbleibend. <br /> | ||
| + | <math>d \ge 0</math> | ||
| + | |||
| + | ===Bemerkung--[[Benutzer:*m.g.*|*m.g.*]] 23:18, 3. Jun. 2013 (CEST)=== | ||
| + | Bei der ersten Definition müsste klar sein, was windschief bedeutet. Geraden sollen auch dann parallel sein, wenn sie identisch sind. (Jede Gerade ist zu sich selbst parallel.) Diesen Fall haben Sie nicht berücksichtigt.<br /><br /> | ||
| + | |||
| + | |||
| + | |||
| + | In der zweiten Definition erkennen ich was gemeint ist. Sie ist so jedoch nicht korrekt. Einfacher: Wenn zwei geraden in allen Punkten denselben Abstand zueinander haben, dann sind sie parallel. (inklusive Abstand 0) | ||
==Lösung User ...== | ==Lösung User ...== | ||
Aktuelle Version vom 3. Juni 2013, 22:18 Uhr
Aufgabe 4.07Definieren Sie den Begriff der Parallelität für Geraden.
(Hinweis: Der Mathematiker hat sehr großes Interesse daran, dass die Relation parallel auf der Menge aller Geraden reflexiv ist, d.h. dass jede Gerade zu sich selbst parallel ist.) Lösung User ...
Bemerkung--*m.g.* 23:18, 3. Jun. 2013 (CEST)Bei der ersten Definition müsste klar sein, was windschief bedeutet. Geraden sollen auch dann parallel sein, wenn sie identisch sind. (Jede Gerade ist zu sich selbst parallel.) Diesen Fall haben Sie nicht berücksichtigt.
In der zweiten Definition erkennen ich was gemeint ist. Sie ist so jedoch nicht korrekt. Einfacher: Wenn zwei geraden in allen Punkten denselben Abstand zueinander haben, dann sind sie parallel. (inklusive Abstand 0) Lösung User ...Lösung User ...
|