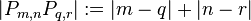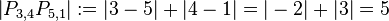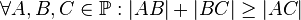Lösung von Aufgabe 6.09 S SoSe 13: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „<div style="margin:0; margin-right:4px; border:1px solid #27408B; padding: 1em 1em 1em 1em; background-color:#FFFF99; align:left;"> {|width=80%| style="background…“) |
*m.g.* (Diskussion | Beiträge) |
||
| (Eine dazwischenliegende Version von einem Benutzer wird nicht angezeigt) | |||
| Zeile 4: | Zeile 4: | ||
<!--- ---------------------------------------------------------------- ---> | <!--- ---------------------------------------------------------------- ---> | ||
| − | + | ==Aufgabe 6.09== | |
| + | Wir betrachten die folgende Menge <math>\mathbb{P}</math>von Modellpunkten:<br /> | ||
| + | <math>\mathbb{P}:=\{P_{i,j}|0 \leq i \leq 9 \wedge 0 \leq j \leq 9 \}</math>.<br /> | ||
| + | Auf der Menge der Modellpunkte definieren wir den Abstand zweier Modellpunkte <math>P_{m,n}</math> und <math>P_{q,r}</math>:<br /> | ||
| + | <math>\left|P_{m,n}P_{q,r}\right|:=|m-q|+|n-r|</math><br /><br /> | ||
| + | Beispiel:<br /> | ||
| + | <math>\left|P_{3,4}P_{5,1}\right|:=|3-5|+|4-1|=|-2|+|3|=5</math> | ||
| + | <br /> Untersuchen Sie, ob in dem Modell die Dreiecksungleichung erfüllt ist:<br /> | ||
| + | <math>\forall A,B,C \in \mathbb{P}: |AB|+|BC|\geq |AC|</math><br /><br /> | ||
==Lösung User ...== | ==Lösung User ...== | ||
Aktuelle Version vom 4. Juni 2013, 08:24 Uhr
Aufgabe 6.09Wir betrachten die folgende Menge Lösung User ...Lösung User ...Lösung User ...
|
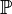von Modellpunkten:
.
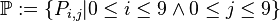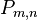und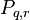 
:
