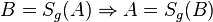Die Geradenspiegelung und ihre Eigenschaften SoSe 13: Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: „Im Folgenden werden wir uns mit Geometrie in der Ebene beschäftigen. Speziell betrachten wir so genannte Abbildungen der Ebene auf sich selbst und hier wiederum …“) |
(→Eigenschaften einer Geradenspiegelung) |
||
| (4 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 22: | Zeile 22: | ||
::formal: <math>P=\varphi (P)=P'</math><br /><br /> | ::formal: <math>P=\varphi (P)=P'</math><br /><br /> | ||
Aufgabe: Welche Punkte sind bei der Geradenspiegelung Fixpunkte?<br /><br /> | Aufgabe: Welche Punkte sind bei der Geradenspiegelung Fixpunkte?<br /><br /> | ||
| + | * Alle Punkte der Geraden P sind Fixpunkte | ||
==== Definition V.5 : (Fixgerade)==== | ==== Definition V.5 : (Fixgerade)==== | ||
::Wenn bei einer Abbildung <math>\varphi</math> eine Bildgerade ''g''' mit ihrem Urbild ''g'' zusammenfällt, dann heißt ''g'' Fixgerade der Abbildung <math>\varphi</math>.<br /><br /> | ::Wenn bei einer Abbildung <math>\varphi</math> eine Bildgerade ''g''' mit ihrem Urbild ''g'' zusammenfällt, dann heißt ''g'' Fixgerade der Abbildung <math>\varphi</math>.<br /><br /> | ||
Aufgabe: Gibt es Fixgeraden bei der Geradenspiegelung und welche sind dies ggf.?<br /><br /> | Aufgabe: Gibt es Fixgeraden bei der Geradenspiegelung und welche sind dies ggf.?<br /><br /> | ||
| + | * Die Fixgeraden sind senkrecht auf g bzw. parallel zur Gerade von P | ||
==== Definition V.6 : (Fixpunktgerade)==== | ==== Definition V.6 : (Fixpunktgerade)==== | ||
::Wenn jeder Punkt ''P'' einer Fixgeraden ''g'' auf sich selbst abgebildet wird, so ist die Fixgerade ''g'' auch Fixpunktgerade.<br /><br /> | ::Wenn jeder Punkt ''P'' einer Fixgeraden ''g'' auf sich selbst abgebildet wird, so ist die Fixgerade ''g'' auch Fixpunktgerade.<br /><br /> | ||
Aufgabe: Gibt es Fixpunktgeraden bei der Geradenspiegelung und welche sind dies ggf.?<br /><br /> | Aufgabe: Gibt es Fixpunktgeraden bei der Geradenspiegelung und welche sind dies ggf.?<br /><br /> | ||
| + | * Die Fixpunktgerade ist in diesem Fall die Spiegelachse | ||
===Eigenschaften einer Geradenspiegelung=== | ===Eigenschaften einer Geradenspiegelung=== | ||
| − | *abstandserhaltend: Der Abstand <math>\left| A'B' \right|</math> zweier Bildpunkte | + | *abstandserhaltend: Der Abstand <math>\left| A'B' \right|</math> zweier Bildpunkte <math>A'</math> und <math>B'</math> ist gleich dem Abstand <math>\left| AB \right|</math> der beiden Urbilder ''A'' und ''B''. |
*winkelmaßerhaltend: hier gilt analog: <math>\left| \angle ABC \right|= \left| \angle A'B'C' \right|</math><br /><br /> | *winkelmaßerhaltend: hier gilt analog: <math>\left| \angle ABC \right|= \left| \angle A'B'C' \right|</math><br /><br /> | ||
diese beiden Eigenschaften lassen sich axiomatisch begründen, was wir hier aber nicht weiter vertiefen wollen. Alle weiteren Eigenschaften lassen sich aus der Abstands- und Winkelmaßerhaltung ableiten.<br /><br /> | diese beiden Eigenschaften lassen sich axiomatisch begründen, was wir hier aber nicht weiter vertiefen wollen. Alle weiteren Eigenschaften lassen sich aus der Abstands- und Winkelmaßerhaltung ableiten.<br /><br /> | ||
| Zeile 66: | Zeile 69: | ||
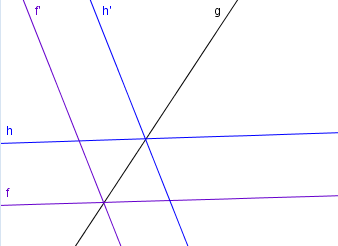
==== Satz V.7 (Parallelentreue der Geradenspiegelung <math>S_g </math>): ==== | ==== Satz V.7 (Parallelentreue der Geradenspiegelung <math>S_g </math>): ==== | ||
| − | Bei der Geradenspiegelung <math>S_g </math> werden zueinander parallele Geraden | + | Bei der Geradenspiegelung <math>S_g </math> werden zueinander parallele Geraden <math>f</math> und <math> h</math> auf zwei zueinander parallele Geraden <math>f'</math> und <math>h'</math> abgebildet.<br /> |
| − | Beweis: | + | |
| + | [[Datei: Parallelentreue_Geradenspiegelung.PNG]] | ||
| + | |||
| + | |||
| + | |||
| + | Beweis: siehe Zusatzaufgabe Übung 9<br /> | ||
Aktuelle Version vom 26. Juni 2013, 17:20 Uhr
Im Folgenden werden wir uns mit Geometrie in der Ebene beschäftigen. Speziell betrachten wir so genannte Abbildungen der Ebene auf sich selbst und hier wiederum nur ganz bestimmte Abbildungen, die so genannten Kongruenzabbildungen.
Definition V.1 : (Abbildung  )
)
- Eine Zuordnung, die jedem Punkt P der Ebene eindeutig einen Bildpunkt P' zuordnet, nennt man Abbildung.
- Schreibweise: Fehler beim Parsen(Lexikalischer Fehler): P'=\varphi\(P)
- Eine Zuordnung, die jedem Punkt P der Ebene eindeutig einen Bildpunkt P' zuordnet, nennt man Abbildung.
Definition V.2 : (involutorische Abbildung)
- Eine Abbildung
 , die bei zweifacher Ausführung (
, die bei zweifacher Ausführung (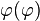 ) wieder zum Ursprungsbild führt (identische Abbildung), nennt man involutorisch oder involutorische Abbildung.
) wieder zum Ursprungsbild führt (identische Abbildung), nennt man involutorisch oder involutorische Abbildung.
- Eine Abbildung
Definition V.3 : (Geraden- oder Achsenspiegelung 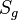 )
)
- Gegeben sei eine Gerade g in der Ebene. Die Geraden- oder Achsenspiegelung
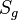 ist die Abbildung der Ebene auf sich selbst, die nach folgender Abbildungsvorschrift jeden Punkt P seinem Bildpunkt P' zuordnet.
ist die Abbildung der Ebene auf sich selbst, die nach folgender Abbildungsvorschrift jeden Punkt P seinem Bildpunkt P' zuordnet.
- Gegeben sei eine Gerade g in der Ebene. Die Geraden- oder Achsenspiegelung
-
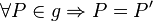
-
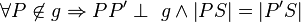 mit
mit 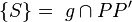
Nutzen Sie die folgende GeoGebra-Applikation um den Punkt P an der Geraden g zu spiegeln. Verschieben den Punkt P bzw. die Gerade g um die Definition der Geradenspiegelung nachzuvollziehen.
Konstruktion der Geradenspiegelung mit Zirkel und Lineal
Erinnern Sie sich an Ihre Schulzeit zurück: Wie haben Sie in der Schule mit Zirkel und Lineal eine Geradenspiegelung angefertigt?
Ihre Beschreibung (gerne auch als Bild):
Definition V.4 : (Fixpunkte)
- Wenn bei einer Abbildung
 ein Bildpunkt P' mit seinem Urbild P zusammenfällt (P wird auf sich selbst abgebildet), dann heißt P Fixpunkt der Abbildung
ein Bildpunkt P' mit seinem Urbild P zusammenfällt (P wird auf sich selbst abgebildet), dann heißt P Fixpunkt der Abbildung  .
.
- formal:
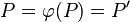
- Wenn bei einer Abbildung
Aufgabe: Welche Punkte sind bei der Geradenspiegelung Fixpunkte?
- Alle Punkte der Geraden P sind Fixpunkte
Definition V.5 : (Fixgerade)
- Wenn bei einer Abbildung
 eine Bildgerade g' mit ihrem Urbild g zusammenfällt, dann heißt g Fixgerade der Abbildung
eine Bildgerade g' mit ihrem Urbild g zusammenfällt, dann heißt g Fixgerade der Abbildung  .
.
- Wenn bei einer Abbildung
Aufgabe: Gibt es Fixgeraden bei der Geradenspiegelung und welche sind dies ggf.?
- Die Fixgeraden sind senkrecht auf g bzw. parallel zur Gerade von P
Definition V.6 : (Fixpunktgerade)
- Wenn jeder Punkt P einer Fixgeraden g auf sich selbst abgebildet wird, so ist die Fixgerade g auch Fixpunktgerade.
- Wenn jeder Punkt P einer Fixgeraden g auf sich selbst abgebildet wird, so ist die Fixgerade g auch Fixpunktgerade.
Aufgabe: Gibt es Fixpunktgeraden bei der Geradenspiegelung und welche sind dies ggf.?
- Die Fixpunktgerade ist in diesem Fall die Spiegelachse
Eigenschaften einer Geradenspiegelung
- abstandserhaltend: Der Abstand
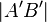 zweier Bildpunkte
zweier Bildpunkte 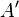 und
und 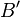 ist gleich dem Abstand
ist gleich dem Abstand  der beiden Urbilder A und B.
der beiden Urbilder A und B.
- winkelmaßerhaltend: hier gilt analog:
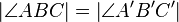
diese beiden Eigenschaften lassen sich axiomatisch begründen, was wir hier aber nicht weiter vertiefen wollen. Alle weiteren Eigenschaften lassen sich aus der Abstands- und Winkelmaßerhaltung ableiten.
Satz V.1 :
Die Geradenspiegelung 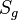 ist eine involutorische Abbildung, d. h. für alle Punkte A, B der Ebene gilt:
ist eine involutorische Abbildung, d. h. für alle Punkte A, B der Ebene gilt:
Beweis:
Satz V.2 (Streckentreue der Geradenspiegelung 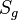 ):
):
Bei der Geradenspiegelung 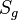 wird eine Strecke
wird eine Strecke  auf eine Strecke
auf eine Strecke 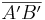 abgebildet. Dabei gilt:
abgebildet. Dabei gilt: 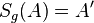 und
und 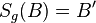 .
.
Beweis:
Satz V.3 (Längentreue der Geradenspiegelung 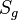 ):
):
Die Länge der Strecke 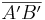 , die bei der Geradenspiegelung
, die bei der Geradenspiegelung 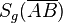 entsteht ist gleich der Länge der Strecke
entsteht ist gleich der Länge der Strecke  .
.
Beweis:
Satz V.4 (Halbgeradentreue der Geradenspiegelung 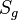 ):
):
Bei der Geradenspiegelung 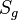 wird eine Halbgerade
wird eine Halbgerade  auf eine Halbgerade
auf eine Halbgerade 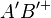 abgebildet. Dabei gilt:
abgebildet. Dabei gilt: 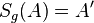 und
und 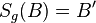 .
.
Beweis:
Satz V.5 (Geradentreue der Geradenspiegelung 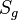 ):
):
Bei der Geradenspiegelung 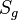 wird eine Gerade
wird eine Gerade  auf eine Gerade
auf eine Gerade 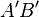 abgebildet. Dabei gilt:
abgebildet. Dabei gilt: 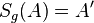 und
und 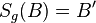 .
.
Beweis:
Satz V.6 (Winkeltreue der Geradenspiegelung 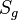 ):
):
Bei der Geradenspiegelung 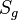 wird ein Winkel
wird ein Winkel  auf einen Winkel
auf einen Winkel 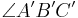 abgebildet. Dabei stimmen die Winkelmaße beider Winkel überein.
abgebildet. Dabei stimmen die Winkelmaße beider Winkel überein.
Beweis:
Satz V.7 (Parallelentreue der Geradenspiegelung 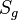 ):
):
Bei der Geradenspiegelung 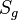 werden zueinander parallele Geraden
werden zueinander parallele Geraden  und
und  auf zwei zueinander parallele Geraden
auf zwei zueinander parallele Geraden 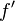 und
und 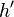 abgebildet.
abgebildet.
Beweis: siehe Zusatzaufgabe Übung 9