Lösung von Aufgabe 9.3P (SoSe 13): Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
 
(14 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt)
Zeile 17: Zeile 17:
 
| 2 <math>Sg(\ BA^{+} )  = \ B'A'^{+}  \wedge  Sg (\ BC^{+} ) = \ B'C'^{+}</math>  || Halbgeradentreue, 1)
 
| 2 <math>Sg(\ BA^{+} )  = \ B'A'^{+}  \wedge  Sg (\ BC^{+} ) = \ B'C'^{+}</math>  || Halbgeradentreue, 1)
 
|-  
 
|-  
−
| 3 <math>\angle A'B'C' = B'A'^{+} n B'C'^{+}</math> || Def Winkel, 2)
+
| 3 <math>\angle A'B'C' = B'A'^{+} \cup B'C'^{+}</math> || Def Winkel, 2)
 
|-  
 
|-  
 
| 4 <math>|\angle ABC| = |\angle A'B'C'|</math> || Winkelmaßerhaltend
 
| 4 <math>|\angle ABC| = |\angle A'B'C'|</math> || Winkelmaßerhaltend
Zeile 23: Zeile 23:
 
| 5 <math>Sg(\angle ABC ) = \angle A'B'C'</math>  || 1)2)4)
 
| 5 <math>Sg(\angle ABC ) = \angle A'B'C'</math>  || 1)2)4)
 
|}
 
|}
−
--[[Benutzer:Regenschirm|Regenschirm]] 18:13, 25. Jun. 2013 (CEST)
+
--[[Benutzer:Regenschirm|Regenschirm]] 18:13, 25. Jun. 2013 (CEST)<br />
 +
 
 +
 
 +
Der Beweis ist korrekt.--[[Benutzer:Tutorin Anne|Tutorin Anne]] 15:16, 26. Jun. 2013 (CEST)
 +
 
 +
 
 
<br />
 
<br />
−
[[Kategorie: Einführung_P]]
+
[[Kategorie: Einführung_P]]<br />
 +
<br />
 +
'''Voraussetzung''':<br />
 +
<math>\angle ABC\ mit\ \ BA^{+}\ \cup\  \ BC^{+}\  </math>  <math>mit\ A,B,C \in\ \epsilon</math><br />
 +
<br />
 +
'''Behauptung''': <math>\angle ABC\  \tilde {=}\ \angle A'B'C'</math><br />
 +
<br />
 +
 
 +
{| class="wikitable "
 +
|- style="background: #DDFFDD;"
 +
!
 +
! Beweisschritt
 +
! Begründung
 +
|-
 +
| 1)
 +
| A' = Sg(A)
 +
| Eigenschaft d. GS
 +
|-
 +
| 2)
 +
| B' = Sg(B)
 +
| Eigenschaft d. GS
 +
|-
 +
| 3)
 +
| C' = Sg(C)
 +
| Eigenschaft d. GS
 +
|-
 +
| 4)
 +
| <math>Sg(BA^{+} ) = \ B'A'^{+}</math> 
 +
| (1); (2); Voraussetzung; Halbgeradentreue d. GS
 +
|-
 +
| 5)
 +
| <math>Sg(BC^{+} ) = \ B'C'^{+}</math> 
 +
| (2); (3); Voraussetzung; Halbgeradentreue d. GS
 +
|-
 +
| 6)
 +
| <math>\left| \angle ABC\  \right|\ =\ \left| \angle A'B'C'\  \right| </math>
 +
| (4); (5); Winkelmaßerhaltung d. GS;
 +
|-
 +
| 7)
 +
| <math>\angle ABC\  \tilde {=} \ \angle A'B'C' </math>
 +
| (4); (5); (6); Winkelkongruenz
 +
q.e.d.
 +
|}--[[Benutzer:Nolessonlearned|Nolessonlearned]] 13:27, 15. Jul. 2013 (CEST)<br />
 +
Der Beweis ist so nicht richtig. Es gibt keine kongruenten Halbgeraden, da wir Kongruenz von Halbgeraden nicht definiert haben (und ich auch nicht wüsste, wie man es definieren sollte). Schritt 1-3 ist lediglich eine Benennung, die aus der Def. Geradenspiegelung folgt. Schreibe Benennungen lieber in die Voraussetzung, v.a. da du diese ja bereits in der Behauptung nutzt. --[[Benutzer:Tutorin Anne|Tutorin Anne]] 13:27, 16. Jul. 2013 (CEST)<br />
 +
* Wir hatten doch mal die Halbgeradentreue bewiesen. Ich ging davon aus, dass bei der Halbgeradentreue die Halbgeraden kongruent zueinander sind.--[[Benutzer:Nolessonlearned|Nolessonlearned]] 21:31, 16. Jul. 2013 (CEST)<br /> Ist nicht so, zumindest wäre mir das total neu.<br />
 +
** Was muss ich mir dann unter der Halbgeradentreue vorstellen?--[[Benutzer:Nolessonlearned|Nolessonlearned]] 12:30, 18. Jul. 2013 (CEST)<br />
 +
Die Halbgeradentreue besagt einfach nur : Sg (AB+) = A'B'+; Halbgeraden werden auf Halbgeraden abgebildet, sie weren nicht zur Kreisen, Wellen, Winkeln, Geraden oder sonst etwas. Das hat nichts mit dem Wort kongruent zu tun. Es gibt auch keine kongrente Geraden. --[[Benutzer:Tutorin Anne|Tutorin Anne]] 21:02, 18. Jul. 2013 (CEST)<br />
 +
***Ist vielleicht eine doofe Frage, aber warum gibt es eine Streckenkongruenz, aber keine Geraden- oder Halbgeradenkongruenz?--[[Benutzer:Nolessonlearned|Nolessonlearned]] 21:53, 18. Jul. 2013 (CEST)<br />
 +
****Gute Frage! Und die Antwort ist einfach :). Stecken und Winkel haben ein Maß. Kongruenz ist definiert über dieses Maß. Da Halbgeraden und Geraden kein Längenmaß, also keine Längenangabe haben, kann ich die Relation Kongruenz nicht brauchen.--[[Benutzer:Tutorin Anne|Tutorin Anne]] 10:56, 19. Jul. 2013 (CEST)

Aktuelle Version vom 19. Juli 2013, 09:56 Uhr

Beweisen Sie die Winkeltreue der Geradenspiegelung. Nutzen Sie für den Beweis die Halbgeradentreue und die Eigenschaft der Geradenspiegelung winkelmaßerhaltend zu sein.


Voraussetzung 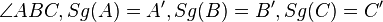\angle ABC, Sg(A)=A', Sg(B)=B', Sg(C)=C'
Behauptung 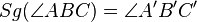Sg(\angle ABC ) = \angle A'B'C'



Beweisschritt Begründung
1 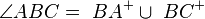\angle ABC = \ BA^{+} \cup \ BC^{+} Voraussetzung, Def. Winkel
2 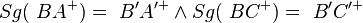Sg(\ BA^{+} ) = \ B'A'^{+} \wedge Sg (\ BC^{+} ) = \ B'C'^{+} Halbgeradentreue, 1)
3 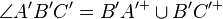\angle A'B'C' = B'A'^{+} \cup B'C'^{+} Def Winkel, 2)
4 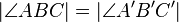|\angle ABC| = |\angle A'B'C'| Winkelmaßerhaltend
5 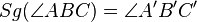Sg(\angle ABC ) = \angle A'B'C' 1)2)4)

--Regenschirm 18:13, 25. Jun. 2013 (CEST)


Der Beweis ist korrekt.--Tutorin Anne 15:16, 26. Jun. 2013 (CEST)





Voraussetzung:
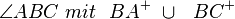
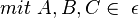
\angle ABC\ mit\ \ BA^{+}\ \cup\ \ BC^{+}\ mit\ A,B,C \in\ \epsilon

Behauptung: 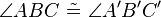\angle ABC\ \tilde {=}\ \angle A'B'C'

Beweisschritt Begründung
1) A' = Sg(A) Eigenschaft d. GS
2) B' = Sg(B) Eigenschaft d. GS
3) C' = Sg(C) Eigenschaft d. GS
4) 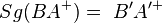Sg(BA^{+} ) = \ B'A'^{+} (1); (2); Voraussetzung; Halbgeradentreue d. GS
5) 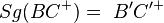Sg(BC^{+} ) = \ B'C'^{+} (2); (3); Voraussetzung; Halbgeradentreue d. GS
6) 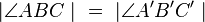\left| \angle ABC\ \right|\ =\ \left| \angle A'B'C'\ \right| (4); (5); Winkelmaßerhaltung d. GS;
7) 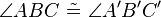\angle ABC\ \tilde {=} \ \angle A'B'C' (4); (5); (6); Winkelkongruenz

q.e.d.

--Nolessonlearned 13:27, 15. Jul. 2013 (CEST)

Der Beweis ist so nicht richtig. Es gibt keine kongruenten Halbgeraden, da wir Kongruenz von Halbgeraden nicht definiert haben (und ich auch nicht wüsste, wie man es definieren sollte). Schritt 1-3 ist lediglich eine Benennung, die aus der Def. Geradenspiegelung folgt. Schreibe Benennungen lieber in die Voraussetzung, v.a. da du diese ja bereits in der Behauptung nutzt. --Tutorin Anne 13:27, 16. Jul. 2013 (CEST)

  • Wir hatten doch mal die Halbgeradentreue bewiesen. Ich ging davon aus, dass bei der Halbgeradentreue die Halbgeraden kongruent zueinander sind.--Nolessonlearned 21:31, 16. Jul. 2013 (CEST)
    Ist nicht so, zumindest wäre mir das total neu.
    • Was muss ich mir dann unter der Halbgeradentreue vorstellen?--Nolessonlearned 12:30, 18. Jul. 2013 (CEST)

Die Halbgeradentreue besagt einfach nur : Sg (AB+) = A'B'+; Halbgeraden werden auf Halbgeraden abgebildet, sie weren nicht zur Kreisen, Wellen, Winkeln, Geraden oder sonst etwas. Das hat nichts mit dem Wort kongruent zu tun. Es gibt auch keine kongrente Geraden. --Tutorin Anne 21:02, 18. Jul. 2013 (CEST)

      • Ist vielleicht eine doofe Frage, aber warum gibt es eine Streckenkongruenz, aber keine Geraden- oder Halbgeradenkongruenz?--Nolessonlearned 21:53, 18. Jul. 2013 (CEST)
        • Gute Frage! Und die Antwort ist einfach :). Stecken und Winkel haben ein Maß. Kongruenz ist definiert über dieses Maß. Da Halbgeraden und Geraden kein Längenmaß, also keine Längenangabe haben, kann ich die Relation Kongruenz nicht brauchen.--Tutorin Anne 10:56, 19. Jul. 2013 (CEST)
Von „http://geometrie.zum.de/index.php?title=Lösung_von_Aufgabe_9.3P_(SoSe_13)&oldid=24966“