Lösung von Aufgabe 9.1P (SoSe 13): Unterschied zwischen den Versionen
(table+) |
|||
| (20 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
Beweisen Sie die Halbgeradentreue der Geradenspiegelung. Nutzen Sie für den Beweis die Streckentreue der Geradenspiegelung und eine geeignete Definition des Begriffs Halbgerade. | Beweisen Sie die Halbgeradentreue der Geradenspiegelung. Nutzen Sie für den Beweis die Streckentreue der Geradenspiegelung und eine geeignete Definition des Begriffs Halbgerade. | ||
| − | + | *Schritt 4 und 5 sind z.B. noch nicht korrekt. Strecken lassen sich nicht addieren!--[[Benutzer:Tutorin Anne|Tutorin Anne]] 21:45, 18. Jul. 2013 (CEST) | |
| Zeile 29: | Zeile 29: | ||
|} | |} | ||
--[[Benutzer:Regenschirm|Regenschirm]] 17:50, 25. Jun. 2013 (CEST) | --[[Benutzer:Regenschirm|Regenschirm]] 17:50, 25. Jun. 2013 (CEST) | ||
| − | Die Beweisidee und Schritte sind super. Es fehlen noch ein paar Striche und Klammern, damit der Beweis auch ganz richtig ist.--[[Benutzer:Tutorin Anne|Tutorin Anne]] 15:18, 26. Jun. 2013 (CEST) | + | Die Beweisidee und Schritte sind super. Es fehlen noch ein paar Striche und Klammern, damit der Beweis auch ganz richtig ist.--[[Benutzer:Tutorin Anne|Tutorin Anne]] 15:18, 26. Jun. 2013 (CEST)<br /> |
| − | + | **Darf man eigentlich <math>\overline{AP}</math> schreiben? <math>P</math> ist doch ein Vertreter aller Punkte innerhalb der Halbgerade <math>\ AB^{+</math> und diese ist ja unendlich.--[[Benutzer:Nolessonlearned|Nolessonlearned]] 14:08, 18. Jul. 2013 (CEST) | |
| + | ***Ja, das darf man. P ist ein beliebiger, aber in dem Moment wo ich ihn nenne ein fester Punkt. Und danach auch nicht mehr verschiebbar (d.h. ich kann nicht im nachhinein sagen, dass er eine bestimmte Eigenschaft erfüllt z.B. auf einer Mittelsenkrechten liegt. --[[Benutzer:Tutorin Anne|Tutorin Anne]] 21:43, 18. Jul. 2013 (CEST) | ||
<br /> | <br /> | ||
| + | ****Sorry, dass ich nochmal frage, aber in den Schritten 4 und 5 wird der Punkt zur Definition der Zwischenrelation herangezogen und wird dadurch zum festen Punkt. In Schritt 6 ist P aber wieder ein Teil der unendlichen Halbgerade. Du meintest aber, dass er im Nachhinein solche Eigenschaften nicht mehr erfüllen kann. Oder bezieht sich deine Aussage immer nur auf die Ablaufe innerhalb eines Schrittes?--[[Benutzer:Nolessonlearned|Nolessonlearned]] 22:39, 18. Jul. 2013 (CEST)<br /> | ||
| − | '''Voraussetzung''':< | + | '''Voraussetzung''': <math>\ AB^{+}\ mit\ A,B \in Ebene\ E</math><br /> |
| − | AB+ | + | |
| − | mit | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | '''Behauptung''': AB+ | + | <span style="color: red">Definitionen gehören nicht in die Voraussetzung, sondern nur die "Mitspieler". Es ist sinnvoll sich die Definitionen am Rand zu notieren und in den Begründungsschritten dann Def. ... zu schreiben, wenn man sie verwendet hat. In seltenen Fällen v.a. dann wenn es mehrere Definitionen eines Begriffs gibt, kann man die Definition dann in der Begründung auch explizit nennen. --[[Benutzer:Tutorin Anne|Tutorin Anne]] 11:47, 16. Jul. 2013 (CEST)</span><br /> |
| + | *Danke, habe die VSS geändert.--[[Benutzer:Nolessonlearned|Nolessonlearned]] 21:01, 16. Jul. 2013 (CEST)<br /> | ||
| + | '''Behauptung''': <math>Sg(AB^{+} )= A'B'^{+}</math> <br />--[[Benutzer:Nolessonlearned|Nolessonlearned]] 18:39, 14. Jul. 2013 (CEST) | ||
<br /> | <br /> | ||
| Zeile 51: | Zeile 50: | ||
|- | |- | ||
| 1) | | 1) | ||
| − | | | + | | <math>A'=Sg(A)</math> |
| − | | Eigenschaft | + | | Eigenschaft Sg |
|- | |- | ||
| 2) | | 2) | ||
| − | | | + | | <math>B'=Sg(B)</math> |
| − | | Eigenschaft | + | | Eigenschaft Sg |
|- | |- | ||
| − | | 3) | + | |3) |
| − | | <math>\ \ | + | |<math>P'=Sg(P)\ mit\ P\in Ebene\ E</math> |
| − | | | + | |Eigenschaft Sg |
|- | |- | ||
| 4) | | 4) | ||
| − | | <math>\overline{AB}\ | + | | <math>\ \overline{AB} \tilde {=} \overline{A'B'} </math> |
| − | | Voraussetzung; | + | | (1); (2); Voraussetzung; Streckentreue d. Sg |
|- | |- | ||
| 5) | | 5) | ||
| − | | <math> | + | | <math>\ AB^{+} :=\overline{AB}\ \cup\ \left\{ {P|Zw(A,B,P)} \right\}</math> |
| − | | (1); (2); (3); Voraussetzung; | + | | (1); (2); (3); Voraussetzung; Def. Halbgerade |
| − | Def. Halbgerade | + | |
|- | |- | ||
| 6) | | 6) | ||
| − | | <math> | + | | <math>\ A'B'^{+} :=\overline{A'B'}\ \cup\ \left\{ {P'|Zw(A',B',P')} \right\}</math> |
| − | | (4); (5); | + | | (1); (2); (3);(4); Voraussetzung; Def. Halbgerade; Eigenschaft Sg |
| + | |- | ||
| + | | 7) | ||
| + | | <math>Sg(AB^{+} )= A'B'^{+}</math> | ||
| + | | (4); (5); (6) | ||
q.e.d. | q.e.d. | ||
|}<br />--[[Benutzer:Nolessonlearned|Nolessonlearned]] 18:57, 14. Jul. 2013 (CEST) | |}<br />--[[Benutzer:Nolessonlearned|Nolessonlearned]] 18:57, 14. Jul. 2013 (CEST) | ||
| − | + | Schritt 6 kannst du nicht aus 4) und 5) herleiten, da eine Halbgerade ja noch aus weiteren Punkten besteht, die nicht auf der STrecke liegen. Diese könnten ja nicht aufeinander abgebildet werden. --[[Benutzer:Tutorin Anne|Tutorin Anne]] 11:47, 16. Jul. 2013 (CEST)<br /> | |
| + | * So könnte es passen.--[[Benutzer:Nolessonlearned|Nolessonlearned]] 21:01, 16. Jul. 2013 (CEST)<br /> | ||
| + | ** Du kannst die Zwischenrelation nicht einfach ersetzen. Du benötigst die Umformungsschitte, die auch im Beweis darüber zu finden sind. Nur dass da ein paar Fehler in der Schreibweise sind. --[[Benutzer:Tutorin Anne|Tutorin Anne]] 09:52, 17. Jul. 2013 (CEST)<br /> | ||
| + | ***Habe den Beweis ein wenig überarbeitet.--[[Benutzer:Nolessonlearned|Nolessonlearned]] 22:51, 18. Jul. 2013 (CEST) | ||
| + | ****Ganz ehrlich, diesen Beweis gebe ich auf. Du kannst, egal wie viel Begründungen du hinter Schritt 6 schreibst, nicht sagen, dass die Zwischenrelation auch für die Abgebildetetn Punkte gilt. Den Beweis dafür habt ihr allerdings in der Vorlesung geführt. Die Schritte müssest du dafür einfügen. Wenn du den Beweis einfach änders, korrigiere ich ihn nicht mehr! - Das ist viel zu aufwändig herauszufinden, was nun geändert wurde. --[[Benutzer:Tutorin Anne|Tutorin Anne]] 11:08, 19. Jul. 2013 (CEST) | ||
[[Kategorie:Einführung_P]] | [[Kategorie:Einführung_P]] | ||
Aktuelle Version vom 19. Juli 2013, 10:08 Uhr
Beweisen Sie die Halbgeradentreue der Geradenspiegelung. Nutzen Sie für den Beweis die Streckentreue der Geradenspiegelung und eine geeignete Definition des Begriffs Halbgerade.
- Schritt 4 und 5 sind z.B. noch nicht korrekt. Strecken lassen sich nicht addieren!--Tutorin Anne 21:45, 18. Jul. 2013 (CEST)
| Voraussetzung | 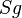 mit mit 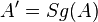 und und 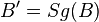 und und 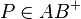
|
| Behauptung | 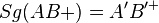 d.h. d.h. 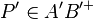
|
| Beweisschritt | Begründung |
|---|---|
1 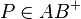 |
Voraussetzung |
2 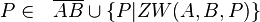 |
1), Def Halbgerade |
3 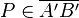 |
Streckentreue |
4 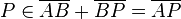 |
Def Zwischen |
5 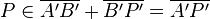 |
Abstandserhaltung der Geradenspiegelung |
6 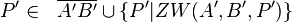 |
Def Zwischen 3), 5) |
7 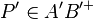 |
Def Halbgerade 6) |
--Regenschirm 17:50, 25. Jun. 2013 (CEST)
Die Beweisidee und Schritte sind super. Es fehlen noch ein paar Striche und Klammern, damit der Beweis auch ganz richtig ist.--Tutorin Anne 15:18, 26. Jun. 2013 (CEST)
- Darf man eigentlich
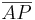 schreiben?
schreiben?  ist doch ein Vertreter aller Punkte innerhalb der Halbgerade Fehler beim Parsen(Syntaxfehler): \ AB^{+
ist doch ein Vertreter aller Punkte innerhalb der Halbgerade Fehler beim Parsen(Syntaxfehler): \ AB^{+
- Darf man eigentlich
und diese ist ja unendlich.--Nolessonlearned 14:08, 18. Jul. 2013 (CEST)
- Ja, das darf man. P ist ein beliebiger, aber in dem Moment wo ich ihn nenne ein fester Punkt. Und danach auch nicht mehr verschiebbar (d.h. ich kann nicht im nachhinein sagen, dass er eine bestimmte Eigenschaft erfüllt z.B. auf einer Mittelsenkrechten liegt. --Tutorin Anne 21:43, 18. Jul. 2013 (CEST)
- Sorry, dass ich nochmal frage, aber in den Schritten 4 und 5 wird der Punkt zur Definition der Zwischenrelation herangezogen und wird dadurch zum festen Punkt. In Schritt 6 ist P aber wieder ein Teil der unendlichen Halbgerade. Du meintest aber, dass er im Nachhinein solche Eigenschaften nicht mehr erfüllen kann. Oder bezieht sich deine Aussage immer nur auf die Ablaufe innerhalb eines Schrittes?--Nolessonlearned 22:39, 18. Jul. 2013 (CEST)
- Sorry, dass ich nochmal frage, aber in den Schritten 4 und 5 wird der Punkt zur Definition der Zwischenrelation herangezogen und wird dadurch zum festen Punkt. In Schritt 6 ist P aber wieder ein Teil der unendlichen Halbgerade. Du meintest aber, dass er im Nachhinein solche Eigenschaften nicht mehr erfüllen kann. Oder bezieht sich deine Aussage immer nur auf die Ablaufe innerhalb eines Schrittes?--Nolessonlearned 22:39, 18. Jul. 2013 (CEST)
Voraussetzung: 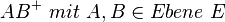
Definitionen gehören nicht in die Voraussetzung, sondern nur die "Mitspieler". Es ist sinnvoll sich die Definitionen am Rand zu notieren und in den Begründungsschritten dann Def. ... zu schreiben, wenn man sie verwendet hat. In seltenen Fällen v.a. dann wenn es mehrere Definitionen eines Begriffs gibt, kann man die Definition dann in der Begründung auch explizit nennen. --Tutorin Anne 11:47, 16. Jul. 2013 (CEST)
- Danke, habe die VSS geändert.--Nolessonlearned 21:01, 16. Jul. 2013 (CEST)
Behauptung: 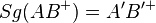
--Nolessonlearned 18:39, 14. Jul. 2013 (CEST)
| Beweisschritt | Begründung | |
|---|---|---|
| 1) | 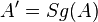
|
Eigenschaft Sg |
| 2) | 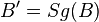
|
Eigenschaft Sg |
| 3) | 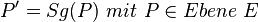
|
Eigenschaft Sg |
| 4) | 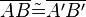
|
(1); (2); Voraussetzung; Streckentreue d. Sg |
| 5) | 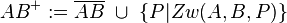
|
(1); (2); (3); Voraussetzung; Def. Halbgerade |
| 6) | 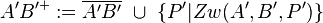
|
(1); (2); (3);(4); Voraussetzung; Def. Halbgerade; Eigenschaft Sg |
| 7) | 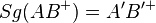
|
(4); (5); (6)
q.e.d. |
--Nolessonlearned 18:57, 14. Jul. 2013 (CEST)
Schritt 6 kannst du nicht aus 4) und 5) herleiten, da eine Halbgerade ja noch aus weiteren Punkten besteht, die nicht auf der STrecke liegen. Diese könnten ja nicht aufeinander abgebildet werden. --Tutorin Anne 11:47, 16. Jul. 2013 (CEST)
- So könnte es passen.--Nolessonlearned 21:01, 16. Jul. 2013 (CEST)
- Du kannst die Zwischenrelation nicht einfach ersetzen. Du benötigst die Umformungsschitte, die auch im Beweis darüber zu finden sind. Nur dass da ein paar Fehler in der Schreibweise sind. --Tutorin Anne 09:52, 17. Jul. 2013 (CEST)
- Habe den Beweis ein wenig überarbeitet.--Nolessonlearned 22:51, 18. Jul. 2013 (CEST)
- Ganz ehrlich, diesen Beweis gebe ich auf. Du kannst, egal wie viel Begründungen du hinter Schritt 6 schreibst, nicht sagen, dass die Zwischenrelation auch für die Abgebildetetn Punkte gilt. Den Beweis dafür habt ihr allerdings in der Vorlesung geführt. Die Schritte müssest du dafür einfügen. Wenn du den Beweis einfach änders, korrigiere ich ihn nicht mehr! - Das ist viel zu aufwändig herauszufinden, was nun geändert wurde. --Tutorin Anne 11:08, 19. Jul. 2013 (CEST)
- Habe den Beweis ein wenig überarbeitet.--Nolessonlearned 22:51, 18. Jul. 2013 (CEST)
- Du kannst die Zwischenrelation nicht einfach ersetzen. Du benötigst die Umformungsschitte, die auch im Beweis darüber zu finden sind. Nur dass da ein paar Fehler in der Schreibweise sind. --Tutorin Anne 09:52, 17. Jul. 2013 (CEST)

