Lösung von Aufgabe 12.5P (WS 13/14): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
| (4 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 16: | Zeile 16: | ||
::(4) Die Abbildung reduziert sich auf <math> S_{a'} \circ S_{d'}.</math><br> | ::(4) Die Abbildung reduziert sich auf <math> S_{a'} \circ S_{d'}.</math><br> | ||
::--[[Benutzer:EarlHickey|EarlHickey]] ([[Benutzer Diskussion:EarlHickey|Diskussion]]) 09:46, 10. Feb. 2014 (CET)<br> | ::--[[Benutzer:EarlHickey|EarlHickey]] ([[Benutzer Diskussion:EarlHickey|Diskussion]]) 09:46, 10. Feb. 2014 (CET)<br> | ||
| − | [[Kategorie:Einführung_P]] | + | <br> |
| + | 2.)<br> | ||
| + | ::Siehe Bild "Lösung_12.5b" | ||
| + | [[Datei:Lösung 12.5b.png|thumb|Lösung 12.5b]] | ||
| + | <br> | ||
| + | ::--[[Benutzer:EarlHickey|EarlHickey]] ([[Benutzer Diskussion:EarlHickey|Diskussion]]) 10:29, 10. Feb. 2014 (CET)<br> | ||
| + | 3.)<br> | ||
| + | ::Siehe ebenfalls Bild "Lösung_12.5b" | ||
| + | <br> | ||
| + | ::--[[Benutzer:EarlHickey|EarlHickey]] ([[Benutzer Diskussion:EarlHickey|Diskussion]]) 10:29, 10. Feb. 2014 (CET)<br> | ||
| + | [[Kategorie:Einführung_P]]<br /> | ||
| + | |||
| + | EarlHickey, deine Lösung hast du sehr schön dokumentiert! Echt spitze. Ergänzt werden muss nur noch die Antwort für Frage a) Du hast zwar schon die Begründung geliefert, aber die Frage noch gar nicht genau beantwortet. Handelt es sich hier um eine Drehung, Verschiebung, Punktspiegelung, Schubspiegelung ? --[[Benutzer:Tutorin Anne|Tutorin Anne]] ([[Benutzer Diskussion:Tutorin Anne|Diskussion]]) 13:48, 10. Feb. 2014 (CET)<br /> | ||
| + | Es handelt sich um eine Punktspiegelung, oder? da a´ senkrecht auf d´steht. --[[Benutzer:Smartie|Smartie]] ([[Benutzer Diskussion:Smartie|Diskussion]]) 11:44, 13. Feb. 2014 (CET) | ||
| + | * So ist es.--[[Benutzer:Tutorin Anne|Tutorin Anne]] ([[Benutzer Diskussion:Tutorin Anne|Diskussion]]) 15:17, 13. Feb. 2014 (CET) | ||
Aktuelle Version vom 13. Februar 2014, 15:17 Uhr
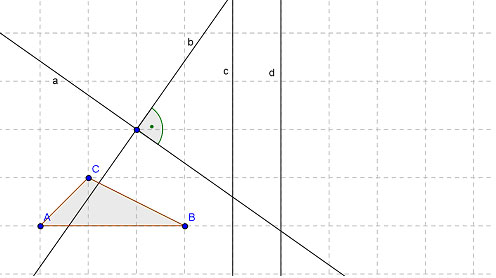
Gegeben sei ein Dreieck  und die Geraden a, b, c und d mit:
und die Geraden a, b, c und d mit: 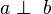 und
und 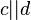 entsprechend der Skizze.
entsprechend der Skizze.
- Durch welche Abbildung kann die Verkettung der vier Geradenspiegelungen
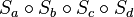 ersetzt werden (Begründen Sie Ihre Entscheidung)?
ersetzt werden (Begründen Sie Ihre Entscheidung)?
- Zeichnen Sie die Achsen der Ersatzabbildung in die Skizze oben ein. Hinweis: Sie dürfen das Gitter im Hintergrund als Orientierung nutzen.
- Konstruieren Sie oben in der Skizze das Bild des Dreiecks
 , das nach der Verkettung
, das nach der Verkettung 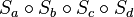 entsteht, mit Hilfe der Ersatzabbildung.
entsteht, mit Hilfe der Ersatzabbildung.
Lösung:
1.)
- (1) Drehe
 und
und  gleichsinnig um den gleichen Winkel um ihren Schnittpunkt
gleichsinnig um den gleichen Winkel um ihren Schnittpunkt  , bis
, bis  parallel zu
parallel zu  ist. | "Eig. der Drehung"
ist. | "Eig. der Drehung"
- Man erhät
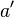 und
und 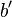 .
.
- (2) Verschiebe
 und
und  gleichsinnig und mit dem gleichen Betrag, solange bis
gleichsinnig und mit dem gleichen Betrag, solange bis  auf
auf  zu liegen kommt. | "Eig. der Geradenspiegelung
zu liegen kommt. | "Eig. der Geradenspiegelung
- Man erhät
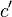 und
und 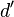 .
.
- (3) Die Geradenspiegelung an
 und
und  heben sich auf (sind involutorisch). | "Eig. der Geradenspiegelung"
heben sich auf (sind involutorisch). | "Eig. der Geradenspiegelung"
- (4) Die Abbildung reduziert sich auf
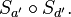
- --EarlHickey (Diskussion) 09:46, 10. Feb. 2014 (CET)
- (1) Drehe
2.)
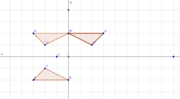
- Siehe Bild "Lösung_12.5b"
- --EarlHickey (Diskussion) 10:29, 10. Feb. 2014 (CET)
- --EarlHickey (Diskussion) 10:29, 10. Feb. 2014 (CET)
3.)
- Siehe ebenfalls Bild "Lösung_12.5b"
- --EarlHickey (Diskussion) 10:29, 10. Feb. 2014 (CET)
- --EarlHickey (Diskussion) 10:29, 10. Feb. 2014 (CET)
EarlHickey, deine Lösung hast du sehr schön dokumentiert! Echt spitze. Ergänzt werden muss nur noch die Antwort für Frage a) Du hast zwar schon die Begründung geliefert, aber die Frage noch gar nicht genau beantwortet. Handelt es sich hier um eine Drehung, Verschiebung, Punktspiegelung, Schubspiegelung ? --Tutorin Anne (Diskussion) 13:48, 10. Feb. 2014 (CET)
Es handelt sich um eine Punktspiegelung, oder? da a´ senkrecht auf d´steht. --Smartie (Diskussion) 11:44, 13. Feb. 2014 (CET)
- So ist es.--Tutorin Anne (Diskussion) 15:17, 13. Feb. 2014 (CET)