Lösung von Aufgabe 5.1 P (SoSe 14): Unterschied zwischen den Versionen
| (3 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 9: | Zeile 9: | ||
d) Die Relation ist reflexiv, sie ist nicht symmetrisch und nicht transitiv --[[Benutzer:MarieSo|MarieSo]] ([[Benutzer Diskussion:MarieSo|Diskussion]]) 19:18, 26. Mai 2014 (CEST) | d) Die Relation ist reflexiv, sie ist nicht symmetrisch und nicht transitiv --[[Benutzer:MarieSo|MarieSo]] ([[Benutzer Diskussion:MarieSo|Diskussion]]) 19:18, 26. Mai 2014 (CEST) | ||
| + | Eine Frage, was für ein Drachen ist dabei gemeint? Der schiefe Drachen ist auch ein konvexer Viereck. Wenn wir uns dann die Menge anschauen, wären noch der Parallelogramm und der Rechteck dabei. --[[Benutzer:Picksel|Picksel]] ([[Benutzer Diskussion:Picksel|Diskussion]]) 21:16, 26. Mai 2014 (CEST)<br /> | ||
| + | Das stimmt Picksel, aber es genügt mit dem symmetrischen Drachen. Zur Übung lässt sich das aber auch mit dem allgemeinen Drachen durchführen. Bis auf Antwort d) sind alle Antworten von MarieSo richtig.--[[Benutzer:Tutorin Anne|Tutorin Anne]] ([[Benutzer Diskussion:Tutorin Anne|Diskussion]]) 14:30, 31. Mai 2014 (CEST) | ||
| + | Zu d): Sie ist auch nicht reflexiv --[[Benutzer:MarieSo|MarieSo]] ([[Benutzer Diskussion:MarieSo|Diskussion]]) 13:12, 1. Jun. 2014 (CEST) | ||
| + | <br /> | ||
| + | D) Die Relation ist sehr wohl reflexiv und ebenso transitiv! Sie ist nicht symmetrisch.--[[Benutzer:Tutorin Anne|Tutorin Anne]] ([[Benutzer Diskussion:Tutorin Anne|Diskussion]]) 17:40, 2. Jun. 2014 (CEST) | ||
[[Category:Einführung_P]] | [[Category:Einführung_P]] | ||
Aktuelle Version vom 2. Juni 2014, 16:40 Uhr
a) Geben Sie die Menge 
aller konvexer Drachenvierecke an.
b) Bilden Sie das kartesische Produkt der Menge 
.
c) Wir definineren eine Relation 
mit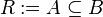 
. Bestimmen Sie die Relation auf .
d) Untersuchen Sie die Relation auf ihre Eigenschaften (reflexiv, symmetrisch, transitiv).
a) Raute (R), Quadrat (Q), Drachen (D) b) M x M : ((R,R);(R,Q);(R,D);(Q,Q);(Q,R);(Q,D);(D,D);(D,R);(D,Q)) c) R auf M x M : ((R,R);(R,D);(Q,Q);(Q,R);(Q,D);(D,D)) d) Die Relation ist reflexiv, sie ist nicht symmetrisch und nicht transitiv --MarieSo (Diskussion) 19:18, 26. Mai 2014 (CEST)
Eine Frage, was für ein Drachen ist dabei gemeint? Der schiefe Drachen ist auch ein konvexer Viereck. Wenn wir uns dann die Menge anschauen, wären noch der Parallelogramm und der Rechteck dabei. --Picksel (Diskussion) 21:16, 26. Mai 2014 (CEST)
Das stimmt Picksel, aber es genügt mit dem symmetrischen Drachen. Zur Übung lässt sich das aber auch mit dem allgemeinen Drachen durchführen. Bis auf Antwort d) sind alle Antworten von MarieSo richtig.--Tutorin Anne (Diskussion) 14:30, 31. Mai 2014 (CEST)
Zu d): Sie ist auch nicht reflexiv --MarieSo (Diskussion) 13:12, 1. Jun. 2014 (CEST)
D) Die Relation ist sehr wohl reflexiv und ebenso transitiv! Sie ist nicht symmetrisch.--Tutorin Anne (Diskussion) 17:40, 2. Jun. 2014 (CEST)
