Lösung von Aufg. 6.5P (SoSe 14): Unterschied zwischen den Versionen
| Zeile 28: | Zeile 28: | ||
|} | |} | ||
| − | Man koennte auch durch die Kontraposition Beweisen, das haben wir allerdings in der Vorlesung gemacht, als wir den Satz von Pasch bewiesen haben. <br /> | + | Man koennte auch durch die Kontraposition Beweisen, das haben wir allerdings in der Vorlesung gemacht, als wir den Satz von Pasch bewiesen haben. <br /><br /> |
| − | b) Damit haben wir die Transitivitaet bewiesen.--[[Benutzer:Picksel|Picksel]] ([[Benutzer Diskussion:Picksel|Diskussion]]) 21:03, 15. Jun. 2014 (CEST) | + | Danke für den sehr ordentlichen Beitrag. Wirklich super, Picksel!Ich würde ergänzen, von welcher Halbebenen du sprichst. Es handelt sich um die Halbebene (z.B.) <math> gA^+</math>. Dann beziehst du Schritt 4 auch auf diese Halbebene. In Schritt 5) hast du richtig gefolgert, dass A und C in der selben Halbebene liegen. In Schritt 6) genügt es zu schreiben, dass aus 5)und der Definition Halbebene folgt, dass <math>\overline{AC}\cap g=\lbrace \rbrace </math> . Damit ist der Beweis vollständig. --[[Benutzer:Tutorin Anne|Tutorin Anne]] ([[Benutzer Diskussion:Tutorin Anne|Diskussion]]) 20:25, 18. Jun. 2014 (CEST)<br /> |
| + | |||
| + | b) Damit haben wir die Transitivitaet bewiesen.--[[Benutzer:Picksel|Picksel]] ([[Benutzer Diskussion:Picksel|Diskussion]]) 21:03, 15. Jun. 2014 (CEST)<br /> | ||
| + | |||
| + | so ist es!--[[Benutzer:Tutorin Anne|Tutorin Anne]] ([[Benutzer Diskussion:Tutorin Anne|Diskussion]]) 20:25, 18. Jun. 2014 (CEST) | ||
[[Kategorie:Einführung_P]] | [[Kategorie:Einführung_P]] | ||
Aktuelle Version vom 18. Juni 2014, 19:25 Uhr
a) Gegeben seien drei paarweise verschiedene und nichtkollineare Punkte A, B und C in einer Ebene E. Ferner sei eine Gerade g Teilmenge der Ebene E, wobei keiner der Punkte A, B und C auf g liegen möge. Beweisen Sie folgenden Zusammenhang:
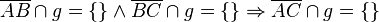
b) Was hat Aufgabe 6.5 mit Aufgabe 5.4 zu tun?
a) Direkter Beweis:
Vor.
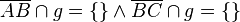
Beh.: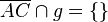 
| Nr. | Schritt | Begruendung |
|---|---|---|
| 1 |  |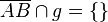
Voraussetzung |
| 2. | Punkte A und B sind auf der selben Halbebene | 1), Def. Halbebene |
| 3. |  |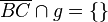
Voraussetzung |
| 4. | Punkte B und C sind auf der selben Halbebene | 3), Def. Halbebene |
| 5. | Punkte A und C sind auf der selben Halbebene, wie der Punkt B. Das heisst Punkte A und C sind auf der selben Halbebene. | 2), 4) |
| 6. | Wenn alle drei Punkte auf der selben Halbebene sind, dann schneidet weder die Strecke AB, noch BC, noch AC die Gerade g. | Schlussfolgerung aus 5) |
Man koennte auch durch die Kontraposition Beweisen, das haben wir allerdings in der Vorlesung gemacht, als wir den Satz von Pasch bewiesen haben.
Danke für den sehr ordentlichen Beitrag. Wirklich super, Picksel!Ich würde ergänzen, von welcher Halbebenen du sprichst. Es handelt sich um die Halbebene (z.B.)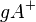 
. Dann beziehst du Schritt 4 auch auf diese Halbebene. In Schritt 5) hast du richtig gefolgert, dass A und C in der selben Halbebene liegen. In Schritt 6) genügt es zu schreiben, dass aus 5)und der Definition Halbebene folgt, dass 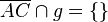. Damit ist der Beweis vollständig. --Tutorin Anne (Diskussion) 20:25, 18. Jun. 2014 (CEST)
b) Damit haben wir die Transitivitaet bewiesen.--Picksel (Diskussion) 21:03, 15. Jun. 2014 (CEST)
so ist es!--Tutorin Anne (Diskussion) 20:25, 18. Jun. 2014 (CEST)
