Lösung von Aufgabe 4.3 P (WS 14/15): Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: „a) Geben Sie die Menge <math>M</math> aller konvexer Drachenvierecke an.<br /> b) Bilden Sie das kartesische Produkt der Menge <math>M \times M</math>.<br /> c…“) |
K |
||
| (3 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 5: | Zeile 5: | ||
[[Category:Einführung_P]] | [[Category:Einführung_P]] | ||
| + | zu a) M = {s.D., D, P, Ra, Re, Q} | ||
| + | die schiefen Drachen müssen hier nicht mit rein genommen werden --[[Benutzer:Schnirch|Schnirch]] ([[Benutzer Diskussion:Schnirch|Diskussion]]) 14:22, 19. Nov. 2014 (CET) | ||
| + | |||
| + | Mit schiefen Drachen (plural) sind ja wohl sD, P und Re gemeint? --[[Benutzer:EarlHickey|EarlHickey]] ([[Benutzer Diskussion:EarlHickey|Diskussion]]) 12:26, 9. Feb. 2015 (CET)<br /> | ||
| + | <br /> | ||
| + | zu b) M x M = { '''(D,D)''', (D,Ra), (D,Q), '''(Ra,D), (Ra,Ra)''', (Ra,Q), '''(Q,D), (Q,Ra), (Q,Q)'''} | ||
| + | |||
| + | zu c) Die Relation R angewendet auf M x M, habe ich in Aufgabe b) dick markiert. | ||
| + | |||
| + | zu d) Die Relation ist reflexiv und transitiv, aber nicht symmetrisch (z.B.: Ra ist Teilmenge von D, aber D nicht Teilmenge von Ra).--[[Benutzer:Bienes|Bienes]] ([[Benutzer Diskussion:Bienes|Diskussion]]) 13:12, 21. Nov. 2014 (CET) | ||
Aktuelle Version vom 9. Februar 2015, 12:26 Uhr
a) Geben Sie die Menge 
aller konvexer Drachenvierecke an.
b) Bilden Sie das kartesische Produkt der Menge 
.
c) Wir definineren eine Relation 
mit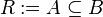 
. Bestimmen Sie die Relation auf .
d) Untersuchen Sie die Relation auf ihre Eigenschaften (reflexiv, symmetrisch, transitiv).
zu a) M = {s.D., D, P, Ra, Re, Q}
die schiefen Drachen müssen hier nicht mit rein genommen werden --Schnirch (Diskussion) 14:22, 19. Nov. 2014 (CET)
Mit schiefen Drachen (plural) sind ja wohl sD, P und Re gemeint? --EarlHickey (Diskussion) 12:26, 9. Feb. 2015 (CET)
zu b) M x M = { (D,D), (D,Ra), (D,Q), (Ra,D), (Ra,Ra), (Ra,Q), (Q,D), (Q,Ra), (Q,Q)}
zu c) Die Relation R angewendet auf M x M, habe ich in Aufgabe b) dick markiert.
zu d) Die Relation ist reflexiv und transitiv, aber nicht symmetrisch (z.B.: Ra ist Teilmenge von D, aber D nicht Teilmenge von Ra).--Bienes (Diskussion) 13:12, 21. Nov. 2014 (CET)
