Lösung von Aufgabe 4.5 P (WS 14/15): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
| Zeile 7: | Zeile 7: | ||
g schneidet g nicht und h schneidet h nicht also ist S reflexiv | g schneidet g nicht und h schneidet h nicht also ist S reflexiv | ||
Man kann g und h "tauschen" und die Relation gilt trotzdem also ist S symmetrisch | Man kann g und h "tauschen" und die Relation gilt trotzdem also ist S symmetrisch | ||
| − | h kann g schneiden und gleichzeitig kann h die gerade i schneiden, aber das heißt nicht dass g auch i schneidet. Also ist S nicht Transitiv.--[[Benutzer:Leuchtbärli|Leuchtbärli]] ([[Benutzer Diskussion:Leuchtbärli|Diskussion]]) 20:02, 24. Nov. 2014 (CET) | + | h kann g schneiden und gleichzeitig kann h die gerade i schneiden, aber das heißt nicht dass g auch i schneidet. Also ist S nicht Transitiv.--[[Benutzer:Leuchtbärli|Leuchtbärli]] ([[Benutzer Diskussion:Leuchtbärli|Diskussion]]) 20:02, 24. Nov. 2014 (CET)<br /><br /> |
| + | |||
| + | |||
| + | zur Reflexivität: Ihre Begründung stimmt nicht - überlegen Sie nochmal!--[[Benutzer:Schnirch|Schnirch]] ([[Benutzer Diskussion:Schnirch|Diskussion]]) 09:27, 25. Nov. 2014 (CET) | ||
Aktuelle Version vom 25. November 2014, 09:27 Uhr
Untersuchen Sie folgende Relation S auf ihre Eigenschaften:
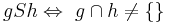
g schneidet g nicht und h schneidet h nicht also ist S reflexiv Man kann g und h "tauschen" und die Relation gilt trotzdem also ist S symmetrisch h kann g schneiden und gleichzeitig kann h die gerade i schneiden, aber das heißt nicht dass g auch i schneidet. Also ist S nicht Transitiv.--Leuchtbärli (Diskussion) 20:02, 24. Nov. 2014 (CET)
zur Reflexivität: Ihre Begründung stimmt nicht - überlegen Sie nochmal!--Schnirch (Diskussion) 09:27, 25. Nov. 2014 (CET)

