Addition von Bruchzahlen, 02.06.2015: Unterschied zwischen den Versionen
(→Übung Erweitern Kürzen) |
(→Ungleichnamige Brüche) |
||
| (2 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
=Übung Erweitern Kürzen= | =Übung Erweitern Kürzen= | ||
Aufgabe 1: Wurde richtig erweitert? | Aufgabe 1: Wurde richtig erweitert? | ||
| − | + | ||
| − | a)<math>\frac{2}{3}\<math> = <math>\frac{4}{6}\<math> | + | a) <math>\frac {2} {3} </math> = <math>\frac {4} {6} </math> |
| + | |||
| + | b) <math>\frac {7} {8} </math> = <math>\frac {9} {10} </math> | ||
| + | |||
| + | c) <math>\frac {10} {20} </math> = <math>\frac {30} {60} </math> | ||
| + | |||
| + | Schreibe alle Gleichunge auf, die richtige erweitert wurden: | ||
| + | |||
| + | ______________________________________________________________ | ||
| + | |||
| + | Aufgabe 2: Wurde richtig gekürzt? | ||
| + | |||
| + | Aufgabe 3: Wo stimmt das Gleichheitszeichen nicht? | ||
| + | |||
| + | Aufgabe 4: Erweitere... | ||
| + | a) <math>\frac {3} {8} </math> mit 5 | ||
| + | |||
| + | Aufgabe 5: Kürze... (vollständig) | ||
| + | |||
| + | Aufgabe 6: In welchen Fällen wurde mit 3 erweitert/gekürzt? | ||
| + | |||
| + | Aufgabe 7: Um welchen Faktor wurde erweitert/gekürzt? | ||
| + | |||
| + | Aufgabe 8: Fülle aus! Ergänze! | ||
| + | a) <math>\frac {7} {5} </math> = <math>\frac {x} {25} </math> | ||
| + | b) <math>\frac {x} {x} </math> = <math>\frac {x} {x} </math> | ||
| + | |||
| + | Aufgabe 9: Ordne zu. | ||
| + | |||
| + | Aufgabe 10: Erkläre in deinen Worten, was ist Erweitern/Kürzen? | ||
| + | |||
| + | oder: Lückentext: Beim Erweitern von Brüchen multipliziert man ______ und ______ mit der selben ______. | ||
=Ideen für die Einführung der Addition gebrochener Zahlen= | =Ideen für die Einführung der Addition gebrochener Zahlen= | ||
| Zeile 16: | Zeile 47: | ||
===auf symbolischer Ebene=== | ===auf symbolischer Ebene=== | ||
<math>\frac{3}{5} + \frac{4}{5}</math> | <math>\frac{3}{5} + \frac{4}{5}</math> | ||
| + | |||
| + | '''Wichtig: Darauf sensibilisieren, dass der Nenner nicht addiert wird, sondern bei gleichnamigen Brüchen gleich bleibt.''' | ||
| + | |||
==Ungleichnamige Brüche== | ==Ungleichnamige Brüche== | ||
| + | --> noch nichts abstraktes nehmen: | ||
| + | Ein Nenner ist das Vielfache vom anderen | ||
| + | |||
| + | --> wenns abstrakt wird: | ||
| + | Äquivalenzklassenkonzept | ||
Aktuelle Version vom 5. Juni 2015, 14:35 Uhr
Inhaltsverzeichnis |
Übung Erweitern Kürzen
Aufgabe 1: Wurde richtig erweitert?
a)  =
= 
b)  =
= 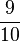
c) 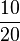 =
= 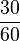
Schreibe alle Gleichunge auf, die richtige erweitert wurden:
______________________________________________________________
Aufgabe 2: Wurde richtig gekürzt?
Aufgabe 3: Wo stimmt das Gleichheitszeichen nicht?
Aufgabe 4: Erweitere...
a)  mit 5
mit 5
Aufgabe 5: Kürze... (vollständig)
Aufgabe 6: In welchen Fällen wurde mit 3 erweitert/gekürzt?
Aufgabe 7: Um welchen Faktor wurde erweitert/gekürzt?
Aufgabe 8: Fülle aus! Ergänze!
a)  =
= 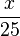 b)
b) 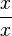 =
= 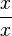
Aufgabe 9: Ordne zu.
Aufgabe 10: Erkläre in deinen Worten, was ist Erweitern/Kürzen?
oder: Lückentext: Beim Erweitern von Brüchen multipliziert man ______ und ______ mit der selben ______.
Ideen für die Einführung der Addition gebrochener Zahlen
Anfang mit gleichnamigen Brüchen
Beispielgebunden, enaktiv
- Zusammenschütten von Flüssigkeiten
- Anlegen von Strecken
...
Beispielgebunden, ikonisch
Zeichnungen
auf symbolischer Ebene
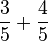
Wichtig: Darauf sensibilisieren, dass der Nenner nicht addiert wird, sondern bei gleichnamigen Brüchen gleich bleibt.
Ungleichnamige Brüche
--> noch nichts abstraktes nehmen: Ein Nenner ist das Vielfache vom anderen
--> wenns abstrakt wird: Äquivalenzklassenkonzept

