Spickzettel 2015: Unterschied zwischen den Versionen
Fli*** (Diskussion | Beiträge) |
Fli*** (Diskussion | Beiträge) |
||
| (4 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
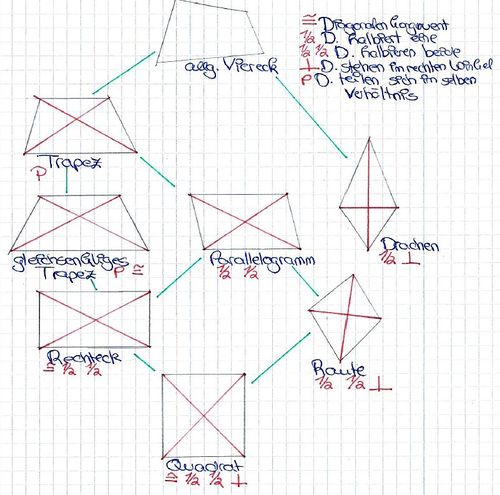
[[Bild:Haus_der_Vierecke_Diagonaleneigenschaften.JPG|mini|500px]] | [[Bild:Haus_der_Vierecke_Diagonaleneigenschaften.JPG|mini|500px]] | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | '''Absolute Geometrie''' | |
| − | + | ||
| − | - schwacher Außenwinkelsatz | + | - Umkehrung Stufenwinkelsatz - Seiten-Winkel-Beziehung a<b => α<β -schwacher Außenwinkelsatz β´ >α |
| − | + | ||
| − | + | '''Euklidische Geometrie''' | |
| − | - Wechselwinkelsatz | + | - Stufenwinkelsatz - Wechselwinkelsatz - Innenwinkelsumme im Dreieck - starker Außenwinkelsatz β´= α+γ |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
'''Scheitelwinkelsatz:''' | '''Scheitelwinkelsatz:''' | ||
| Zeile 45: | Zeile 26: | ||
'''Sätze im Dreieck''' | '''Sätze im Dreieck''' | ||
| − | Basiswinkelsatz: V: a = b := α = β | + | Basiswinkelsatz: V: a = b := α = β Wenn ein Dreieck gleichschenklig |
| + | ist, dann sind die Basiswinkel kongruent. | ||
| + | |||
'''Sätze am Kreis''' | '''Sätze am Kreis''' | ||
| Zeile 52: | Zeile 35: | ||
Zentriwinkel: Scheitelpunkt des Winkels = Mittelpunkt des Kreises | Zentriwinkel: Scheitelpunkt des Winkels = Mittelpunkt des Kreises | ||
| + | |||
| + | Peripheriewinkel sind halb so groß wie der Zentriwinkel über die selbe Sehne. | ||
Satz des Thales: V: A,B,C ɛ k und M ɛ Strecke AB := ABC ist rechtwinklig | Satz des Thales: V: A,B,C ɛ k und M ɛ Strecke AB := ABC ist rechtwinklig | ||
Aktuelle Version vom 29. Juli 2015, 17:09 Uhr
Absolute Geometrie
- Umkehrung Stufenwinkelsatz - Seiten-Winkel-Beziehung a α<β -schwacher Außenwinkelsatz β´ >α
Euklidische Geometrie
- Stufenwinkelsatz - Wechselwinkelsatz - Innenwinkelsumme im Dreieck - starker Außenwinkelsatz β´= α+γ
Scheitelwinkelsatz:
Scheitelwinkel sind kongruent.
Nebenwinkelsatz: Wenn zwei Winkel Nebenwinkel sind, dann sind sie supplementär
Seiten- Winkel- Beziehungen im Dreieck Der größeren Seite liegt der größere Winkel gegenüber
Stufenwinkelsatz (!Eukl. Geom.!) Wenn zwei Geraden a und b parallel sind, dann sind die durch einen Schnitt mit einer weiteren Geraden c entstehenden Stufenwinkel kongruent.
Sätze im Dreieck
Basiswinkelsatz: V: a = b := α = β Wenn ein Dreieck gleichschenklig ist, dann sind die Basiswinkel kongruent.
Sätze am Kreis
Peripheriewinkelsatz: Scheitelpunkt des Winkels ɛ k und die Schenkel schneiden den Kreis genau einmal → Alle Peripheriewinkel über einer Sehne sind gleich groß.
Zentriwinkel: Scheitelpunkt des Winkels = Mittelpunkt des Kreises
Peripheriewinkel sind halb so groß wie der Zentriwinkel über die selbe Sehne.
Satz des Thales: V: A,B,C ɛ k und M ɛ Strecke AB := ABC ist rechtwinklig