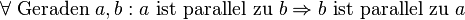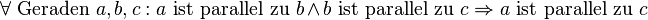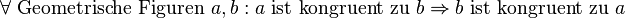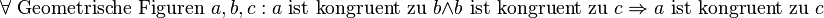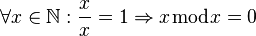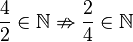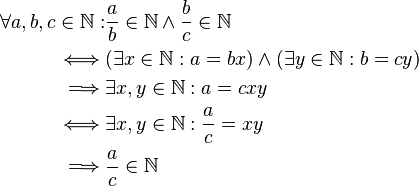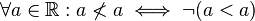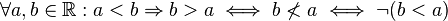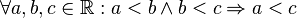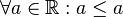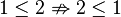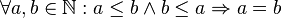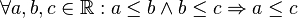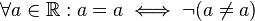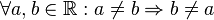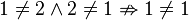Lösung von Aufgabe 5.4 P (WS 16 17): Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(Die Seite wurde neu angelegt: „Entscheiden Sie für die folgenden Relationen, ob es sich um reflexive, symmetrische sowie transitive Relationen handelt?<br /> *Parallelität von Geraden der …“)
 
 
(Eine dazwischenliegende Version von einem Benutzer wird nicht angezeigt)
Zeile 7: Zeile 7:
 
*Ungleichheit in <math>\mathbb{R}</math>
 
*Ungleichheit in <math>\mathbb{R}</math>
  
 +
<br><hr><br>
 +
 +
Zum Anzeigen die Tabelle ausklappen:
 +
<table class="wikitable sortable mw-collapsible mw-collapsed">
 +
<tr><th scope="col">Relation</th><th scope="col">Reflexiv?</th><th>Symmetrisch?</th><th>Transitiv?</th></tr>
 +
<tr>
 +
  <th>Parallelität von Geraden in der Ebene</th>
 +
  <td style="background:#afa">reflexiv<br><popup name="Begründung">Jede Gerade ist zu sich selbst parallel</popup></td>
 +
  <td style="background:#afa">symmetrisch<br><popup name="Begründung"><math>\forall\text{ Geraden }a,b: a\text{ ist parallel zu }b \Rightarrow b\text{ ist parallel zu }a</math></popup></td>
 +
  <td style="background:#afa">transitiv<br><popup name="Begründung"><math>\forall\text{ Geraden }a,b,c: a\text{ ist parallel zu }b \wedge b\text{ ist parallel zu }c \Rightarrow a\text{ ist parallel zu }c</math></popup></td>
 +
</tr>
 +
<tr>
 +
  <th>Kongruenz geometrischer Figuren</th>
 +
  <td style="background:#afa">reflexiv<br><popup name="Begründung">Jede geometrische Figur ist zu sich selbst kongruent.</popup></td>
 +
  <td style="background:#afa">symmetrisch<br><popup name="Begründung"><math>\forall\text{ Geometrische Figuren }a,b: a\text{ ist kongruent zu }b \Rightarrow b\text{ ist kongruent zu }a</math></popup></td>
 +
  <td style="background:#afa">transitiv<br><popup name="Begründung"><math>\forall\text{ Geometrische Figuren }a,b,c: a\text{ ist kongruent zu }b \wedge b\text{ ist kongruent zu }c \Rightarrow a\text{ ist kongruent zu }c</math></popup></td>
 +
</tr>
 +
<tr>
 +
  <th>Teilbarkeit in <math>\mathbb{N}</math></th>
 +
  <td style="background:#afa">reflexiv<br><popup name="Begründung"><math>\forall x \in \mathbb{N}: \frac{x}{x} = 1 \Rightarrow x \bmod x = 0</math></popup></td>
 +
  <td style="background:#faa">asymmetrisch<br><popup name="Begründung">Gegenbeispiel: <math>\frac{4}{2} \in \mathbb{N} \nRightarrow \frac{2}{4} \in \mathbb{N}</math></popup></td>
 +
  <td style="background:#afa">transitiv<br><popup name="Begründung"><math>
 +
    \begin{align}
 +
      \forall a,b,c \in \mathbb{N}: & \frac{a}{b} \in \mathbb{N} \wedge \frac{b}{c} \in \mathbb{N}\\
 +
      \iff & (\exists x\in\mathbb{N}: a=bx) \wedge (\exists y\in\mathbb{N}: b=cy)\\
 +
      \implies & \exists x,y\in\mathbb{N}: a=cxy\\
 +
      \iff & \exists x,y\in\mathbb{N}: \frac{a}{c} = xy\\
 +
      \implies & \frac{a}{c} \in \mathbb{N}
 +
    \end{align}
 +
  </math></popup></td>
 +
</tr>
 +
<tr>
 +
  <th>Kleinerrelation in <math>\mathbb{R}</math></th>
 +
  <td style="background:#faa">irreflexiv<br><popup name="Begründung"><math>\forall a \in \mathbb{R}: a \nless a \iff \neg(a<a)</math></popup></td>
 +
  <td style="background:#faa">asymmetrisch<br><popup name="Begründung"><math>\forall a,b \in \mathbb{R}: a<b \Rightarrow b>a \iff b\nless a \iff \neg(b<a)</math></popup></td>
 +
  <td style="background:#afa">transitiv<br><popup name="Begründung"><math>\forall a,b,c\in\mathbb{R}: a<b \wedge b<c \Rightarrow a<c</math></popup></td>
 +
</tr>
 +
<tr>
 +
  <th>Größer-Gleich-Relation in <math>\mathbb{R}</math></th>
 +
  <td style="background:#afa">reflexiv<br><popup name="Begründung"><math>\forall a \in \mathbb{R}: a \leq a</math></popup></td>
 +
  <td style="background:#f9f">antisymmetrisch<br><popup name="Begründung"><p>nicht symmetrisch: Gegenbeispiel <math>1\leq2\nRightarrow2\leq1</math></p><p>nicht asymmetrisch, da reflexiv</p><p>antisymmetrisch: <math>\forall a,b\in\mathbb{N}: a\leq b \wedge b\leq a \Rightarrow a=b</math></p></popup></td>
 +
  <td style="background: #afa">transitiv<br><popup name="Begründung"><math>\forall a,b,c \in\mathbb{R}: a\leq b \wedge b\leq c \Rightarrow a\leq c</math></popup></td>
 +
</tr>
 +
<tr>
 +
  <th>Ungleichheit in <math>\mathbb{R}</math></th>
 +
  <td style="background:#faa">irreflexiv<br><popup name="Begründung"><math>\forall a \in \mathbb{R}: a = a \iff \neg(a\neq a)</math></popup></td>
 +
  <td style="background:#afa">symmetrisch<br><popup name="Begründung"><math>\forall a,b \in \mathbb{R}: a\neq b \Rightarrow b\neq a</math></popup></td>
 +
  <td style="background:#faa">intransitiv<br><popup name="Begründung">Gegenbeispiel: <math>1\neq2\wedge2\neq1 \nRightarrow 1\neq1</math></popup></td>
 +
</tr>
 +
</table>--[[Benutzer:AlanTu|AlanTu]] ([[Benutzer Diskussion:AlanTu|Diskussion]]) 18:56, 15. Nov. 2016 (CET)
 +
 +
<br><hr><br>
 +
 +
Hallo AlanTu,<br />
 +
eine echt schöne und auch vollkommen richtige Tabelle hast du da erstellt, sogar mit (Gegen-)Beispielen als Begründung ;)<br />
 +
Weiter so! Gruß Alex --[[Benutzer:Tutor: Alex|Tutor: Alex]] ([[Benutzer Diskussion:Tutor: Alex|Diskussion]]) 03:19, 16. Nov. 2016 (CET)
  
  
 
[[Category:Geo_P]]
 
[[Category:Geo_P]]

Aktuelle Version vom 16. November 2016, 03:19 Uhr

Entscheiden Sie für die folgenden Relationen, ob es sich um reflexive, symmetrische sowie transitive Relationen handelt?

  • Parallelität von Geraden der Ebene
  • Kongruenz geometrischer Figuren
  • Teilbarkeit in \mathbb{N}
  • Kleinerrelation in \mathbb{R}
  • Größer-Gleich-Relation in \mathbb{R}
  • Ungleichheit in \mathbb{R}


Zum Anzeigen die Tabelle ausklappen:

RelationReflexiv?Symmetrisch?Transitiv?
Parallelität von Geraden in der Ebene reflexiv
 symmetrisch
 transitiv
Kongruenz geometrischer Figuren reflexiv
 symmetrisch
 transitiv
Teilbarkeit in \mathbb{N} reflexiv
 asymmetrisch
 transitiv
Kleinerrelation in \mathbb{R} irreflexiv
 asymmetrisch
 transitiv
Größer-Gleich-Relation in \mathbb{R} reflexiv
 antisymmetrisch
 transitiv
Ungleichheit in \mathbb{R} irreflexiv
 symmetrisch
 intransitiv
--AlanTu (Diskussion) 18:56, 15. Nov. 2016 (CET) 

Hallo AlanTu,

eine echt schöne und auch vollkommen richtige Tabelle hast du da erstellt, sogar mit (Gegen-)Beispielen als Begründung ;)

Weiter so! Gruß Alex --Tutor: Alex (Diskussion) 03:19, 16. Nov. 2016 (CET)
Von „http://geometrie.zum.de/index.php?title=Lösung_von_Aufgabe_5.4_P_(WS_16_17)&oldid=28811“