Lösung Aufgabe 2.07 SoSe 2017: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(→Lösung 1) |
*m.g.* (Diskussion | Beiträge) (→Lösung 1) |
||
| Zeile 8: | Zeile 8: | ||
==Lösung 1== | ==Lösung 1== | ||
| + | ===Lösung von Maaurtoc=== | ||
Hier wird die Primzahl definiert. | Hier wird die Primzahl definiert. | ||
| Zeile 13: | Zeile 14: | ||
<math>P</math> besteht nach Definition aus der Menge <math>p</math>, für die gilt:<br> | <math>P</math> besteht nach Definition aus der Menge <math>p</math>, für die gilt:<br> | ||
<math>p</math> ist eine Natürliche Zahl mit der Eigenschaft, dass eine andere Zahl <math>a</math> die Zahl <math>p</math> teilt und <math>a</math> entweder gleich <math>1</math> oder gleich <math>p</math> ist. | <math>p</math> ist eine Natürliche Zahl mit der Eigenschaft, dass eine andere Zahl <math>a</math> die Zahl <math>p</math> teilt und <math>a</math> entweder gleich <math>1</math> oder gleich <math>p</math> ist. | ||
| + | ===Kommentar --[[Benutzer:*m.g.*|*m.g.*]] ([[Benutzer Diskussion:*m.g.*|Diskussion]]) 12:38, 7. Mai 2017 (CEST)=== | ||
| + | Die Idee der Definition haben Sie perfekt erkannt. <br /> | ||
| + | Ihre Formulierung bzgl. <math>P</math> und <math>p</math> ist jedoch nicht ganz konsistent: | ||
| + | # Mit großen lateinischen Buchstaben werden Mengen bezeichnet. Mit <math>P</math> bezeichnen wir im konkreten Fall die Menge aller Primzahlen. <math>p</math> steht demgegenüber für eine beliebige Primzahl. <math>p</math> ist damit eine Variable, die jeweils mit einer und nur einer konkreten Zahl belegt werden darf. Merken Sie worauf ich hinaus will? | ||
==Lösung 2== | ==Lösung 2== | ||
Aktuelle Version vom 7. Mai 2017, 11:38 Uhr
Langenscheidt Mathe - DeutschÜbersetzen Sie die folgende Definition in "normales" Deutsch: Definition
Lösung 1Lösung von MaaurtocHier wird die Primzahl definiert. Übersetzt heißt das:
Kommentar --*m.g.* (Diskussion) 12:38, 7. Mai 2017 (CEST)Die Idee der Definition haben Sie perfekt erkannt.
Lösung 2 |
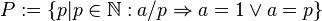
 besteht nach Definition aus der Menge
besteht nach Definition aus der Menge  , für die gilt:
, für die gilt: die Zahl
die Zahl 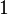 oder gleich
oder gleich 
