Lösung Aufgabe 5.01 SoSe 2017: Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(→‎Lösung 1)
 
Zeile 13: Zeile 13:
 
# Ergänzen Sie <math>\mathbb{M}</math> derart, dass alle Axiome der ebenen Inzidenz erfüllt sind.
 
# Ergänzen Sie <math>\mathbb{M}</math> derart, dass alle Axiome der ebenen Inzidenz erfüllt sind.
 
=Lösung 1=
 
=Lösung 1=
 +
Das Modell M erfüllt 2 Axiome nicht und muss somit um diese zwei erweitert werden
 +
 +
 +
1. Axiom 1.3 Es gibt wenigstens 3 verschiedene Punkte, da ohne diese Ergänzung A,B,C,D identisch sein könnten und somit keine Gerade bilden. <br>
 +
P:(A,B,C,D, (logisches und) A,B,C,(D) sind paarweise verschieden)
 +
 +
2. Axiom 1.2(kollinear) weiterhin muss in P erwähnt werden das mindestens 3 punkte nicht auf einer gemeinsamen Geraden liegen. <br> 
 +
P:(A,B,C,D, (logisches und) A,B,C,D sind paarweise verschieden ( logisches und) nkoll(A,B,C))
  
 
=Lösung 2=
 
=Lösung 2=

Aktuelle Version vom 31. Mai 2017, 17:36 Uhr

Inhaltsverzeichnis

Aufgabe 5.01 SoSe 2017

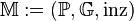Wir betrachten das folgende Modell \mathbb{M}:=(\mathbb{P}, \mathbb{G}, \operatorname{inz}) für die Inzidenzgeometrie:
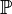Modellpunkte \mathbb{P}:
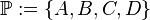
\mathbb{P} := \{A,B,C,D\}
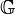Modellgeraden \mathbb{G}:
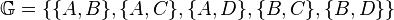
\mathbb{G} = \{\{A,B\}, \{A,C\}, \{A,D\}, \{B,C\}, \{B,D\}\}
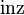Inzidenz \operatorname{inz}:
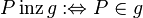
Elementbeziehung: Ein Punkt P inzidiert mit einer Geraden g , wenn er zu g gehört: P \operatorname{inz} g :\Leftrightarrow P \in g

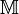  1. Warum ist \mathbb{M} kein Modell für die ebene Inzidenzgeometrie?
  2. Ergänzen Sie \mathbb{M} derart, dass alle Axiome der ebenen Inzidenz erfüllt sind.

Lösung 1

Das Modell M erfüllt 2 Axiome nicht und muss somit um diese zwei erweitert werden


1. Axiom 1.3 Es gibt wenigstens 3 verschiedene Punkte, da ohne diese Ergänzung A,B,C,D identisch sein könnten und somit keine Gerade bilden. 

P:(A,B,C,D, (logisches und) A,B,C,(D) sind paarweise verschieden)

2. Axiom 1.2(kollinear) weiterhin muss in P erwähnt werden das mindestens 3 punkte nicht auf einer gemeinsamen Geraden liegen. 

P:(A,B,C,D, (logisches und) A,B,C,D sind paarweise verschieden ( logisches und) nkoll(A,B,C))

Lösung 2

Lösung 3

Von „http://geometrie.zum.de/index.php?title=Lösung_Aufgabe_5.01_SoSe_2017&oldid=29962“