Pfeilklassen SoSe 2017: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (→Aufgabe 3 (Pfeilklassen SoSe 2017)) |
*m.g.* (Diskussion | Beiträge) |
||
| Zeile 1: | Zeile 1: | ||
| + | <div style="margin:0; margin-right:4px; border:1px solid #27408B; padding: 1em 1em 1em 1em; background-color:#B9D0F0; align:left;"> | ||
| + | {|width=90%| style="background-color:#B9D0F0; padding:1em" | ||
| + | | valign="top" | | ||
| + | <!--- hier drüber nichts eintragen ---> | ||
| + | |||
| + | |||
=Aufgabe 1 (Pfeilklassen SoSe 2017)= | =Aufgabe 1 (Pfeilklassen SoSe 2017)= | ||
In einem kartesischen Koordinatensystem mit dem Ursprung <math>O</math> seien die Punkte <math>P\left(\frac{1}{2}\sqrt{2},\frac{1}{2}\sqrt{2}\right)</math> und <math>Q \left(\frac{1}{2}\sqrt{3}, \frac{1}{2} \right)</math> gegeben.<br /> | In einem kartesischen Koordinatensystem mit dem Ursprung <math>O</math> seien die Punkte <math>P\left(\frac{1}{2}\sqrt{2},\frac{1}{2}\sqrt{2}\right)</math> und <math>Q \left(\frac{1}{2}\sqrt{3}, \frac{1}{2} \right)</math> gegeben.<br /> | ||
| Zeile 10: | Zeile 16: | ||
=Aufgabe 5 (Pfeilklassen SoSe 2017)= | =Aufgabe 5 (Pfeilklassen SoSe 2017)= | ||
Beweisen Sie: Die Pfeilklassen der Ebene bilden mit der Pfeilklassenaddition eine abelsche Gruppe. | Beweisen Sie: Die Pfeilklassen der Ebene bilden mit der Pfeilklassenaddition eine abelsche Gruppe. | ||
| + | |||
| + | <!--- hier drunter nichts eintragen ---> | ||
| + | [[Kategorie:Linalg]] | ||
| + | |||
| + | |} | ||
| + | </div> | ||
Aktuelle Version vom 4. Juni 2017, 13:48 Uhr
|
Aufgabe 1 (Pfeilklassen SoSe 2017)In einem kartesischen Koordinatensystem mit dem Ursprung Aufgabe 2 (Pfeilklassen SoSe 2017)Es sei Aufgabe 3 (Pfeilklassen SoSe 2017)Es sei Aufgabe 4 (Pfeilklassen SoSe 2017)Beweisen Sie: Aufgabe 5 (Pfeilklassen SoSe 2017)Beweisen Sie: Die Pfeilklassen der Ebene bilden mit der Pfeilklassenaddition eine abelsche Gruppe. |
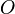 seien die Punkte
seien die Punkte 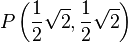 und
und 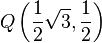 gegeben.
gegeben.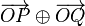 Berechnen Sie die Länge die jeder Pfeil aus
Berechnen Sie die Länge die jeder Pfeil aus  ein rechtwinkliges Dreieck mit dem rechten Winkel bei
ein rechtwinkliges Dreieck mit dem rechten Winkel bei  .
.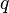 seien wie üblich die Längen der Hypotenusenabschnitte von
seien wie üblich die Längen der Hypotenusenabschnitte von 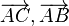 und
und 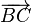 bezüglich eines Koordinatensystems, dessen Ursprung der Fußpunkt der Höhe
bezüglich eines Koordinatensystems, dessen Ursprung der Fußpunkt der Höhe 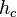 ist. Ferner gelte, dass
ist. Ferner gelte, dass  auf der positiven
auf der positiven 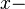 Achse und
Achse und 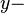 Achse liegt.
Achse liegt.
 ein Parallelogramm. Beweisen Sie:
ein Parallelogramm. Beweisen Sie: 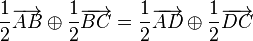 .
.
 ist auf der Menge der Pfeilklassen der Ebene repräsentantenunabhängig.
ist auf der Menge der Pfeilklassen der Ebene repräsentantenunabhängig.

