Lösung von Aufgabe 7.09 SoSe 2017: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(→Lösung 1) |
(→Lösung 1) |
||
| (Eine dazwischenliegende Version von einem Benutzer wird nicht angezeigt) | |||
| Zeile 8: | Zeile 8: | ||
=Lösung 1= | =Lösung 1= | ||
Seien A, B und C drei nicht kollineare und paarweise verschiedene Punkte. <br /> | Seien A, B und C drei nicht kollineare und paarweise verschiedene Punkte. <br /> | ||
| − | Die Strecken <math>\overline{AB},\overline{BC} \ und \ \overline{CA}</math> bilden ein Dreieck. | + | Die Strecken <math>\overline{AB},\overline{BC} \ und \ \overline{CA}</math> bilden ein Dreieck.<br /> |
| + | <br /> | ||
| + | |||
| + | Was bedeutet es, dass drei Strecken ein Dreieck bilden? Wie ist ''bilden'' definiert?<br /> | ||
| + | <br /> | ||
| + | Die Vereinigungsmenge der Strecken <math>\overline{AB},\overline{BC} \ und \ \overline{CA}</math> heißt Dreieck.<br /> | ||
| + | Ist es so korrekt? | ||
=Lösung 2= | =Lösung 2= | ||
Aktuelle Version vom 23. Juni 2017, 07:24 Uhr
|
Definieren Sie den Begriff Dreieck. Hinweis: Unter einem Dreieck versteht man seine Seiten. Lösung 1Seien A, B und C drei nicht kollineare und paarweise verschiedene Punkte. Was bedeutet es, dass drei Strecken ein Dreieck bilden? Wie ist bilden definiert? Lösung 2 |
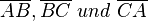bilden ein Dreieck.
