Die symmetrische Gruppe S4 WS17/18: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (→S_3) |
*m.g.* (Diskussion | Beiträge) |
||
| Zeile 1: | Zeile 1: | ||
| + | <div style="margin:0; margin-right:4px; border:1px solid #27408B; padding: 1em 1em 1em 1em; background-color:#CCFFCC; align:left;"> | ||
| + | {|width=90%| style="background-color:#CCFFCC; padding:1em" | ||
| + | | valign="top" | | ||
| + | |||
==Begriff der symmetrischen Gruppe <math>S_n</math>== | ==Begriff der symmetrischen Gruppe <math>S_n</math>== | ||
Unter einer symmetrischen Gruppe <math>S_n</math> versteht man die Gruppe aller Permutationen von <math>n</math> Elementen.<br /> | Unter einer symmetrischen Gruppe <math>S_n</math> versteht man die Gruppe aller Permutationen von <math>n</math> Elementen.<br /> | ||
| Zeile 16: | Zeile 20: | ||
[[Datei:S4 leer.png|thumb|screenshot der Exceldatei S4_leer]] | [[Datei:S4 leer.png|thumb|screenshot der Exceldatei S4_leer]] | ||
| + | |||
| + | <!--- Was hier drunter steht muss stehen bleiben ---> | ||
| + | |} | ||
| + | </div> | ||
| + | [[Kategorie:Algebra]] | ||
Aktuelle Version vom 31. Oktober 2017, 15:31 Uhr
Begriff der symmetrischen Gruppe
|
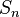
 Elementen.
Elementen.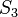
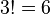 Permutationen.
Permutationen.
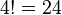 Permutationen.
Permutationen.

